Разбиение чисел

Числа Белла

Числа Стирлинга второго рода

n	k

Числа Белла определяются как сумма всех разбиений от 0 до n блоков множества n-X:

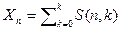. (3.34)

Первые восемь чисел Белла в таблице 3.2.

При посчете числа разбиений необходимо иметь в виду, что числа Белла растут очень быстро. Так, например, уже при n = 20 B_n = 51 724 158 235 372.

Таблица 3.2

n
Bn

Под разбиением числа n понимается его представление в виде 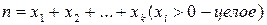. При этом порядок слагаемых не существенен, а

Суммы считаются эквивалентными, если они отличаются лишь порядком слагаемых.

Число разбиений числа n на k слагаемых будем обозначать P(n, k), число всех разбиений – P(n).

Очевидно, что

k	Разбиения n	P(n, k)
	6 1
	5 2
	4 3
	5 1 1
	4 2 1
	3 3 1
	3 2 2
	4 1 1 1
	3 2 1 1
	2 2 2 1
	3 1 1 1 1
	2 2 1 1 1
	2 1 1 1 1 1 1
	1 1 1 1 1 1 1
Рис. 3.8

Рассмотрим пример. Пусть необходимо получить все разбиения числа n =7. Это возможно сделать различными способами, показанными на рис. 3.8.

Разложение P(n) в сумму P(n, k) делает наглядной структуру разбиений числа n, однако вычисление значений P(n) непосредственно по формуле (3.36) не всегда возможно, поскольку сами значения P(n, k) заранее, как правило, не известны.

Для подсчета P(n) удобно воспользоваться функцией Q(m, n), значением которого является число способов представления целого m в виде суммы при условии, что каждое слагаемое не превосходит n. Число разбиений целого n равно Q(n, n)= P(n).

Теорема. Пусть Q(m, n) – функция, значением которой является число способов представления целого m в виде суммы при условии, что каждое слагаемое не превосходит n. Тогда функция Q(m, n) удовлетворяет следующему рекурсивному определению:

При исследовании свойств чисел P(n) могут также оказаться полезными диаграммы Феррерса. Диаграммы Феррерса состоит из k строк, соответствующих слагаемым разбиения, причем i -ая строка содержит последовательность из x_i точек.

Например, разлагая 7 на четыре слагаемых, имеем одну из диаграмм Феррерса.

7=3+2+1+1

Каждому разбиению, изображенному диаграммой Феррерса соответствует сопряженное разбиение, которое получается заменой строк столбцами.

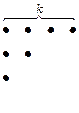7=4+2+1

Непосредственно из определения диаграммы Феррерса следует, что число разбиений числа n на k слагаемых равно числу разбиений числа n с наибольшим слагаемым, равным k.

Получим алгоритм генерирования всех разбиений числа n.

Пусть Обозначим 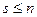такое, что

,

где

Для построения этого алгоритма достаточно заметить, что разбиение s’, непосредственно следующее за s, имеет вид

где символами [s/j] обозначено наибольшее целое, не превосходящее s/j.

При этом все элементы разбиения являются общими как для s, так и для s’.

Инициация алгоритма осуществляется значениями i =1, a_i=n, j=n -1, k =1.

Дата добавления: 2014-01-07