Нормальные делители

Пусть G – произвольная группа, а H – подгруппа группы G, тогда, если 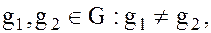то мы получаем два левых смежных класса 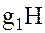и .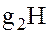

Мы хотим выяснить условия, при которых произведение элементов, взятых из смежных классов 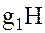и 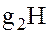, не зависит от выбора представителей классов и всегда принадлежит одному и тому же смежному классу, что и произведение элементов 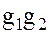, а именно классу .

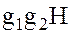Элемент 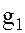принадлежит смежному классу 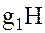, а элемент 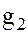– смежному классу .

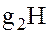Произвольные элементы, принадлежащие, соответственно, смежным классам 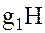и 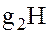можно представить в виде:

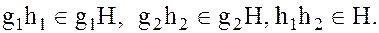
Тогда их произведение

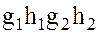
должно принадлежать классу

.

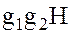Это означает, что в подгруппе H,

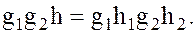
Умножая почленно полученное равенство слева на 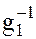, имеем:

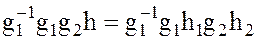
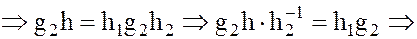
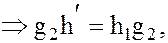(9)

где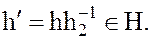

Соотношение (9) позволяет сделать следующий вывод.

Так как элементы выбраны произвольно, то для любого элемента и любого элемента 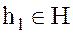существует элемент

,

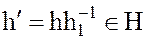удовлетворяющий соотношению (9).

Кроме того, элемент 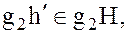а элемент 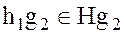. В силу этого каждый левый смежный класс группы G по H содержится в некотором правом смежном классе группы G по той же подгруппе H:

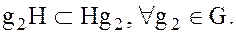
Аналогично можно показать и обратное включение

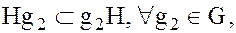
а это будет означать, что

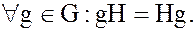(10)

Определение 1. Подгруппа H группы G называется нормальным делителем или инвариантной подгруппой, если для любых двух смежных классов g₁H и g₂H по подгруппе H, произведение 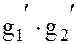произвольных элементов 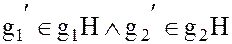из этих классов, принадлежит одному и тому же смежному классу 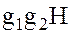(рис. 2).

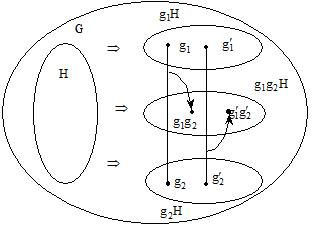
Рис. 2 – Подгруппа H – нормальный делитель группы G.

Формально: подгруппа H – нормальный делитель группы 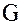, если:

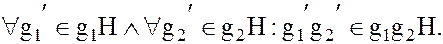(11)

В коммутативных группах всякая подгруппа является нормальным делителем (в силу коммутативности операции сложения).

Для практического использования понятия нормального делителя рассмотрим еще несколько более «конструктивных в обращении» определений.

Определение 2. Подгруппа H группы G является нормальным делителем группы G в том и только том случае, если каждый левый смежный класс 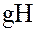совпадает с правым смежным классом 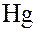группы G по H и наоборот.

Формально: подгруппа H – нормальный делитель группы G, если:

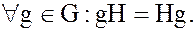(12)

Условие (12), очевидно, означает, что:

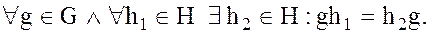
Примеры.

1. В любой группе G сама группа 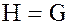и единичная подгруппа 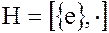являются ее нормальными делителями: левый и правый смежные классы группы G по подгруппе 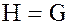состоит из одного смежного класса 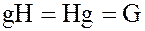, а левый (правый) смежные классы по единичной подгруппе H состоят из всех элементов группы G.

2. В каждой абелевой группе G каждая ее подгруппа H является нормальным делителем.

3. Мультипликативная группа положительных вещественных чисел 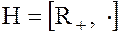является нормальным делителем мультипликативной группы всех отличных от нуля вещественных чисел,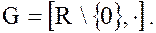

4. Мультипликативная группа отличных от нуля рациональных чисел 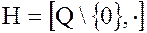является нормальным делителем мультипликативной группы отличных от нуля вещественных чисел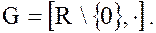

5. В мультипликативной группе 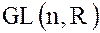невырожденных матриц 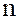-го порядка с вещественными коэффициентами подгруппа 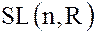матриц с определителем равным единице:

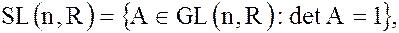
является нормальным делителем этой группы.

Действительно, единичная матрица 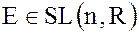, если

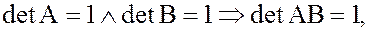
кроме того

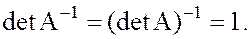
Далее, если 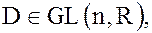то

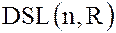и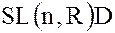

– соответственно, левый и правый смежные классы группы 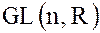-невырожденных матриц 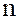-го порядка с вещественными коэффициентами по подгруппе - матриц с определителем равным единице.

Если

,

т.е.

,

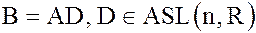то

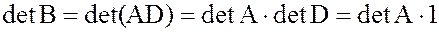, т.е. .

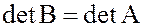С другой стороны, если

,

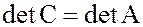то

поскольку 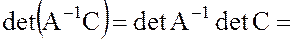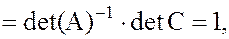поэтому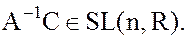

Следовательно, сгруппировав в один смежный класс (левый или правый) все матрицы с равными детерминантами, получим разложение группы 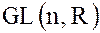по подгруппе 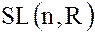.Этот пример показывает, что и в некоммутативных группах могут быть подгруппы – нормальные делители, для которых левый смежный класс

совпадает с правым смежным классом

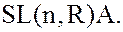
Дата добавления: 2014-01-07