Сопряжённые элементы

Пусть

Определение. Элементы 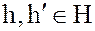называются сопряженными, если

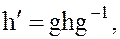(13)

а элемент h получается из 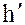трансформированием элемента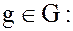

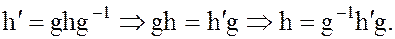(14)

Определение 3. Подгруппа H группы G является нормальным делителем группы G в том и только том случае, если для любого элемента g группы G вместе со всяким своим элементом 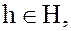она содержит и сопряженный ему элемент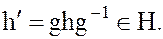

Формально: подгруппа H – нормальный делитель группы G, если:

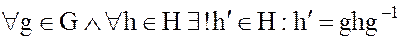. (15)

Используя это определение, легко доказать следующую теорему.

Теорема. Пересечение 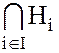любого семейства нормальных делителей группы G является нормальным делителем этой группы.

Доказательство. Пусть 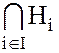– пересечение некоторого семейства нормальных делителей группы G. Как было доказано ранее, пересечение подгрупп 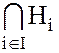группы G, есть подгруппа группы G.

Если то h принадлежит всем нормальным делителям 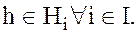Поэтому каждый элемент 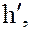сопряженный с элементом h, также принадлежит каждой из подгрупп 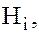а следовательно, он принадлежит и их пересечению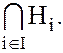

Понятие сопряженного элемента для подгруппы H, являющейся нормальным делителем группы G, позволяет дать изящное доказательство и следующей теореме.

Теорема. Ядро гомоморфизма 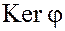является нормальным делителем в группе G.

Доказательство. Пусть 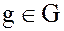– произвольный, но фиксированный элемент группы G.

Тогда 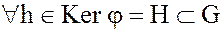найдем сопряженный ему элемент

.

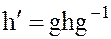Необходимо показать, что он так же принадлежит .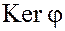

Действительно, так как 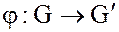– изоморфизм, то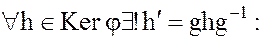

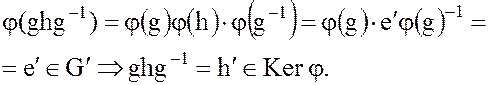
Это означает, что подгруппа 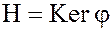группы G содержит вместе со всяким своим элементом 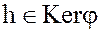и сопряженные ему элемент 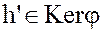и, следовательно, 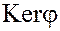является нормальным делителем в G.

Дата добавления: 2014-01-07