
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод фазовых портретов
|
|
|
|
Дифференциальное уравнение системы автоматического управления может быть преобразовано в систему n дифференциальных уравнений 1-го порядка
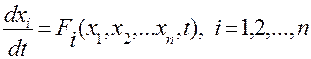 (7.1)
(7.1)
с начальными условиями xi(0). Величины xi(t) можно рассматривать как координаты некоторой точки М, называемой изображающей точкой, в n – мерном пространстве. Изображающая точка при изменении координат описывает в этом пространстве некоторую кривую, которая называется фазовой траекторией. Совокупность фазовых траекторий, полученных при различных начальных условиях, называется фазовым портретом системы. Наглядное представление фазовых траектория возможно только для систем, порядок которых не выше второго, или для систем, которые могут быть сведены к системам второго порядка. Исследование поведения нелинейных систем, ниже излагаемым методом, возможно только для автономных стационарных систем. Система является автономной, если ее правая часть явно не зависит от времени.
Уравнение автономной системы 2-го порядка можно записать в виде
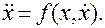 (7.2)
(7.2)
Полагая  получим
получим
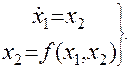 (7.3)
(7.3)
Фазовыми координатами являются выходная переменная системы x1 и скорость ее изменения x2. Разделим второе уравнение системы на первое и получим дифференциальное уравнение фазовых траекторий
 (7.4)
(7.4)
Уравнение (7.4) однозначно определяет касательную к фазовой траектории во всех точках, кроме тех, в которых одновременно выполняются равенства
 (7.5)
(7.5)
В этих точках, которые называются особыми точками, не существует определенного направления касательной к траектории. В особых точках фазовые координаты равны нулю, следовательно, в этих точках система находится в положении равновесия. Для определения особых точек необходимо решить систему (7.5).
|
|
|
Выясним характер особых точек и оценим устойчивость положения равновесия системы в окрестности этих точек. Пусть x1(0) и x2=0 есть координаты особой точки. Линеаризуем систему (7.3) в окрестности особой точки, полагая
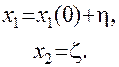
Тогда
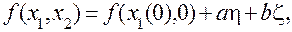 (7.6)
(7.6)
где 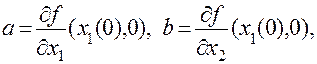 с точностью до малых не выше первого порядка малости. Подставим выражение (7.6) в (7.3) и, принимая во внимание, что координаты особой точки удовлетворяют уравнениям (7.5), получим систему уравнений первого приближения
с точностью до малых не выше первого порядка малости. Подставим выражение (7.6) в (7.3) и, принимая во внимание, что координаты особой точки удовлетворяют уравнениям (7.5), получим систему уравнений первого приближения
 (7.7)
(7.7)
Решив эту систему уравнений, можно определить движение линеаризованной системы и ее фазовые траектории вблизи особой точки и оценить устойчивостьположения равновесия. Нужно сразу сказать, что особых точек может быть несколько и судить об устойчивости каждого такого положения равновесия по линеаризованным уравнениям можно только в малом, т.е. при малых отклонениях координат изображающей точки от него. Если при этих малых отклонениях фазовые координаты системы стремятся к особой точке или остаются в непосредственной близости от нее, то данное положение равновесия устойчиво и область отклонений, при которых это утверждение справедливо, называется областью притяжения рассматриваемой особой точки.
Системе (7.7) соответствует характеристическое уравнение
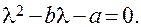 (7.8)
(7.8)
Движение системы вблизи от особой точки определяется типом корней уравнения (7.8).
1). Корни комплексно – сопряженные: l=h ± jw. Решение системы имеет в этом случае вид
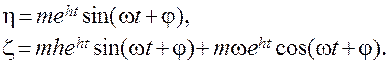
Здесь m и j - постоянные интегрирования, определяемые начальными условиями. Изображающая точка стремиться к началу координат (особой точке) при t®¥, если h< 0, и удаляется от него, если h> 0. Фазовыя траектории для таких случаев приведены на рис. 7.2а и 7.2б. Особая точка токого рода называется фокусом. При h< 0 имеет место устойчивый фокус, при h> 0 – неустойчивый фокус.
2). Корни вещественные одного знака. Решение системы (7.7) имеет вид
|
|
|
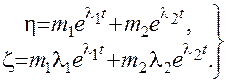 (7.9)
(7.9)
Движение является апериодическим. Изображающая точка асимптотически приближается к особой точке, если l1 и l2 отрицательны, и удаляются от нее, если l1 и l2 положительны. В частных случаях, когда m2 = 0, из (7.9) получим
 (7.10)
(7.10)
а когда m1 = 0,
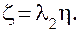 (7.11)
(7.11)
Уравнения (7.10) и (7.11) определяют прямые, по которым движется изображающая точка в указанных случаях. Чтобы получить уравнение фазовых траекторий в общем случае, исключим из уравнений (7.9) время t. Для этого умножим первое уравнение сначала на l1 и вычтем из второго, а затем умножим первое уравнение на l2 и снова вычтем его из второго. В результате получим
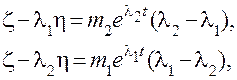
откуда, исключая t путем логарифмирования, находим уравнение фазовых траекторий в виде
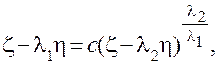 (7.12)
(7.12)
где
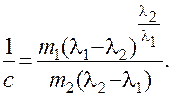 (7.13)
(7.13)
Определив из уравнения производную dz /dh в особой точке, можно убедиться, что все фазовые траектории касаются в особой точке той из прямых (7.10) и (7.11), которая соответствует меньшему по абсолютной величине из корней характеристического уравнения. Фазовые траектории, соответствующие этому случаю показаны на рис.7.2в и рис.7.2г. Особая точка такого типа называется узлом. Если корни характеристического уравнения отрицательны, то имеет место устойчивый узел, если корни положительны – неустойчивый узел.
3). Корни чисто мнимые: l = ±jw. Решение системы (7.7) имеет вид
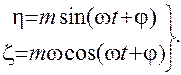 (7.14)
(7.14)
Из (7.14) нетрудно получить уравнение фазовых траекторий
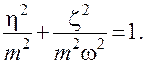 (7.15)
(7.15)
Это уравнение определяет семейство эллипсов с полуосями m и mw (рис.7.2д).
Такая особая точка называется центром. Такие фазовые траектории определяют наличие в системе незатухающих гармонических колебаний, т.е. соответствуют предельному циклу. Дальнейшие исследования заключаются в оценке устойчивости каждого предельного цикла. Если предельный цикл устойчив, то в системе происходят автоколебания. Если система имеет несколько предельных циклов, соответствующих одной и той же особой точке, то неустойчивые и устойчивые предельные циклы всегда чередуются.
4). Корни вещественные, различных знаков (l1< 0, l2> 0). Прямые (7.10) и (7.11) являются в данном случае асимптотами для фазовых траекторий. Т.к. l2> 0, то где бы не находилась изображающая точка точка в начальный момент, в конечном итоге она всегда будет удаляться от положения равновесия. Исключение составляет случай движения точно по асимптоте, но при малейшем отклонении от нее изображающая точка начнет удаляться от положения равновесия. Такая особая точка называется седлом, она всегда соответствует положению неустойчивого равновесия. Фазовые траектории такого типа приведены на рис. 7.2е. Таким образом, сутью данного метода является выделение особых точек, построение фазовых траекторий и исследование фазового портрета системы с целью определения областей устойчивости и областей притяжения устойчивых предельных циклов. Статическая характеристика нелинейного звена делит плоскость на участки, где дифференциальные уравнения системы имеют различный вид. Указанная характеристика называется, с этой точки зрения линией переключения.
|
|
|

 z z
z z
 | |||
 | |||
М(0)
 |

 h h
h h

 М(0)
М(0)
а) б)
 |






 z z
z z

 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 |  | ||||||||||||||
 | |||||||||||||||
 | |||||||||||||||











 h h
h h
 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
 | |||||||||||||||
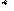 | |||||||||||||||
 | 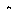 | ||||||||||||||
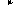 | |||||||||||||||
в) г)

 z z
z z
 | |||
 | |||
h 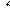





 h
h
 | |||
 | |||
д) е)
Рис. 7.2. Типы особых точек фазовой плоскости
Поэтому при построении фазовых траекторий необходимо помнить, что при переходе через линию переключения конечные значения переменных предыдущего участка являются начальными условиями для последующего участка.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1398; Нарушение авторских прав?; Мы поможем в написании вашей работы!