
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кольцо многочленов
Кольцо классов вычетов
Важнейшие типы колец
Пусть 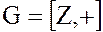 – аддитивная группа целых чисел, а
– аддитивная группа целых чисел, а 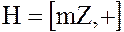 – подгруппа целых чисел, делящихся на
– подгруппа целых чисел, делящихся на 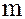 без остатка.
без остатка.
Ранее мы показали, что разбиение группы 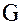 по подгруппе
по подгруппе 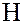 определяет фактор-множество
определяет фактор-множество
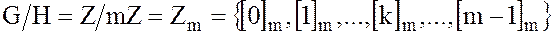 , (14)
, (14)
элементы которого 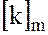 являются классы вычетов по модулю
являются классы вычетов по модулю 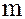 или левые смежные классы аддитивной группы целых чисел
или левые смежные классы аддитивной группы целых чисел 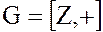 по подгруппе
по подгруппе  где
где 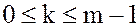 .
.
На множестве 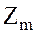 – классов вычетов по модулю
– классов вычетов по модулю 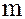 определены операции сложения
определены операции сложения 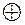 и умножения по модулю
и умножения по модулю 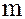 :
:
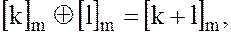 (15)
(15)
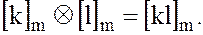 (16)
(16)
Так как выполнение этих операций сводится к соответствующим операциям над числами из классов вычетов, т.е. над элементами из 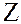 m, то
m, то 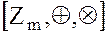 будет коммутативным кольцом с единицей
будет коммутативным кольцом с единицей  .
.
Определение. Кольцо 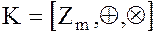 называется кольцом классов вычетов по модулю m.
называется кольцом классов вычетов по модулю m.
Вводя обозначения 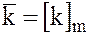 при фиксированном m, операции сложения и умножения можно записать в сокращённой форме:
при фиксированном m, операции сложения и умножения можно записать в сокращённой форме:
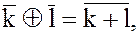 (17)
(17)
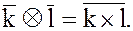 (18)
(18)
При записи операций сложения и умножения на классе вычетов по модулю 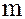 можно отказаться и от чёрточек и кружочков и оперировать с каким-либо фиксированным множеством представителей классов вычетов по модулю m.
можно отказаться и от чёрточек и кружочков и оперировать с каким-либо фиксированным множеством представителей классов вычетов по модулю m.
Чаще всего в качестве такого множества представителей выступает множество  , – которое называется приведённой системой вычетов по модулю m.
, – которое называется приведённой системой вычетов по модулю m.
Пусть 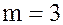 , тогда таблицы Кэли для операций сложения и умножения в кольце
, тогда таблицы Кэли для операций сложения и умножения в кольце  имеют вид:
имеют вид:

| × | |||||||
Кольцо  классов вычетов по модулю
классов вычетов по модулю 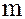 играет в алгебре важную роль и служит отправным пунктом для многочисленных обобщений.
играет в алгебре важную роль и служит отправным пунктом для многочисленных обобщений.
Пусть K – некоторое коммутативное кольцо.
Определение. Стандартным многочленом (или полиномом) степени 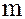 от переменной x над коммутативным кольцом K называется выражение вида
от переменной x над коммутативным кольцом K называется выражение вида
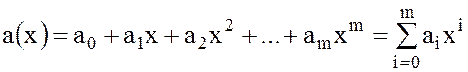 , (23)
, (23)
где 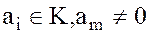 .
.
Элементы 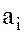 называются коэффициентами многочлена. Все они, или часть из них, могут быть нулевыми.
называются коэффициентами многочлена. Все они, или часть из них, могут быть нулевыми.
Каноническая форма многочлена (7) определяется следующим образом.
Находим наибольшее 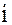 , такое, что
, такое, что 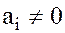 , скажем
, скажем 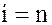 и запишем
и запишем
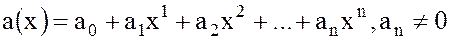 (24)
(24)
Степенью многочлена 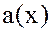 называется это число
называется это число 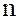 , если оно существует. Если же все
, если оно существует. Если же все 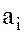 обращаются в нуль, то канонической формой многочлена является 0, а его степень –
обращаются в нуль, то канонической формой многочлена является 0, а его степень –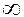 . Степень
. Степень 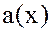 обозначается
обозначается 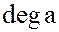 .
.
Пусть 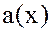 и
и 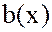 - два многочлена.
- два многочлена.
В зависимости от того, какому из множеств принадлежат коэффициенты 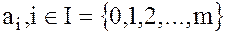 , различаются следующие типы многочленов:
, различаются следующие типы многочленов:
· с булевыми коэффициентами  ;
;
· с целочисленными коэффициентами  ;
;
· с вещественными коэффициентами 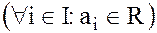 ;
;
· с рациональными коэффициентами 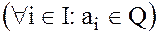 ;
;
· с комплексными коэффициентами  .
.
Лемма. Многочлены 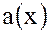 и
и  равны тогда и только тогда, когда
равны тогда и только тогда, когда 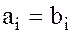
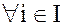 , при которых
, при которых 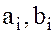 определены, а все остальные
определены, а все остальные 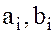 , равны нулю.
, равны нулю.
Пусть имеется два многочлена 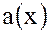 степени
степени  и
и  степени
степени 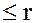 .
.
Определение. Суммой многочленов 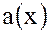 и
и  называется многочлен
называется многочлен
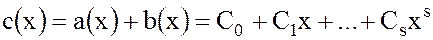 (25)
(25)
где 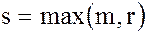 и
и
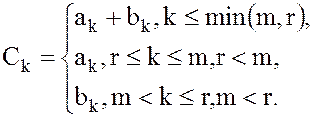 (26)
(26)
Определение. Произведением двух многочленов 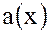 и
и  называется многочлен
называется многочлен
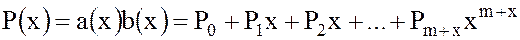 , (27)
, (27)
где 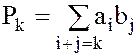 .
.
Пример. Пусть заданы два многочлена с булевыми коэффициентами т.е. 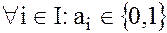 .
.
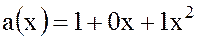
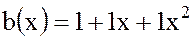
Суммой многочленов  является многочлен
является многочлен 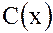 вида:
вида:
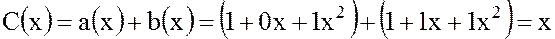 ,
,
а произведением – многочлен 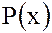 :
:
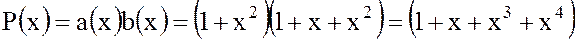
Можно показать, что введенная операция умножения многочленов ассоциативна, следовательно многочлены образуют по операции умножения полугруппу, и эта полугруппа коммутативна.
Вывод. Многочлены с целочисленными коэффициентами образуют коммутативное кольцо. Можно показать, что многочлены с рациональными, вещественными и комплексными коэффициентами также образуют соответствующие кольца многочленов. В общем случае говорят о «кольцах многочленов 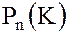 над кольцом
над кольцом 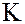 .
.
|
Дата добавления: 2014-01-07; Просмотров: 573; Нарушение авторских прав?; Мы поможем в написании вашей работы!