
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приближенное решение нелинейных интегральных уравнений методом механических квадратур
|
|
|
|
§1. Вращение вполне непрерывного векторного поля
Вращение – это целочисленная топологическая характеристика векторных полей на границах ограниченных областей.
Пусть  - ограниченная область в n -мерном пространстве
- ограниченная область в n -мерном пространстве  ; S – граница
; S – граница  . Пусть на S задано непрерывное векторное поле
. Пусть на S задано непрерывное векторное поле  без нулевых векторов. Тогда определено непрерывное отображение
без нулевых векторов. Тогда определено непрерывное отображение  границы S области
границы S области  на единичную сферу
на единичную сферу  пространства
пространства  . Степень этого отображения называют вращением поля
. Степень этого отображения называют вращением поля 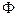 на S и обозначают его через
на S и обозначают его через 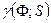 .
.
Векторное поле  называется вполне непрерывным, если A – вполне непрерывный оператор в банаховом пространстве E.
называется вполне непрерывным, если A – вполне непрерывный оператор в банаховом пространстве E.
Пусть  - ограниченная область в E, S – граница
- ограниченная область в E, S – граница  . Пусть вполне непрерывное векторное поле
. Пусть вполне непрерывное векторное поле  задано на S и не имеет на S нулевых векторов; тогда говорят, что поле
задано на S и не имеет на S нулевых векторов; тогда говорят, что поле  невырождено на S.
невырождено на S.
Обозначим через 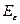 конечномерное подпространство пространства E, содержащее некоторую
конечномерное подпространство пространства E, содержащее некоторую  сеть
сеть 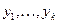 компактного множества AS. Положим
компактного множества AS. Положим

где

Нелинейный оператор  определен на AS и проектирует это компактное множество на
определен на AS и проектирует это компактное множество на 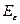 . Легко видеть, что
. Легко видеть, что  Через
Через 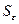 обозначим границу пересечения
обозначим границу пересечения 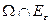 , а через
, а через  - вращение конечномерного (в пространстве
- вращение конечномерного (в пространстве 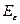 ) поля
) поля  на
на 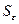 . Если
. Если 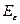 не имеет общих точек с
не имеет общих точек с  , то положим
, то положим 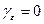 .
.
При достаточно малых  (при
(при 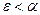 , где
, где  ) числа
) числа  одинаковы – они не зависят ни от
одинаковы – они не зависят ни от  , ни от выбора
, ни от выбора  сети, ни от выбора содержащего эту сеть подпространства. Общее значение чисел
сети, ни от выбора содержащего эту сеть подпространства. Общее значение чисел  называют вращением вполне непрерывного поля
называют вращением вполне непрерывного поля  на S и обозначают (как и в конечномерном случае) через
на S и обозначают (как и в конечномерном случае) через 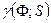 .
.
Пусть теперь  - непустое открытое ограниченное множество в вещественном банаховом пространстве F,
- непустое открытое ограниченное множество в вещественном банаховом пространстве F,  - его граница. Пусть A – вполне непрерывный на
- его граница. Пусть A – вполне непрерывный на  оператор в F, не имеющий на
оператор в F, не имеющий на  неподвижных точек. Справедливы следующие утверждения.
неподвижных точек. Справедливы следующие утверждения.
1. Если  , то уравнение
, то уравнение  имеет в
имеет в  хотя бы одно решение.
хотя бы одно решение.
|
|
|
2. Пусть B – другой вполне непрерывный на 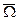 оператор в F такой, что
оператор в F такой, что

Тогда 
Отметим, что  . Действительно, в противном случае найдется такая последовательность
. Действительно, в противном случае найдется такая последовательность  , что
, что  при
при  . Ввиду полной непрерывности A можно считать, что последовательность
. Ввиду полной непрерывности A можно считать, что последовательность  сходится к некоторому пределу z. Но тогда к тому же пределу сходится последовательность
сходится к некоторому пределу z. Но тогда к тому же пределу сходится последовательность 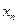 , и получаем, что
, и получаем, что  ,
,  , т.е. A имеет на
, т.е. A имеет на  неподвижную точку, вопреки условию.
неподвижную точку, вопреки условию.
3. Пусть  , где
, где  - замкнутое подпространство F. Тогда
- замкнутое подпространство F. Тогда  , где
, где  - сужение A на подпространство
- сужение A на подпространство  , а
, а 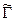 - граница множества
- граница множества  в
в  . (Может случиться, что
. (Может случиться, что 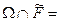 Ø. В этом случае
Ø. В этом случае 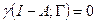 и утверждение остается в силе, если по определению положить
и утверждение остается в силе, если по определению положить  Ø)=0.)
Ø)=0.)
4. Пусть 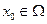 - решение уравнения
- решение уравнения  , единственное в шаре
, единственное в шаре 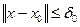 , полностью содержащемся в
, полностью содержащемся в  . Обозначим через
. Обозначим через 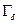 сферу
сферу  . Тогда
. Тогда  при любом
при любом 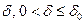 .
.
Это общее значение вращений  называется индексом изолированного решения
называется индексом изолированного решения  .
.
5. Пусть 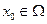 - решение уравнения
- решение уравнения  . Пусть оператор A дифференцируем по Фреше в точке
. Пусть оператор A дифференцируем по Фреше в точке  и линейный оператор
и линейный оператор  обратим. Тогда
обратим. Тогда  - изолированное решение ненулевого индекса; более того,
- изолированное решение ненулевого индекса; более того,  .
.
6. Пусть область  выпукла. Пусть A преобразует в себя замыкание
выпукла. Пусть A преобразует в себя замыкание 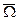 области
области  . Тогда из принципа Шаудера вытекает, что уравнение
. Тогда из принципа Шаудера вытекает, что уравнение  имеет в
имеет в 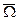 по крайней мере одно решение. Если A не имеет на
по крайней мере одно решение. Если A не имеет на  неподвижных точек, то
неподвижных точек, то  .
.
§2. Метод механических квадратур для нелинейных интегральных уравнений
Будем ссылаться на общую теорию приближенных методов для нелинейных уравнений второго рода (лекция 8).
Теорема 1. Пусть операторы T и 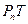 вполне непрерывны на
вполне непрерывны на 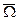 как операторы в E,
как операторы в E,  - на
- на 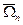 как оператор в
как оператор в 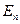 , причем
, причем
 (1)
(1)
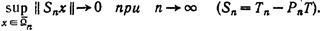 (2)
(2)
Пусть уравнение  не имеет на границе
не имеет на границе  множества
множества  решений и
решений и
 (3)
(3)
Тогда при достаточно больших n множество  решений
решений 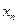 уравнения
уравнения  в
в  непусто и
непусто и

где 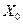 - множество решений уравнения
- множество решений уравнения  в
в  .
.
Множество 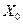 непусто в силу предположения (3).
непусто в силу предположения (3).
Следствием из теоремы 1 является
Теорема 2. Пусть операторы T и 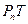 вполне непрерывны на шаре
вполне непрерывны на шаре  , а
, а  - на пересечении этого шара с
- на пересечении этого шара с 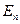 . Пусть
. Пусть  - изолированное решение уравнения
- изолированное решение уравнения  ненулевого индекса, единственное в указанном шаре. Пусть выполнены условия (1) и (2), в которых
ненулевого индекса, единственное в указанном шаре. Пусть выполнены условия (1) и (2), в которых 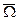 и
и 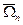 - указанные выше шар и его пересечение с
- указанные выше шар и его пересечение с 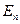 .
.
|
|
|
Тогда найдется такое 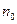 , что при
, что при 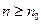 уравнение
уравнение  имеет в шаре
имеет в шаре 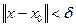 хотя бы одно решение
хотя бы одно решение 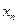 и любая последовательность таких решений
и любая последовательность таких решений 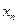 стремится при
стремится при  по норме к
по норме к  .
.
Утверждение 7. Пусть банахово пространство  непрерывно вложено в E (т.е.
непрерывно вложено в E (т.е.  ,
, 
 ). Пусть оператор T переводит
). Пусть оператор T переводит 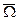 в компактное в
в компактное в 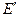 подмножество, а проекторы
подмножество, а проекторы  ограничены как операторы из
ограничены как операторы из 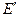 в E, причем
в E, причем  сильно, где P – оператор вложения пространства
сильно, где P – оператор вложения пространства 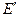 в E. Тогда выполняется условие (1).
в E. Тогда выполняется условие (1).
Рассмотрим нелинейное интегральное уравнение
 (4)
(4)
с непрерывным ядром  и непрерывным свободным членом
и непрерывным свободным членом  . Приближенные значения
. Приближенные значения 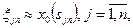 искомого решения
искомого решения  определяем из системы уравнений
определяем из системы уравнений
 (5)
(5)
Эта система выведена на основе квадратурной формулы
 . (6)
. (6)
Предполагаем, что  , и узлы интерполяции
, и узлы интерполяции
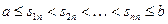 .
.
Теорема 3. Пусть квадратурный процесс (6) сходится, т.е.  при
при  для любой непрерывной на
для любой непрерывной на  функции
функции  . Пусть уравнение (4) имеет решение
. Пусть уравнение (4) имеет решение  , и пусть ядро
, и пусть ядро  непрерывно по совокупности переменных при
непрерывно по совокупности переменных при
 (7)
(7)
а свободный член  непрерывен на
непрерывен на  .
.
Тогда справедливы следующие два утверждения:
а) Если решение  изолировано и ненулевого индекса (в пространстве C), то при достаточно больших n система уравнений (5) разрешима и
изолировано и ненулевого индекса (в пространстве C), то при достаточно больших n система уравнений (5) разрешима и
 (8)
(8)
б) Если ядро  имеет частную производную по x, непрерывную по совокупности переменных в области (7), и если линейное однородное интегральное уравнение
имеет частную производную по x, непрерывную по совокупности переменных в области (7), и если линейное однородное интегральное уравнение

имеет лишь нулевое решение, то решение системы (5) при достаточно больших n существует и единственно, имеет место сходимость (8) и справедлива двусторонняя оценка
 (9)
(9)
где 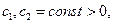
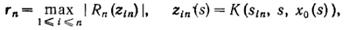
 - остаточный член квадратурной формулы (6).
- остаточный член квадратурной формулы (6).
Доказательство. Пространства E и 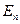 и проектор
и проектор  построим так же, как при доказательстве аналогичной теоремы для линейных интегральных уравнений (лекция 10, теорема 2). Уравнение (4) будем рассматривать как операторное уравнение
построим так же, как при доказательстве аналогичной теоремы для линейных интегральных уравнений (лекция 10, теорема 2). Уравнение (4) будем рассматривать как операторное уравнение  . Непрерывность ядра
. Непрерывность ядра  в области (7) влечет за собой полную непрерывность оператора
в области (7) влечет за собой полную непрерывность оператора
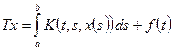
на шаре  как оператора из E в пространство C, а значит, и как оператора в E. В лекции 10 показано, что проекторы
как оператора из E в пространство C, а значит, и как оператора в E. В лекции 10 показано, что проекторы  как оператора из C в пространство E сильно стремятся к оператору вложения C в E. Отсюда следует (утверждение 7), что в рассматриваемом случае выполнено условие (1).
как оператора из C в пространство E сильно стремятся к оператору вложения C в E. Отсюда следует (утверждение 7), что в рассматриваемом случае выполнено условие (1).
|
|
|
Система уравнений (5) равносильна уравнению  , в котором оператор
, в котором оператор  определен на элементах
определен на элементах  из множества
из множества  формулой
формулой
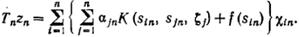
Приведем разность  к виду
к виду

откуда, используя из лекции 10 (*), лемму 1 и
 ,
,
а также равномерную непрерывность и ограниченность  в замкнутой области (7), получим соотношение (2).
в замкнутой области (7), получим соотношение (2).
В силу утверждения 3 индекс решения  уравнения (4) одинаков в пространствах C и E; по предположению он отличен от нуля. Утверждение (а) теоремы следует из теоремы 2. Заметим, что решение
уравнения (4) одинаков в пространствах C и E; по предположению он отличен от нуля. Утверждение (а) теоремы следует из теоремы 2. Заметим, что решение 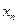 уравнения
уравнения  и решение
и решение  системы (5) связаны соотношением
системы (5) связаны соотношением  , и что
, и что
 (10)
(10)
Перейдем к утверждению (б). Существование непрерывной в области (7) частной производной  влечет непрерывную дифференцируемость T в
влечет непрерывную дифференцируемость T в  как оператора из E в C, а тем более как оператора в E. Так как операторы
как оператора из E в C, а тем более как оператора в E. Так как операторы  сильно сходятся к оператору вложения C в E, то отсюда следует, что соблюдаются условия (8), (9) теоремы 1 (лекция 8). Поскольку оператор
сильно сходятся к оператору вложения C в E, то отсюда следует, что соблюдаются условия (8), (9) теоремы 1 (лекция 8). Поскольку оператор

вполне непрерывен в E и уравнение  имеет по условию лишь нулевое решение, то оператор
имеет по условию лишь нулевое решение, то оператор  непрерывно обратим.
непрерывно обратим.
Операторы  и
и  непрерывно дифференцируемы в
непрерывно дифференцируемы в  , причем для любых
, причем для любых  и
и  имеем
имеем
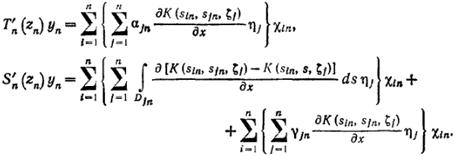
Пользуясь равномерной непрерывностью и ограниченностью  в замкнутой области (7), можно показать, что выполняются условия (10), (11) теоремы 1 (лекция 8). Теперь утверждение (б) следует из этой теоремы. В частности, оценка (9) вытекает из (13) теоремы 1 и соотношения (10); заметим, что
в замкнутой области (7), можно показать, что выполняются условия (10), (11) теоремы 1 (лекция 8). Теперь утверждение (б) следует из этой теоремы. В частности, оценка (9) вытекает из (13) теоремы 1 и соотношения (10); заметим, что  .
.
Теорема доказана.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 572; Нарушение авторских прав?; Мы поможем в написании вашей работы!