Модификации метода Эйлера

Разовьем последний из подходов к построению метода Эйлера. Очевидно, применение к интегральному равенству (4) других простейших квадратурных формул будет порождать новые методы численного интегрирования задачи Коши (1)-(2).

Так, если в (4) использовать простейшую квадратурную формулу правых прямоугольников (5.7), придем к методу

y_i+1 = y_i + hf(x_i+1, y_i+1), i = 0, 1, …, n. (6)

Этот метод называют неявным (или обратным) методом Эйлера, поскольку для вычисления неизвестного значения y_i+1» y(x_i+1) по известному значению y_i» y(x_i) требуется решать уравнение, в общем случае нелинейное. Имеет ли свою сферу применения подобный метод, порядок которого такой же, как и у явного метода Эйлера (14.8) (первый), и один шаг вычислений по которому столь трудоемок? Положительный ответ на этот вопрос будет дан далее.

Применение к интегралу в (4) простейшей квадратурной формулы трапеций приводит тоже к неявному методу

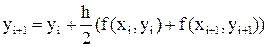, i = 0, 1,..., n, (7)

который будем называть методом трапеций. Квадратурная формула трапеций, как известно, на порядок точнее формул левых и правых прямоугольников. Отсюда вытекает более высокий (на единицу) порядок точности метода трапеций (7) по сравнению с явным и с неявным методами Эйлера (5) и (6), т. е. метод трапеций (7) — это метод второго порядка.

Некоторый интерес представляет совместное применение явного метода Эйлера и неявного метода трапеций.

По форме равенство (7) представляет собой скалярную задачу о неподвижной точке относительно неизвестного значения y_i+1. Поэтому, если в правую часть (7) подставить хорошее начальное приближение 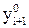, подсчитываемое по формуле (5), то тогда само это равенство можно считать шагом метода простых итераций для уточнения этого значения. Таким образом, получаем гибридный метод

, i = 0, 1, …, n, (8)

который называют методом Хойна.

Ясно, что можно достичь большей точности, если, исходя из того же начального приближения

,

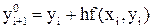сделать не одну, а несколько итераций по методу трапеций:

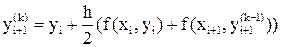, i = 1, 2,..., n. (9)

Такой вариант совместного применения метода Эйлера и метода трапеций называют усовершенствованным методом Эйлера-Коши с итерационной обработкой. Делать много итераций по формуле (9) не рекомендуется (обычно их выполняют не более трех-четырех). Совпадение определенного числа разрядов в полученных числах 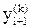и 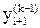говорит о точности, с которой решено методом простых итераций уравнение (7) относительно y_i+1, а вовсе не о том, что с такой точностью найдено значение y(x_i+1).

Чтобы получить следующую модификацию метода Эйлера, проинтегрируем уравнение (1) по отрезку [x_i–1; x_i+1]. Имеем

,

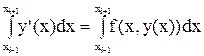откуда следует равенство

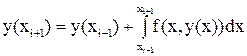. (10)

Применяя к последнему интегралу одноточечную квадратурную формулу средних прямоугольников (12.10) и заменяя значения y(x_i–1) и y(x_i) известными приближенными значениями y_i–1 и y_i соответственно, из (10) выводим формулу для подсчета приближенного значения у(x_i+1)

y_i+1 = y_i–1 + 2hf(x_i, y_i), i = 1, 2,..., n – 1, (11)

которую будем называть уточненным методом Эйлера.

Как известно, квадратурная формула прямоугольников (средней точки) имеет тот же порядок точности, что и квадратурная формула трапеций, так что уточненный метод Эйлера (11) тоже является методом второго порядка.

Дата добавления: 2014-01-07