Введение векторных и скалярных потенциалов в случае монохроматических электромагнитных полей

1. Определение с помощью потенциалов монохроматических полей возбуждаемых сторонними электрическими токами.

Для анализа монохроматических полей необходимо от полученных представлений (3.12), (3.5), (3.14) перейти к соответствующим представлениям для комплексных амплитуд A ^e (r,ω), H ^e (r,ω), E ^e (r,ω). При этом операторы дифференцирования и интегрирования по времени соответственно заменяются на

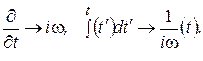
С учетом этого соотношения (3.13), (3.7), (3.15) приводятся к виду

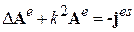, (3.16)

Н ^e = rot A ^e, (3.17)

. (3.18)

Здесь (3.16) – УГ для векторного электрического потенциала.

Соотношения (3.16)-(3.18) сохраняют смысл при переходе к средам с проводимостью, для этого достаточно заменить в них 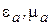на

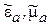, при этом . Отметим также, что связь электрического поля с потенциалами и условие калибровки Лоренца в случае гармонических полей принимают вид

(3.19)

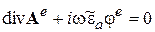. (3.20)

2. Определение с помощью потенциалов гармонических полей возбуждаемых сторонними магнитными токами.

Аналогично можно рассмотреть УМ со сторонним магнитным током, которые определяют поля E ^m, H ^m

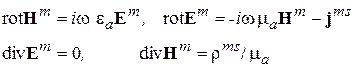(3.21)

В случае возбуждения полей магнитным сторонним током определим связь электрического поля с векторным магнитным потенциалом соотношением

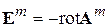. (3.22)

Далее воспользуемся принципом перестановочной двойственности, дополнив его соотношением

,

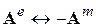вытекающим из сопоставления (3.17) и (3.22).

В результате из (3.18) получим, что поле Н ^m, создаваемое сторонним магнитным током, определяются через векторный магнитный потенциал А ^m как

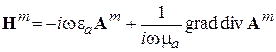. (3.23)

а из (3.16), что векторный магнитный потенциал А ^m удовлетворяет УГ

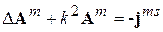. (3.24)

3) Определение с помощью векторных потенциалов электромагнитного поля, возбуждаемого суперпозицией сторонних электрических и магнитных токов.

Полное электромагнитное поле, возбуждаемое суперпозицией электрических и магнитных сторонних токов, определяется суперпозицией полей

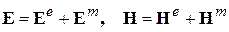. (3.25)

где в соответствии с (3.17), (3.18), (3.22), (3.23)

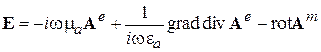, (3.26)

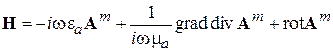, (3.27)

а векторные потенциалы А ^e и А ^m удовлетворяют уравнениям (3.16) и (3.24).

Таким образом, мы получили выражения для электрических и магнитных полей через векторные потенциалы.

Ещё раз подчеркнем, что анализ и решение уравнений для А ^e и А ^m существенно упрощаются благодаря тому, что правые части (3.16) и (3.24) – это сторонние токи j ^e и j ^m. В частности, из уравнений видно, что в декартовой системе координат вектор А ^e (А ^m), удовлетворяющий неоднородному УГ, параллелен создающему его стороннему току. Действительно, разложим векторы A и j по единичным ортамвдекартовой системе координат e _i, i=x,y,z: A = A_x e _x + A_y e _y + A_z e _z, j = j_x e _x + j_y e _y + j_z e _z. Тогда УГ для вектора A в декартовой системе координат распадается на 3 независимых скалярных УГ

D A_i + k²A_i = - j_i, i=x,y,z, (3.28)

то - есть x -овая (y -овая, z -овая) компоненты потенциала определяются соответствующими компонентами стороннего тока. Если мы ищем, например, поле излучения тока, направленного вдоль оси z декартовой системы координат, то j_x=j_y =0 и решения однородных УГ для A_x и A_y мы вправе положить равными нулю. Таким образом, задача анализа поля излучения тока j_z сводится к решению скалярного УГ

D A_z+k²A_z = - j_z. (3.29)

Это очень полезное свойство векторных потенциалов будет использовано ниже при анализе излучения элементарных источников (диполей).

Таким образом, после долгих преобразований мы добрались до уравнений, удобных для решения.

Нужно сделать еще несколько замечаний.

Замечание 1.

В УМ (3.1) не были учтены токи проводимости. С введением потенциалов для УМ при учете токов проводимости можно ознакомиться по [1], п.1.9.

Замечание 2. О других калибровках и калибровочной инвариантности

В выборе связи между div А ^э и j^э имеется произвол. Обсудим этот вопрос на примере гармонических полей.

Соотношениям (3.17) и (3.18) при калибровке (3.20) удовлетворяет бесконечное множество векторных и скалярных потенциалов. Действительно, введем вместо векторного потенциала А ^e потенциал

А' ^e= А ^e + grad y, (3.30)

где y - некоторое скалярное поле. Магнитное поле, как следует из (3.17), при такой замене остается неизменным. Далее аналогично (3.19) можно положить

,

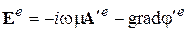где j¢ ^e - новый скалярный потенциал. Для того, чтобы электрическое поле осталось при такой замене неизменным, должна выполняться следующая связь между j ^e и j¢ ^e

j^э = j'^э + i wm _a y. (3.31)

Далее аналогично предыдущему получим, что векторный потенциал А' ^e удовлетворяет уравнению вида (3.16), если А' ^e и j¢ ^e удовлетворяют условию калибровки

. (3.32)

Подставляя в (3.32) соотношения (3.31) и (3.30) и учитывая условие (3.20), получим, что скалярный потенциал y должен удовлетворять однородному скалярному УГ

Dy+ k ²y=0. (3.33)

Таким образом, используя различные частные решения (3.33), можно построить бесконечное множество векторных и скалярных электрических потенциалов, оставляющих неизменными электрическое и магнитное поля.

Свойство неизменности значений электрического и магнитного полей при введении различных векторных (А ^e) и скалярных (j ^e) потенциалов называется калибровочной инвариантностью.

Помимо условия Лоренца возможно наложение других условий на выбор связи. Например, в теории поля используется так называемая кулоновская калибровка, при которой требуют выполнение условия div А ^e = 0.

3 замечание.

Векторное УГ для потенциала A распадается на три независимых уравнения для

компонент A_i, i=x,y,z, только в декартовой системе координат. В других ортогональных криволинейных системах координат для перехода от векторного УГ к скалярным уравнениям необходимо использовать представление (3.2), при этом в общем случае получают три взаимосвязанных скалярных уравнения. Так, в цилиндрической системе координат (r, φ, z) компоненты А_r и А _φ удовлетворяют системе двух связанных уравнений, а компонента А_z – уравнению (3.29). В сферической системе координат (R, θ, φ) все компоненты А_R, А _θ, А _φ удовлетворяют системе из трех связанных уравнений (см. задачи на стр. 41-43 в [1]).

4 замечание. Вы можете меня спросить, а какому уравнению удовлетворяет скалярный потенциал j ^e (j ^m) и нельзя ли вместо решения уравнения для векторного потенциала А ^e (А ^m) решать совместно уравнения для А ^e и j ^e (А ^m и j ^m)?

Уравнения для скалярного потенциала легко получить. Покажем на примере j ^e. Воспользуемся 3-м УМ (3.1), перейдем к комплексным амплитудам и подставим в (3.1) представление Е ^e из (3.19). Получим

divgrad j ^e + i wm _a div А ^e = - r ^es ¤e _а.

Воспользовавшись условием калибровки (3.20), исключим div А ^э. Получим

Dj ^e + k² j ^e = - r ^es ¤e _а. (3.34)

В (3.34) учтено, что div grad = D. Таким образом, скалярный электрический потенциал удовлетворяет неоднородному скалярному УГ.

Можно решить вначале неоднородное уравнение для скалярного потенциала (3.34), затем подставитьj ^e в неоднородное УГ для А ^e, которое можно получить для гармонических полей из (3.11). Тогда уравнение (3.11) примет вид (3.16)

,

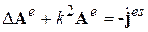Решив последнее уравнение, находим по известным j ^e и А ^e значения полей Е ^e и Н ^e. Окончательный результат совпадает с вычислением Е ^e и Н ^e только через векторный потенциал А ^e.

5-е замечание касается вихревого и потенциального характера полей.

Как было сказано в начале лекции, в стационарном случае поле Н является чисто вихревым, а поле Е – в статике – чисто потенциальным. Зададим вопрос: что представляет собой переменное электромагнитное поле, удовлетворяющее УМ? Может ли оно быть представлено в виде суммы вихревого и потенциального полей?

Вопрос очень не простой.

Рассмотрим УМ со сторонними электрическими токами и зарядами (3.1). Казалось бы, из вида УМ (3.1) можно сделать следующий вывод: магнитное поле Н – вихревое, т.к. div Н = 0, а электрическое поле E – потенциально, т.к. div E ¹ 0. Однако это утверждение по отношению к электрическому полю неверно. Строго представить поля E и Н как суперпозицию вихревого поля Н и потенциального поля E нельзя. Это видно из представлений (3.15), (3.18) электрического поля через векторный А ^e и скалярный j ^e потенциалы: электрическое поле содержит как вихревую, так и потенциальную составляющую. Таким образом, можно предположить, что поле Н – вихревое, а поле E – суперпозиция вихревого и потенциального полей. Если бы последнее утверждение относительно E было верно, то согласно теореме Гельмгольца отыскание поля E можно было бы свести к решению независимых векторного и скалярного уравнений Пуассона для некоторых потенциалов А и j. Однако это не так. А и j удовлетворяют не уравнениям Пуассона, а уравнениям Гельмгольца. Остается предположить, что переменное электромагнитное поле представляет собой более сложный объект, не представимый суперпозицией вихревого и потенциального полей, а «сочетающий признаки вихревого и потенциального полей».

В дальнейшем понимание этого утверждения мы углубим, анализируя структуру электромагнитное поля простейшей антенны – электрического диполя – в различные моменты времени.

6-е замечание. Мы можем определять физическое поле либо через электрическое (E) и магнитное (Н) поля, либо через векторный (А) и скалярный (j) потенциалы (для определенности все рассуждения ведем относительно полей, создаваемых электрическими зарядами и токами). Что физичнее или фундаментальнее: пара E, Н или А, j? Вопрос нетривиальный и ответ на него многоплановый.

С позиций физического наблюдения существенно, что на макроуровне измеряют поля E и Н. Так что можно утверждать, что на макроуровне физический смысл имеют именно E и Н. С другой стороны, если бы между E и Н, с одной стороны, и А и j, с другой, имелось взаимно однозначное соответствие, с таким же основанием мы могли бы говорить об измерении А и j. Однако мы знаем, что потенциалы А и j вводятся неоднозначным образом. Неоднозначность введения А и j и независимость от этой неоднозначности полей E и Н часто рассматривают как аргумент в пользу того, что А и j – вспомогательные величины, не имеющие прямого физического смысла.

Тем не менее есть основания утверждать, что на микроуровне векторный потенциал является более фундаментальной величиной, чем E и Н. Этот вопрос обсуждается в курсе Фейнмановских лекций по физике [2], т.6, гл.15. В 1956-м году американские физики Ааронов и Бом предложили поставить эксперимент, указывающий на прямое физическое доказательство фундаментальной роли векторного потенциала.

Экран

Соленоид

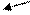
Металлическая пластина

Щели

Электрон

Рис.3.1

Известен эксперимент по дифракции электронов на двух щелях, когда на экране наблюдается интерференционная картина. Интерпретацию этого эксперимента в классической теории дать нельзя, его объясняет только квантовая механика. Ааронов и Бом предложили модифицировать этот эксперимент следующим образом: поставить в тени за щелями бесконечный соленоид (рис. 3.1). Известно, что внутри соленоида магнитная индукция В ¹ 0, а вне соленоида В = 0. Однако векторный потенциал вне соленоида не равен нулю, т.к. из условия В = rot A = 0 еще не следует А = 0. Если результат интерференции при дифракции электронов на щелях будет зависеть от того, включено магнитное поле в соленоиде или нет, это будет означать влияние векторного потенциала А на дифракцию. Были проведены эксперименты в предложенной постановке и предположение Ааронова и Бома о влиянии векторного потенциала А на дифракцию электронов подтвердилось (см. [2]). Это означает, что поле А действительно реально и, более того, действует на электроны там, где электромагнитное поле равно нулю. Таким образом, на квантовом уровне векторный потенциал является фундаментальной величиной, а не электромагнитное поле.

Литература к лекции 3.

Метод векторных потенциалов изложен по кн.

1. Марков Г.Т., Петров Б.М., Грудинская Г.П. Электродинамика и распространение радиоволн. М. 1979. (стр. 35-40)

Обсуждение фундаментальной роли векторного потенциала см. в

2. Фейнман Р., Лейтон Р., Сэндс М.. Фейнмановские лекции по физике, т. 6, Электродинамика. -М.: МИР, 1966, (стр. 17-26).

Дата добавления: 2014-01-07