Анализ на чувствительность оптимального решения к изменению коэффициентов целевой функции

Лекция 7

Тема: “ Анализ на чувствительность”

Поставим цель: найти интервалы изменения коэффициентов целевой функции, при которых оптимальные значения управляющих переменных остаются неизменными.

Заметим, что уравнение целевой функции никогда не используется в качестве ведущего уравнения. Поэтому любые изменения коэффициентов целевой функции окажут влияние только на f -уравнение результирующей симплекс-таблицы.

Пример 1. Фирма изготавливает два вида красок для внутренних (В) и наружных (Н) работ. Используется два расходных продукта А и С, суточные запасы которых ограничены (не более 6 т для продукта А и не более 8 т для С). Расходы продуктов А и С на 1 т красок приведены в таблице:

	Н	В
А
С

Суточный спрос на В не превышает спроса на Н более чем на 1 т. Спрос на краску В не превышает 2 т. Оптовые цены: 3 тыс. $ за 1 т краски Н и 2 тыс. $ за 1 т краски В.

Какое количество краски каждого вида должна производить фабрика, чтобы доход от продажи был максимальным? В каких пределах может изменяться цена на товар, так чтобы не изменялся оптимальный план?

Рассмотрим следующую задачу линейного программирования:

Приведём задачу к каноническому виду и составим симплекс-таблицу:

Базис
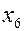
	2
	-1
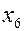
f	-3	-2
Базис
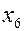
		3/2		-1/2
		1/2		1/2
		3/2		1/2
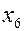
f		-1/2		3/2
Базис
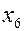
			2/3	-1/3			4/3
			-1/3	2/3			10/3
			-1
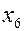
			-2/3	1/3			2/3
f			1/3	4/3			38/3

Предположим, что в рассматриваемой задаче цены на краску Н и В равны тыс. долл. для краски Н и тыс. долл. на краску В вместо 3 и 2 тыс. долларов соответственно, где и может быть как положительным, так и отрицательными числами. Целевая функция в этом случае имеет следующий вид: .

Если воспользоваться данными начальной таблицы и выполнить все вычисления, необходимые для получения оптимальной симплекс-таблицы, то последнее f -уравнение будет выглядеть следующим образом:

f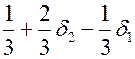

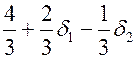
Условие оптимальности запишется следующим образом:

,

.

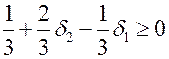Комментарий. С самого начала функция прибыли имела вид . Изменение цен дает добавку к прибыли . Поскольку для оптимального плана значения переменных и известны, получаем, что появление добавок и приводит к изменению функции f на величину .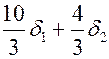

Теперь определим, с какими коэффициентами и войдут в остальные позиции f -строки. Следует понять, как изменились теневые цены свободных переменных (или, что все равно, дефицитных ресурсов) и . Для этого подставим в функцию выражение через свободные переменные, которое мы получили в последней симплекс таблице, то есть

, ,

откуда

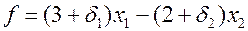Û

.

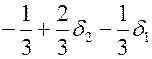Следовательно, коэффициенты при переменных и равны и 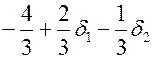соответственно. То есть коэффициенты при и равны коэффициентам при соответствующих переменных в -строке и -строке, полученной ранее таблицы.

Базис
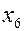
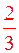
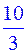
			-1
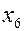
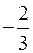
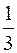
f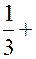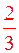

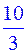
2. Специальные задачи линейного программирования. Математическая постановка транспортной задачи. Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления 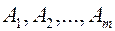в n пунктов назначения . При этом в качестве критерия оптимальности обычно берётся либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки.

Рассмотрим транспортную задачу в качестве критерия оптимальности, которой взята минимальная стоимость перевозок всего груза. Обозначим через 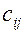тарифы перевозки единицы груза из i -ого пункта отправления в j -ый пункт назначения, через 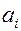- запасы груза в i -ом пункте отправления, через 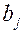- потребности в грузе в j -ом пункте назначения, через 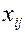- количество единиц груза, перевозимого из i -ого пункта отправления в j -ый пункт назначения. Тогда математическая постановка задачи состоит в определении минимального значения функции

(1)

при условиях

(2)

Поскольку переменные 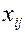удовлетворяют условиям (2), обеспечиваются доставка необходимого количества груза в каждый из пунктов назначения, вывоз имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки.

Определение 1. Всякое неотрицательное решение систем линейных уравнений (2), определяемое матрицей 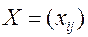, называется планом транспортной задачи.

Определение 2. План , при котором функция (1) принимает минимальное значение, называется оптимальным планом транспортной задачи.

Обычно исходные данные транспортной задачи записывают в виде таблицы.

Пункты отправления	Пункты назначения	Запасы
	…		…
		…		…
…	…	…	…	…	…	…
		…		…
…	…	…	…	…	…	…
		…		…
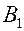
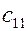
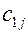
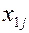
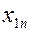
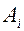
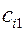
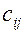
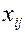
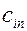
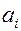
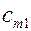
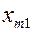
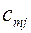
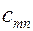
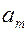
Потребности		…		…		...

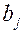
Очевидно, общее наличие груза у поставщиков равно , а общая потребность в грузе в пунктах назначения равна 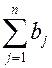единиц.

Определение 3. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т.е.

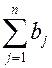=, (3)

то модель такой транспортной задачи называется закрытой. Если же указанное условие не выполняется, то модель транспортной задачи называется открытой.

Теорема. Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т.е. чтобы выполнялось равенство (3).

В случае превышения запаса над потребностью, т.е. >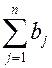, вводится фиктивный (n +1)-й пункт назначения с потребностью = -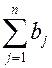и соответствующие тарифы считаются равными нулю: Полученная задача является закрытой транспортной задачей.

Аналогично, при <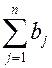вводится фиктивный (m +1)-й пункт отправления с запасом груза 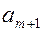=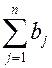-и тарифы полагаются равными нулю: В дальнейшем будем рассматривать закрытую модель транспортной задачи.

Дата добавления: 2014-01-07