Элементы комбинаторики. Классическое определение вероятности

Классическое определение вероятности

При моделировании социально-правовых явлений, прогнозировании и принятии решений в юридической практике часто бывает необходимо численно оценить возможность наступления того или иного события. Очевидно, что разные события обладают разной степенью возможности их наступления. Например, очевидно, что возможность раскрытия уголовного дела группой следователей и возможность раскрытия этого же дела одним следователем различны. Но для гарантированного успеха необходимо знать, насколько они отличаются. Поэтому для сравнения событий надо ввести численную меру возможности их наступления.

Численная мера возможности наступления случайного события называется вероятностью этого события.

Впервые понятие вероятности было введено в XVII веке для анализа азартных игр.

Теперь рассмотрим, как можно вычислить вероятность некоторых случайных событий. Начнем с классического метода вычисления вероятности. Оно основано на предположении о равновозможности событий, составляющих полную группу. Равновозможность таких событий исходит из их симметричности в испытании и не определяется формальным образом, а лишь поясняется на примерах. Равновозможными событиями, образующими полную группу, являются выпадение любой грани геометрически правильного куба, изготовленного из однородного материала (игрального кубика); вытаскивание карты из колоды и т.д.

Итак, пусть исходы некоторого испытания, образующие полную группу событий, равновозможны и число их конечно. Такие исходы называются элементарными исходами (элементарными событиями). При этом говорят, что испытание сводится к схеме случаев. Зачастую, наибольший интерес представляет наступление не элементарного события, а некоторого случайного события, которое включает в себя несколько элементарных. Например, при вытаскивании карты из колоды нас может интересовать появление туза любой масти, т.е. одной из четырех карт. Элементарные исходы, в которых интересующее нас событие наступает, называются благоприятствующими этому событию.

Классическое определение вероятности.

Вероятность случайного события A равна отношению числа исходов, благоприятствующих этому событию, к общему числу элементарных исходов.

Вероятность случайного события A обозначается P(A).

P(A) = , (5.1)

где m - число элементарных исходов благоприятствующих событию A,

n - общее число элементарных исходов.

Пример 5.1. Какова вероятность того, что случайно вытащенная карта из колоды окажется тузом?

Решение. В данном испытании количество элементарных исходов n= 36 (возможность вытащить любую карту из колоды одинакова и все эти события образуют полную группу). Число благоприятных исходов соответствует числу тузов m= 4. Следовательно, вероятность вытащить туза

P(A) = m/n = 4/36 = 1/9.

Пример 5.2. Найти вероятность выпадения числа очков большего 4 при бросании игрального кубика.

Решение. При бросании кубика события, составляющие в выпадении числа очков 1, 2, 3, 4, 5 и 6, являются элементарными исходами, т.к. они равновозможны и образуют полную группу. Число благоприятствующих событий 2 - выпадение 5 или 6 очков. Значит, вероятность того, что выпадает число больше 4:

P(A) = 2/6 = 1/3.

Необходимо заметить, что формула (5.1) не является точным определением вероятности событий, а лишь служит для вычисления вероятности событий в тех испытаниях, которые обладают симметрией возможных конечных исходов, т.е., как говорят, сводятся к схеме случаев.

Рассмотрим свойства вероятности случайных событий.

1. Вероятность любого события больше либо равна нулю и меньше либо равна единице:

.

Действительно, количество элементарных исходов m, благоприятствующих случайному событию, не может быть больше общего числа элементарных исходов n, т.е. всегда 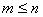. С другой стороны, m – неотрицательное число, т.е. 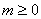. Таким образом, мы имеем следующее неравенство 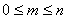. Поделив его на n, получим или 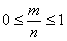, что по определению вероятности и дает .

2. Вероятность достоверного события равна единице.

P(D)= 1, где D – достоверное событие.

Если событие достоверное, то оно должно наступать при любом исходе испытания. Значит, все элементарные исходы испытания являются благоприятствующими, т.е. m=n. И, следовательно, вероятность достоверного события .

3. Вероятность невозможного события равна нулю.

P(N)=0, где N – невозможное событие.

Если событие является невозможным, то оно не должно наступать ни при одном исходе испытания. Значит, ни один исход не является благоприятствующим, т.е. m=0. И вероятность невозможного события .

Для вычисления вероятностей различных случайных событий мы должны научиться подсчитывать количество элементарных и благоприятных исходов для этих событий. Во многих практических задачах для этого необходимо воспользоваться формулами комбинаторики.

Во всех вышеперечисленных испытаниях мы рассматривали появление одного объекта из некоторого конечного множества. При этом число исходов испытания находилось достаточно просто. Однако, чаще всего, при вычислении вероятности какого-либо события необходимо уметь находить число комбинаций выбора нескольких объектов.

Область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов, называется комбинаторикой. В комбинаторных задачах необходимо подсчитать, сколькими способами можно сделать тот или иной выбор, выполнить то или иное требование, выполнить какое-либо условие.

Первые комбинаторные задачи были связаны с азартными играми: картами, костями, «орлянкой». Наиболее любопытные игроки интересовались, например, тем, сколькими способами можно выбросить данное количество очков, бросая две или три кости или сколькими способами можно получить двух тузов при раздаче карт. Основы теоретических положений комбинаторики были разработаны французскими учеными Блезом Паскалем и Пьером Ферма в XVII веке.

Дальнейшее развитие комбинаторика получила в работах Я. Бернулли, Г. Лейбница и Л. Эйлера.

В наше время комбинаторика получила новый толчок для развития в связи с появлением быстродействующих ЭВМ и широким использованием методов дискретной математики. Комбинаторные методы используются для решения транспортных задач, задач по составлению расписаний, для разработки, кодирования и декодирования шифров, в задачах линейного программирования, статистики, теории информации.

Большинство комбинаторных задач может быть решено с помощью двух основных правил: правила суммы и правила произведения.

Дата добавления: 2014-01-07