Деревья решений

Критерий наиболее вероятного исхода.

Этот критерий основан на преобразовании случайной ситуации в детерминированную путем замены случайной величины единственным значением, имеющим наибольшую вероятность реализации.

Предположим, что доход от изделия j равен c_j и p_j – дискретная плотность распределения с_j. Пусть c_j* выбрано так, что p_j (c_j*)=max p_j(c_j) для всех c_j. Тогда c_j* можно рассматривать как детерминированное значение дохода от изделия j.

Этот критерий можно считать упрощением более сложного правила принятия решения в условиях риска. Такое упрощение проводится исходя из того, что с практической точки зрения знание наиболее вероятного исхода обеспечивает необходимую информацию для принятия решения. Например, всегда существует положительная (хотя и очень малая) вероятность того, что самолет может потерпеть аварию, но несмотря на это, большинство пассажиров предполагают, что полет пройдет успешно.

Когда нельзя применять критерий наиболее вероятного исхода.

1. Когда рассматриваемая случайная величина принимает большое число значений, каждое из которых имеет небольшую вероятность реализации (меньше 0,05).
2. Когда несколько значений случайной величины имеют равные вероятности реализации.

Нами были рассмотрены критерии, позволяющие делать выбор из совокупности “одноэтапных” альтернатив. При этом подразумевалось, что решения, принимаемые в будущем, не зависят от решений, принимаемых в текущий момент.

Теперь рассмотрим “многоэтапный” процесс принятия решений, в котором взаимозависимые решения принимаются последовательно. Графически такие процессы могут быть представлены с помощью дерева решений.

Пример. Фирма должна принять решение о строительстве крупного или небольшого предприятия. Небольшое предприятие впоследствии можно расширить. Решение определяется будущим спросом на продукцию, которую предполагается выпускать. Строительство крупного предприятия экономически оправдано при высоком уровне спроса. С другой стороны, можно построить небольшое предприятие и через два года принять решение о его расширении.

Поставленная задача является многоэтапной, так как если фирма решит строить небольшое предприятие, то через два года она должна будет принять решение о его расширении.

Процесс принятия решения состоит из двух этапов:

• решение в настоящий момент о размере предприятия,
• решение, принимаемое через два года, относительно его расширения, если на первом этапе принято решение о строительстве небольшого предприятия.

Данную задачу представим в виде дерева решений.

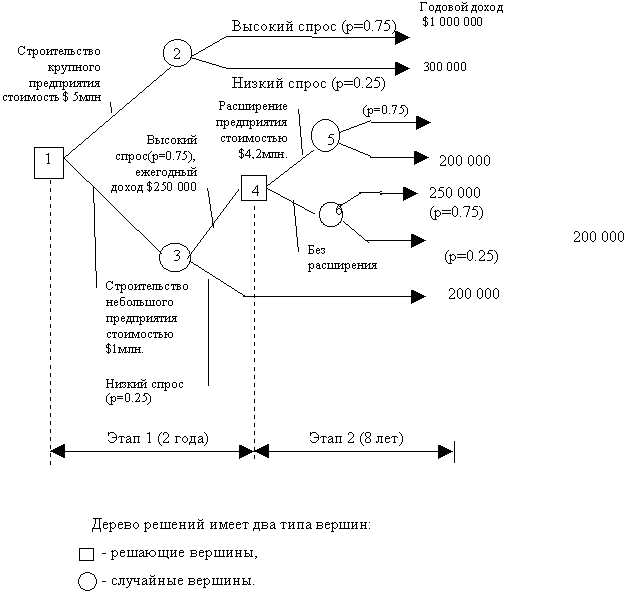
Начиная с вершины 1 (решающей), необходимо принять решение относительно размера предприятия.

Вершина 2 является случайной, из нее выходя две ветви, соответствующие низкому и высокому уровням спроса в зависимости от сложившейся ситуации на рынке. Каждая из этих ситуаций представлена соответствующим значением вероятности ее реализации.

Вершина 3 также является случайной, из нее выходят две ветви, соответствующие разным уровням спроса.

Фирма будет рассматривать возможность расширения небольшого предприятия только в том случае, если спрос по истечении двух первых лет установился на высоком уровне.

В вершине 4 принимается решение, из нее выходя две ветви, соответствующие решениям: расширять или не расширять.

Вершины 5 и 6 будут случайными с двумя выходящими ветвями из каждой, соответствующими двум уровням спроса.

Данные для поиска решения должны включать:

1. вероятности реализации каждой ветви, выходящей из случайной вершины;
2. доходы (или расходы), связанные с каждой альтернативой решения задачи.

Предположим, что фирма рассматривает задачу на 10 период. Анализ рыночной ситуации показывает, что вероятности высокого и низкого спроса равны соответственно 0.75 и 0.25. Строительство крупного предприятия обойдется фирме в 5 млн. долларов, а небольшого – 1 млн. долларов. Затраты на расширение через два года небольшого предприятия оцениваются в 4,2 млн. долларов.

Ежегодные доходы для каждой из возможных альтернатив.

1. Крупное предприятие при высоком (низком) спросе дает 1 млн. долларов (300 000 долл.) ежегодно.
2. Небольшое предприятие при низком спросе дает 200 000 долларов ежегодно.
3. Небольшое предприятие при высоком спросе дает 250 000 долларов ежегодно в течение 10 лет.
4. Расширенное предприятие при высоком (низком) спросе дает 900 000 (200 000) долларов ежегодно.
5. Небольшое предприятие без расширения при высоком уровне спроса в течение первых двух лет и последующем низком спросе дает 200 000 долларов в год за остальные 8 лет.

Оценим результаты для каждой из альтернатив, для этого воспользуемся критерием ожидаемого значения. Окончательный результат должен показать, какие решения необходимо выбирать в вершинах 1 и 4.

Начнем вычисления с этапа 2, а затем перейдем к этапу 1. Для последних 8 лет альтернативы, относящиеся к вершине 4, оцениваются следующим образом:

М{чистая прибыль | расширение}=(900000* 0.75+ 200000* 0.25 * 8- 420000 = 1600000 долл.

М{чистая прибыль | без расширения}= (250000* 0.75+200000*0.25)*8 = 1 900 000 долл.

Таким образом, в вершине 4 выгоднее не проводить расширения предприятия. Теперь оставляем одну ветвь, выходящую из вершины 4, которой соответствует чистая прибыль в 1 900 000 долларов за остальные восемь лет.

Перейдем к вычислениям на этапе 1 для вершины 1.

М{чистая прибыль | крупное предприятие}= (1 000 000*0.75 + 300 000*0.25)*10 -

5 000 000 = 3 250 000 долл.

М{чистая прибыль | небольшое предприятие}= (1 900 000 + 500 000*0.75 +

2 000 000*0.25 - 1 000 000 = 1 300 000 долл.

Таким образом, оптимальное решение в вершине 1 является решение о строительстве крупного предприятия. Это решение исключает необходимость рассмотрения альтернатив в вершине 4.

Дата добавления: 2014-01-07