Свободные гармонические колебания и их характеристики

Лекция № 7

Механические колебания

5.1. Свободные гармонические колебания и их характеристики.

5.2. Сложение одинаково направленных и взаимно перпендикулярных гармонических колебаний.

5.3. Дифференциальное уравнение гармонических колебаний и его решение.

5.4. Энергия гармонических колебаний.

5.5. Пружинный, математический и физический маятники.

Колебания − это движения или процессы, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебания, повторяются через равные промежутки времени. Наиболее важными характеристиками колебания являются: смещение, амплитуда, период, частота, циклическая частота, фаза.

Простейший вид периодических колебаний − это гармонические колебания. Гармонические колебания − это периодическое изменение во времени физической величины, происходящее по закону косинуса или синуса. Уравнение гармонических колебаний имеет вид

x = A cos(w t + j₀) или x = A sin(w t + j₁), (5.1.1)

где .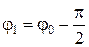

1) Смещение x − это величина, характеризующая колебания и равная отклонению тела от положения равновесия в данный момент времени.

2) Амплитуда колебаний А − это величина, равная максимальному отклонению тела от положения равновесия.

3) Период колебаний T − это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Единица измерения [ T ] = 1 с.

За период система совершает одно полное колебание.

4) Частота колебаний n − это величина, равная числу колебаний, совершаемых в единицу времени (за 1 секунду). Единица измерения [n]= 1 Гц. Частота определяется по формуле

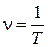. (5.1.2)

5) Циклическая частота w − это величина, равная числу полных колебаний, совершающихся за 2p секунд. За единицу циклической частоты принята угловая частота, при которой за время 1 с совершается 2p циклов колебаний, [w]= с⁻¹. Циклическая частота связана с периодом и частотой колебаний соотношением

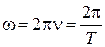. (5.1.3)

6) Фаза колебаний w t + j₀ − фаза указывает местоположение колеблющейся точки в данный момент времени.

7) Начальная фаза j₀ − указывает местоположение колеблющейся точки в момент времени t = 0.

5.2. Сложение одинаково направленных и взаимно перпендикулярных гармонических колебаний

Сложение нескольких колебаний одинакового направления можно изображать графически с помощью метода векторной диаграммы.

Гармоническое колебание может быть представлено графически с помощью вращающегося вектора амплитуды 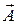. Для этого из произвольной точки О, выбранной на оси Ох, под углом j₀, равным начальной фазе колебания, откладывается вектор амплитуды 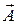. Модуль этого вектора равен амплитуде рассматриваемого колебания. Если этот вектор привести во вращение с угловой скоростью w, равной циклической частоте колебаний, то проекция конца вектора амплитуды будет перемещаться по оси Ох и принимать значения от – А до + А, а колеблющаяся величина изменяться со временем по закону x = A cos(w t + j₀).

1. Сложение одинаково направленных гармонических колебаний.

Сложим два гармонических колебания одинакового направления и одинаковой частоты. Смещение x колеблющегося тела будет суммой смещений x ₁ и x ₂, которые запишутся следующим образом:

x ₁ = A ₁ cos(w t + j₁) и x ₂ = A ₂ cos(w t + j₂). (5.2.1)

Представим оба колебания на векторной диаграмме. Построим по правилу сложения векторов результирующий вектор 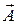. Проекция этого вектора на ось Ох равна сумме проекций слагаемых векторов x =
= x ₁ + x ₂, следовательно, вектор 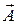представляет собой результирующее колебание. Определим результирующий вектор амплитуды 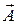по теореме косинусов

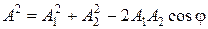. (5.2.3)

Так как угол между векторам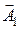и и 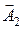равен j = p − (j₂ − j₁), то cos[p − (j₂ − j₁)] = −cos(j₂ − j₁), следовательно, результирующая амплитуда колебания будет равна

. (5.2.4)

Определим начальную фазу результирующего колебания.

Из рисунка видно, что начальная фаза результирующего колебания

. (5.2.5)

Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, также совершает гармонические колебания в том же направлении и с той же частотой.

2. Сложение взаимно перпендикулярных гармонических колебаний.

Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты, происходящих во взаимно перпендикулярных направлениях. Допустим, что материальная точка совершает колебания как вдоль оси X, так и вдоль оси Y. Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний примут вид

x = A ₁ cosw t, и y = A ₂ cos(w t + j), (5.2.6)

где j − разность фаз обоих колебаний.

Уравнение траектории получим, исключив из уравнений (5.2.6) параметр времени t: 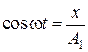, а 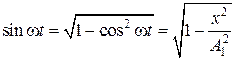. Разложим косинус во втором из уравнений (5.2.6)

cos(w t + j) = cosw t · cosj + sinw t · sinj. (5.2.7)

Тогда

. (5.2.8)

Перепишем это уравнение в следующем виде

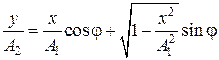Þ 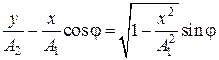. (5.2.9)

После преобразования, получим

. (5.2.10)

Используя тригонометрическое тождество cos² j + sin² j = 1, окончательно получим

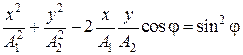. (5.2.11)

Это есть уравнение эллипса, оси которого ориентированы
относительно координатных осей произвольно. Ориентация эллипса и величина его полуосей зависят от амплитуд колебаний и разности фаз.

Рассмотрим несколько частных случаев и определим форму траектории для них:

а) разность фаз равна нулю [j = 0].

В этом случае , откуда получается уравнение прямой

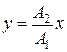. (5.2.12)

Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой w и амплитудой .

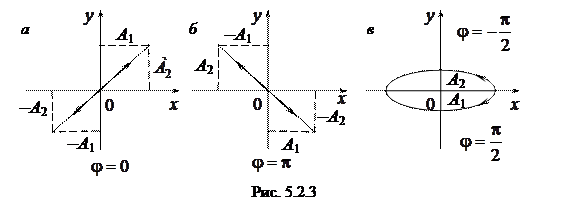2) разность фаз равна ±p [j = ±p].

В этом случае 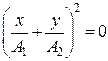, откуда получается уравнение прямой

. (5.2.13)

3) Разность фаз равн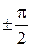а . Тогда

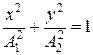. (5.2.14)

Уравнение эллипса, причем полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд колебаний эллипс вырождается в окружность. Случаи и 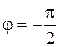отличаются направлением движения. Если , то уравнения колебаний имеют следующий вид: x = A ₁ cosw t, и y = − A ₂ sinw t и движение совершается по часовой стрелке. Если 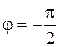, то уравнения колебаний имеют следующий вид: x = A ₁ cosw t, и y = A ₂ sinw t и движение совершается против часовой стрелке.

Рассмотренные три частных случая представлены на рис. 5.2.3, а, б, в.

4) Если частоты складываемых взаимно перпендикулярных колебаний различны, то траектория результирующего движения имеет вид сложных кривых, называемых фигурами Лиссажу. Форма этих кривых определяется соотношением амплитуд, частот и разности фаз складываемых колебаний.

На рис. 5.2.4 показаны фигуры Лиссажу, которые получаются при соотношении частот 1:2 и различной разности фаз колебаний.

По виду фигур можно определить неизвестную частоту по известной частоте или определить соотношение частот складываемых колебаний.

Дата добавления: 2014-01-07