
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Энергия гармонических колебаний
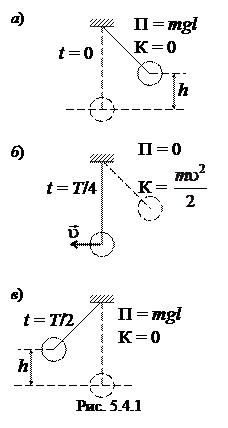 В процессе колебаний происходит превращение кинетической энергии в потенциальную энергию и обратно (рис. 5.4.1). В момент наибольшего отклонения от положения равновесия полная энергия состоит только из потенциальной энергии, которая достигает своего наибольшего значения. Далее при движении к положению равновесия потенциальная энергия уменьшается, при этом кинетическая энергия возрастает. При прохождении через положение равновесия полная энергия состоит лишь из кинетической энергии, которая в этот момент достигает своего наибольшего значения. Далее при движении к точке наибольшего отклонения происходит уменьшение кинетической и увеличение потенциальной энергии. И при наибольшем отклонении потенциальная опять максимальная, а кинетическая энергия рана нулю. И т. д.
В процессе колебаний происходит превращение кинетической энергии в потенциальную энергию и обратно (рис. 5.4.1). В момент наибольшего отклонения от положения равновесия полная энергия состоит только из потенциальной энергии, которая достигает своего наибольшего значения. Далее при движении к положению равновесия потенциальная энергия уменьшается, при этом кинетическая энергия возрастает. При прохождении через положение равновесия полная энергия состоит лишь из кинетической энергии, которая в этот момент достигает своего наибольшего значения. Далее при движении к точке наибольшего отклонения происходит уменьшение кинетической и увеличение потенциальной энергии. И при наибольшем отклонении потенциальная опять максимальная, а кинетическая энергия рана нулю. И т. д.
Потенциальная энергия тела, совершающего гармонические колебания равна
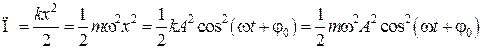 . (5.4.1)
. (5.4.1)
Кинетическая энергия тела, совершающего гармонические колебания равна
 . (5.4.2)
. (5.4.2)
Таким образом, полная энергия гармонического колебания, состоящая из суммы кинетической и потенциальной энергий, определяется следующим образом
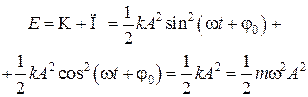 . (5.4.3)
. (5.4.3)
Следовательно, полная энергия гармонического колебания
 . (5.4.4)
. (5.4.4)
оказывается постоянной в случае гармонических колебаний.
Найдем среднее значение потенциальной энергии за период колебания
 . (5.4.5)
. (5.4.5)
Аналогично получается для среднего значение кинетической энергии
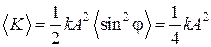 . (5.4.6)
. (5.4.6)
Таким образом, и потенциальная, и кинетическая энергии изменяются относительно своих средних значений по гармоническому закону с частотой 2w и амплитудой  .
.
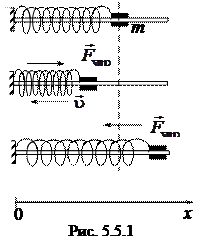 5.5. Пружинный, математический и физический маятники
5.5. Пружинный, математический и физический маятники
Рассмотрим несколько простейших систем, совершающих свободные гармонические колебания.
1) Пружинный маятник − это материальная точка массой m, подвешенная (или расположенная горизонтально) на абсолютно упругой пружине жесткостью k и совершающий гармонические колебания под действием упругой силы. Пусть шайба массой m, прикрепленная к пружине, совершает колебания. Для составления дифференциального уравнения колебаний запишем второй закон Ньютона в проекции на ось Oх F упр = ma. Упругая сила F упр = − kx. Приравнивая последние два уравнения и, используя определение ускорения тела, получим
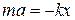 или
или  . (5.5.1)
. (5.5.1)
Отсюда
 . (5.5.2)
. (5.5.2)
Сравнивая уравнения (5.3.7) и (5.5.2) получаем, что пружинный маятник совершает гармонические колебания с частотой
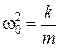 Þ
Þ  . (5.5.3)
. (5.5.3)
Так как период колебаний определяется по формуле  , то период колебаний пружинного маятника
, то период колебаний пружинного маятника
 . (5.5.4)
. (5.5.4)
 2) Математический маятник − это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена материальная точка массой m. Отклонение маятника от положения равновесия будем характеризовать углом j, образованным нитью с вертикалью.
2) Математический маятник − это идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешена материальная точка массой m. Отклонение маятника от положения равновесия будем характеризовать углом j, образованным нитью с вертикалью.
При отклонении маятника от положения равновесия возникает вращательный момент 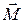 , равный по величине mgl sinj. Он имеет такое же направление, что стремится вернуть маятник в положение равновесия. Следовательно, выражение для
, равный по величине mgl sinj. Он имеет такое же направление, что стремится вернуть маятник в положение равновесия. Следовательно, выражение для
вращательного момента имеет вид: M =
= − mgl sinj. Применим основное уравнение динамики вращательного движения
M = I e, (5.5.5)
где I = ml 2 − момент инерции материальной точки. Тогда, учитывая, что угловое ускорение  , получим
, получим
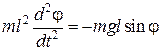 Þ
Þ 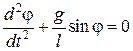 . (5.5.6)
. (5.5.6)
Если рассматривать малые колебания, то  . Получим
. Получим
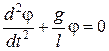 Þ
Þ  . (5.5.7)
. (5.5.7)
То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой
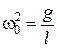 Þ
Þ  . (5.5.8)
. (5.5.8)
Период колебаний математического маятника
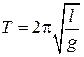 . (5.5.9)
. (5.5.9)
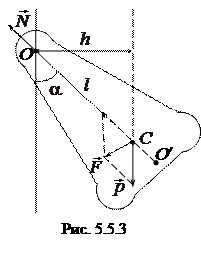 3) Физический маятник − это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, проходящей через точку, не совпадающую с центром масс тела. При отклонении маятника от положения равновесия на угол j возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен M = − mgl sinj.
3) Физический маятник − это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной оси, проходящей через точку, не совпадающую с центром масс тела. При отклонении маятника от положения равновесия на угол j возникает вращательный момент, стремящийся вернуть маятник в положение равновесия. Этот момент равен M = − mgl sinj.
Согласно основному уравнению динамики вращательного движения получаем
 Þ
Þ 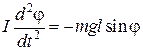 , (5.5.10)
, (5.5.10)
где I − момент инерции маятника относительно оси, проходящей через точку подвеса.
Если рассматривать малые колебания, то  . Получим
. Получим
 Þ
Þ  . (5.5.11)
. (5.5.11)
То есть при малых колебаниях угловое отклонение математического маятника изменяется по гармоническому закону с частотой
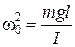 Þ
Þ 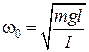 . (5.5.12)
. (5.5.12)
Период колебаний математического маятника
 . (5.5.13)
. (5.5.13)
Из сопоставления формул периодов колебаний математического и физического маятников 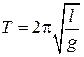 и
и  получается, что математический маятник с длиной
получается, что математический маятник с длиной
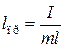 . (5.5.14)
. (5.5.14)
будет иметь такой же период колебаний, что и данный физический маятник.
Величина l пр (отрезок OO ¢) называется приведенной длиной физического маятника − это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка на прямой, соединяющей точку подвеса с центром масс, и лежащая на расстоянии приведенной длины от оси вращения, называется центром качания (О ¢) физического маятника. Точка подвеса О и центр качания обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.
|
Дата добавления: 2014-01-07; Просмотров: 1552; Нарушение авторских прав?; Мы поможем в написании вашей работы!