Достаточность

Необходимость доказана.

Доказательство будем проводить для случая 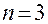. Это доказательство легко распространяется на случай .

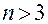При 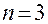функции 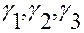зависят от трех переменных :

,

,

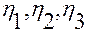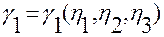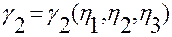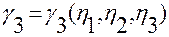
и являются непрерывно дифференцируемыми по этим переменным в области .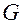

Покажем, что если выполнены условия (2.3.7), то можно построить такую непрерывно дифференцируемую функцию 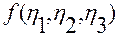в некоторой области , для которой будет выполняться

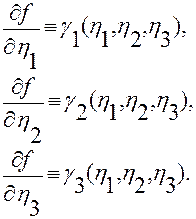(2.3.13)

Если это будет доказано, то из непрерывной дифференцируемости функции 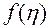следует существование полного дифференциала 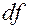этой функции

,

а из тождеств (2.3.13) — его совпадение с левой частью уравнения (2.3.5):

.

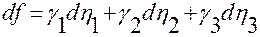Итак, докажем существование такой функции .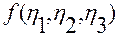

Зафиксируем любую точку 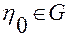и выберем ограниченную область 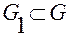, которая содержит эту точку. Положим

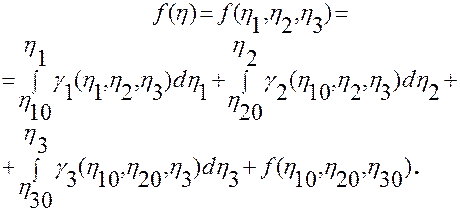
Здесь интегрирование осуществляется по каждой координате 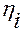, , 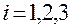вне зависимости от значений двух других координат , , .

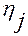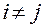Кроме того, 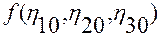— это произвольно выбранное фиксированное значение функции 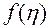в точке .

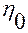Очевидно, функция 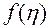определена и непрерывна по совокупности переменных 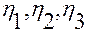в некоторой области 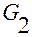, целиком содержащейся в области .

Такой областью 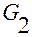, например, является параллелепипед с гранями, параллельными соответствующим координатным осям 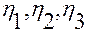, вписанный в область и содержащий точку .

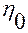Из вида функции 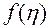заключаем, что она непрерывно дифференцируема по переменным 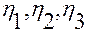, поскольку интегралы непрерывно дифференцируемы по верхнему пределу, подынтегральные функции непрерывно дифференцируемы по параметрам, и интегралы берутся по ограниченному промежутку изменения переменных (ибо область 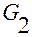ограничена).

Вычислим 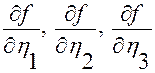в любой точке 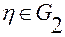и покажем, что для них справедливы тождества (2.3.13) при любом 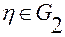. Очевидно, при 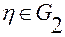будем иметь

,

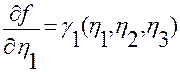т.е. справедливо первое тождество в (2.3.13).

Покажем справедливость второго тождества в (2.3.13). Согласно правилу Лейбница – правилу вычисления производной интеграла, зависящего от параметра [см. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.2, М.: Наука, 1969, стр.661], при 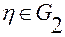можем записать:

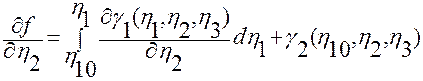. (2.3.14)

Воспользуемся тождеством (2.3.7)

.

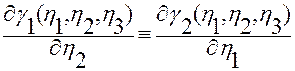Записанное для функци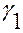й и 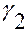, это тождество справедливо для всех 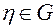, а значит, и для всех .

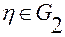Заменим подынтегральное выражение в (2.3.14) правой частью тождества.

.

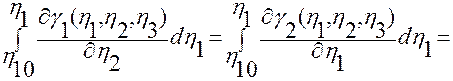
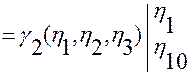
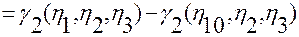Результат вычисления интеграла подставим в правую часть формулы (2.3.14):

.

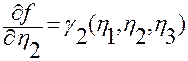Данное равенство справедливо при любом 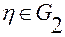. Этим доказали справедливость второго тождества в (2.3.13).

Докажем справедливость третьего тождества в (2.3.13). Применим правило Лейбница при вычислении .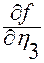

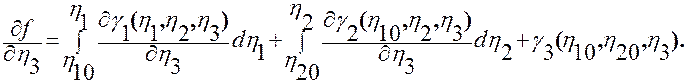
Учитывая тождества (2.3.7)

, ,

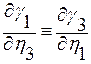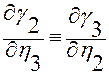и заменяя подынтегральные выражения правыми частями этих тождеств, получим

.

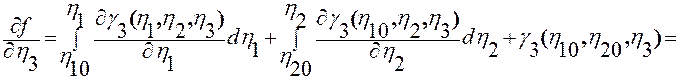
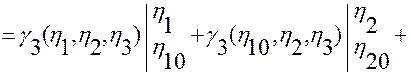
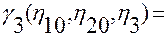
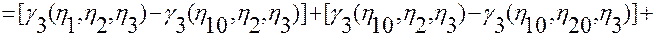
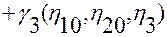Отсюда следует:

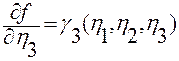для .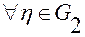

Теорема доказана.

2. Дополнение 2 к п.3 §3 (к стр. 10 лекции)

Дата добавления: 2014-01-07