Хаос в простых моделях динамических систем

«Период три означает хаос» и теорема Шарковского. Как мы упоминали, в 1975 г. Американские математики Ли и Йорке опубликовали ставшую широко известной работу «Period three implies chaos». Ока­зывается, что если у одномерного отобра­женияесть цикл периода три, то оно имеет континуум непериоди­ческих траекторий. Единственное требо­вание к функциисостоит в том, что она должна быть непрерывной.

Пусть а, b, с — три элемента цикла: b = f (а), с = f(b), а = /(с), и а — ми­нимальный из них. (Заметим, что ника­кие два элемента не могут совпадать, так как в этом случае цикл выродился бы в неподвижную точку.) Возможны два слу­чая: b < с и b > с, из которых обсу­дим только первый (второй анализируется аналогично). Рассмотрим специальный пример — кусочно-линей­ное отображение, показанное на рис. 2.5. Правило, определяющее его динамику в обратном времени, можно сформулировать так:

(а) если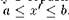 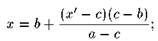, то положить

(б) еслито выбрать один из двух вариантов,

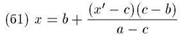
или

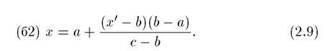
Будем строить траекторию в обратном времени по этим правилам. Заметим, что если на некотором шаге возникла ситуация (а), то на следующем шаге обязательно реализуется ситуация (б). Каждый раз, встретившись с ситуацией (б), будем делать выбор с помощью случайных испытаний, скажем, бросанием монеты: орел — (б1), решка — (б2). Получится хаотическая траектория. Ясно, что ее можно наблюдать и при динамике в прямом времени при задании некоторого вполне определенного начального условия.

А теперь заметим, что на самом деле конкретный вид отобра­жения (2.9) непринципиален, важно лишь то, что точки интервала 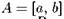имеют прообразы в интервале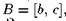а точки интервала B имеют прообразы и в А, и в В. Э того достаточно, чтобы у отображения наличествовало подмножество траекторий, кодиру­емых по тем же правилам, как траектории отображения (2.9).

Наряду с континуумом хаотических траекторий непрерывное одномерное отображение, у которого есть цикл периода три, имеет также циклы всевозможных периодов. Это частный случай тео­ремы Шарковского (Шарковский, 1964), содержание которой со­стоит в следующем:

Если непрерывное отображение одномерного интервала в себя имеет цикл периода т, то оно имеет также и циклы со всевозможными периодами m ', предшествующими числу т в перечне всех целых чисел, выписанных в так называемом по­рядке Шарковского:

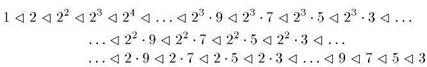
2.2. Двумерные отображения, сохраняющие площадь

Отображение пекаря. Давайте попытаемся построить отображе­ние, отправляясь от рассмотрения динамики типа сдвига Бернулли на множестве последовательностей бесконечных в обе стороны. Запишем такую последовательность в виде

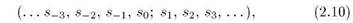
где каждое s_i- есть либо 0, либо 1. Обратите внимание на особый разделительный символ — точку с запятой, который встречается в одном-единственном месте; его присутствие позволяет соотносить положение символов с некоторым «началом отсчета». Введем двединамические переменные — действительные числа ж и у, при­надлежащие единичному интервалу, определив их через символы S_i следующим образом:

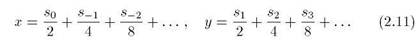
Пусть трансформация последовательности (2.10) за один времен­ной шаг состоит в том, что все символы сдвигаются на одну по­зицию вправо, так что результатом окажется

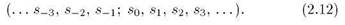
Тогда новые значения x и y будут

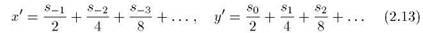
Их можно выразить через старые значения ж и у следующим обра­зом:

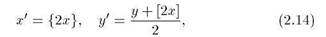
где фигурные скобки обозначают дробную часть числа, а квадрат­ные — целую часть. Другая форма записи тех же соотношений:

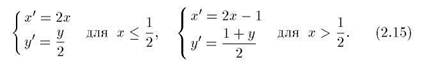
По самому своему построению наша система может демонстри­ровать хаотическую динамику: чтобы получить хаос нужно взять в качестве последовательности (2.10) случайный набор символов. Система имеет также бесконечное множество периодических орбит (циклов) — им отвечают периодические последовательности.

В отличие от примеров, приведенных в предыдущем разделе, мы пришли к двумерному отображению, описывающему дина­мику в терминах переменных ж и у. Мгновенное состояние на­шей системы определяется заданием этих двух величин, причем обе они необходимы для того, чтобы иметь возможность находить последующие состояния по известному начальному.

Можно ли представить себе действие двумерного отображения в наглядной геометрической форме? Такое представление суще­ствует, и именно оно послужило основанием назвать данную мо­дель отображением пекаря. (В литературе на английском языке оно обозначается как Baker's map. He надо думать, что это ото­бражение имени некоего ученого по фамилии Бейкер!)

Рассмотрим единичный квадрат на плоскости (ж, у). Разре­заем его пополам, как кусок теста, накладываем одну половинкуна другую и раскатываем так, чтобы восстановить исходную форму (рис. 2.6). Для наглядности «тесто», оказавшееся слева при пер­вом разрезе, изображено темным, а справа — светлым. На ри­сунке показано, как выглядит распределение темного и светлого теста на нескольких последовательных шагах. При большом чи­сле итераций это распределение принимает вид набора тонких и длинных чередующихся темных и светлых полосок. При много­кратном повторении процедуры в конце концов получаем кусок те­ста, который выглядит однородным. Взяв для пробы небольшой кусочек, мы обнаружим в нем присутствующие в равных долях

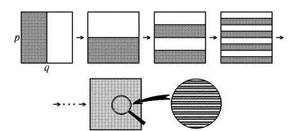
Рис. 2.6. Геометрическая иллюстрация действия отображения пекаря (2.15). В верхней части рисунка показаны три шага последовательных итераций отобра­жения, а внизу — состояние, возникшее после некоторого достаточно большого числа итераций

темную и светлую составляющие. Описанное свойство отображе­ния пекаря называется именно так, как мы его и назвали бы на «бытовом» языке, — перемешивание.

Отображение пекаря является консервативной системой или, используя терминологию, специфическую для двумерных отобра­жений, это отображение, сохраняющее площадь. Если взять некоторую область на плоскости (ж, у) и подвергнуть каждую ее точку действию отображения пекаря, то она перейдет в некото­рую другую по форме область, но площадь новой области останется той же самой. Формальное правило для проверки этого свойства состоит в том, что должен равняться единице определитель, по­строенный из производных, — якобиан. Для отображения пекаря имеем:

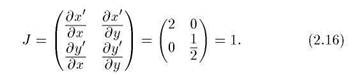
В более широком контексте вместо «площадь» говорят «мера». В случае двумерного фазового пространства мера — это площадь, в случае одномерного — длина, в случае трехмерного — объем.Мы уже интерпретировали представленную на рис. 2.6 динамику как перемешивание слоев двух сортов теста или, если угодно, двух жидкостей — темной и светлой. Сохранение меры отвечает тому, что эти жидкости являются несжимаемыми.

Отображение «кот Арнольда». Рассмотрим двумерное отображе­ние

которое называют отображением кота Арнольда (Arnold's cat map). Причиной для такого названия послужило то, что пред-

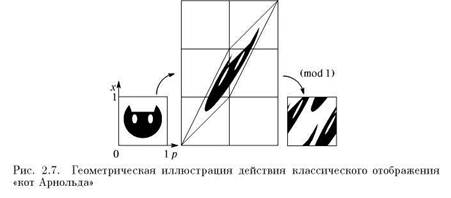
ложивший это отображение В.И.Арнольд использовал для иллю­страции его действия изображение кота (рис. 2.7). Геометрически первый шаг процедуры состоит в линейном преобразовании ко­ординат, а второй — в переносе элементов

картинки,удалившихся за рамки единичного квадрата, обратно в него. Последнее отвечает, конечно, операции взятия модуля, бла­годаря присутствию которой фазовое пространство можно считать периодическим по обеим динамическим переменным р и х и ин­терпретировать как поверхность тора. Впрочем, для наглядного графического представления динамики удобнее использовать про­сто единичный квадрат, как на рис. 2.7.

Как и отображение пекаря, отображение кота Арнольда отно­сится к классу консервативных динамических систем. Матема­тически это выражается в том, что детерминант матрицы М =

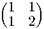= , задающей отображение, равен 1, и оно, следовательно,

сохраняет меру (площадь) любой области, например, изображения кота.Можно рассмотреть более широкий класс линейных отображе­ний на торе, определяемых всевозможными матрицами 2 X 2 с целочисленными элементами и единичным определителем:

В зависимости от собственных чисел матрицы, которые нахо­дятся из решения квадратного уравнения

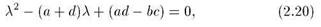
отображения вида (2.18) относятся к одному из трех типов:

• гиперболический, если одно из собственных чисел больше, а второе меньше 1;

• параболический, если

• эллиптический, есликомплексно-сопряженные. Отображение кота Арнольда принадлежит к гиперболическому

типу, поскольку его собственные числа: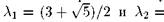

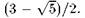=При итерациях этого отображения закрашенная

область (изображение кота) вытягивается вдоль направления пер­вого (неустойчивого) собственного вектора на каждом шаге в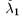раз и сжимается вдоль второго (устойчивого) собственного напра­вления, соответственно, враз. После достаточно большого чи­сла итераций изображение кота превращается в чрезвычайно уз­кую полосу, вытянутую вдоль неустойчивого собственного напра-

Рис. 2.8. Динамика отображения «кот Арнольда» в течение пяти шагов итераций. Обратите внимание на быстро развивающийся процесс перемешивания

вления, т. е. близкую к длинному отрезку линии, заданной урав­нением р = [(л/5 — 1)/2]ж (modi). Из-за того что угловой ко­эффициент иррационален, эта линия покрывает поверхность тора всюду плотно. Поэтому картина выглядит как набор большого числа узких чередующихся черных и белых полосок, в которые превратились, соответственно, множество точек, принадлежащих изображению кота, и дополнение этого множества: черная и бе­лая «жидкости» оказываются хорошо перемешанными (рис. 2.8). Это свойство перемешивания аналогично тому, которое отмечалось для отображения пекаря. Оно строго доказывается в своей точной математической формулировке для гиперболических отображений на торе и служит основанием для заключения о хаотической дина­мике этих систем. В частности, из перемешивания следует свой­ство эргодичности, которое состоит в том, что вычисление ста­тистических средних по ансамблю эквивалентно усреднению по времени вдоль типичной индивидуальной траектории.

Дата добавления: 2014-01-07