Оценка называется точечной, если в результате оценивания получается значение неизвестного параметра в виде числа

Типы оценок

Оценки бывают двух типов – точечные и интервальные.

Например, точечной оценкой математического ожидания μ(х) является среднее значение случайной величины 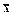=3,14.

Точечная оценка является функцией от элементов выборки:

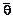= g(x₁,x₂ ... x_N).

Например, то же среднее арифметическое

.

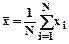Оценка называется интервальной, если в результате оценивания получаются границы интервала, внутри которого с определенной вероятностью находится значение искомого параметра: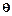

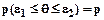
На рисунке 9.2 показана графическая интерпретация интерваль-ного оценивания.

9.2 – Интервальное оценивание

Интервал называется доверительным интервалом, его нижняя и верхняя границы называются соответственно нижним и верхним доверительными пределами, а вероятность р – доверительной вероятностью. Т.о. при интервальном оценивании находится интервал, в котором с заданной доверительной вероятностью находится параметр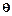,причем центром этого интервала является точечная оценка .

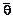Статистическое оценивание будет полным, если найдены как точечная, так и интервальная оценки исследуемого параметра.

Например, точечная и интервальная оценки роста некоторой совокупности людей (рис.7.3):

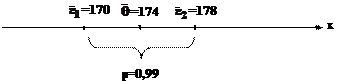Рисунок 7.3 – Полная оценка роста

Дата добавления: 2014-01-07