Лекция10. Численное моделирование деформации полотна термоэластопласта методом одиночной поры

Вычислим изменение размеров поры при растяжении полотна ТЭП, расположенного вдоль оси 0Y, при этом оси 0Х совпадает с нейтральной осью полотна, т.е. проходит по середине полотна.

Рассмотрим элемент этого продольного полотна, расположенный между двумя плоскостями a₁b₁ и а₂b₂ и имеющий до деформации площадь поперечного сечения S, а после деформации S - ΔS.

Обозначим, через R радиус кривизны поры. Тогда,

(y>0)

(10.1)

Поэтому, используя закон Гука для растяжения и определенными λ, получим формулу (10.2)

(10.2)

где Е - модуль упругости Юнга.

Зная напряжения, действующие в рассматриваемом сечении, можно вычислить изгибающий момент М:

(10.3)

Если изгибающий момент в каждом сечении известен, можно найти величину λ и составить дифференциальное уравнение изогнутой оси поры по формуле (10.4):

,

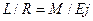
(10.4)

Когда прогиб поры мал, то величину 1/R можно заменить на 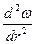, тогда дифференциальное уравнение состояния деформированной поры запишется в виде (10.5):

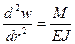
(10.5)

Величина λ и прогиб поры зависят явно лишь от изгибающего момента. Непосредственно от величины перерезывающей силы зависят касательные напряжения в поперечном сечении, которые, как правило, при изгибе бывают менее существенными, чем нормальные напряжения.

При статической нагрузке момент М не зависит от времени, и временное изменение объема полотна определяют упругость петли. Считая в нашем случае нагружение меняющимся с постоянной скоростью, т. е. можно записать, что изгибающий момент М = αТ. В этом случае уравнение, описывающее изменение объема полотна с учетом внутреннего трения, будет иметь вид (10.6):

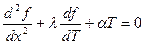
(10.6)

где λ - коэффициент внутреннего трения; α - скорость изменения нагрузки.

Рассмотрим численные расчеты изменения объема полотна от времени согласно (10.6), выполненные с помощью интегрированной среды MCAD 2009.

Представлено линейное дифференциальное уравнение 2-го порядка частных производных (10.6) при следующих начальных и граничных условиях: τ = 0.08; h = 0.8; x = 1..45; t = 1.50; α = 0.1;1;5; Λ = 0.1;0.5;1;5;9;13;17;21;25; f_0,x=0; f_0.0=1; f_0.10=3;f_0.50=0.5.

В начальных условиях полагаем на первом этапе отсутствие деформации полотна. В настоящей задаче требуется найти неизвестную функцию f (x, t).

Для решения уравнения и определения f (x, t) применим конечно-разностный сеточный трехслойный метод. Зададимся сеткой с узлами в точках (t, x) и заменим исходную дифференциальную задачу разностной.

Рассмотрим трехслойную схему, аппроксимирующую исходные дифференциальные операторы системы с погрешностью 0 (h² +т²):

	(10.7)

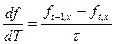
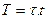
где h - шаг по оси х;

τ - шаг по времени;

х - количество узлов по оси х; t.

Количество узлов по оси у:

Подставив исходные операторы в дифференциальное уравнение получаем:

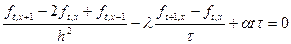
(10.8)

Решаем конечно-разностное уравнение относительно f (t, x). Получаем разностную схему для исходной задачи:

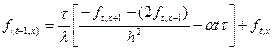
(10.9)

Предложенная численная схема устойчива при о ≤ vτ / h ≤ 1.

В ходе проведенных компьютерных расчетов исследовалось изменение объема полимерного полотна.

Рассмотрим влияние вязкости и скорости стеклования на деформацию. При малых скоростях α = 0.1 и малых вязкостях λ = 0.1;0.5 деформация в начальной координате практически не возникает, однако с ростом длины деформация резко увеличивается, может быть до разрыва.

С увеличением вязкости λ процесс деформации носит осцилирующий характер, при этом поле осциляции увеличивается с ростом координаты х. Однако при больших λ деформации возникают в момент t = 0 и затухают, а поле осциляции сужается. При больших временах t система возвращается в исходную ситуацию.

Аналогичный процесс наблюдается при α = 1. При α = 5 и более на осциляции накладывается статическая деформация полотна. Характер изменения статической деформации имеет вид параболы. Здесь при малых λ, = 0.5 имеет место осциляция в начальный момент времени t они затухают и в последствии развиваются вновь. Когда λ, возрастает осциляция локализуется на фоне параболической деформации.

СЛУЧАЙ 1

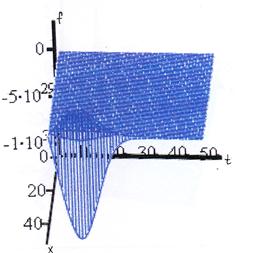
Рис.10.1.Зависимость степени деформации полотна от времени и координат при α=0.1, λ=0.1

Рис.10.2. Зависимость степени деформации полотна от времени и координат при α=0.1, λ=0.5

Откуда берутся нанопоры? За счет перекрестной сшивки, т.е сшивки перпендикулярной длине молекул. Об этом свидетельствует рентгено-структурный анализ 1,2-СПБ-9, JSRB, анализ ИК-спектров.

В связи с этим рассмотрим результаты этих исследований:

а)рентгено-структурный анализ;

б) ИК-спектроскопию;

в) Задачу равновесия трещин в упругой среде.

Рентгеноструктурный анализ. С целью выяснения влияния УФ облучения на кристаллическую структуру 1,2-СПБ были сняты соответствующие рентгенограммы исходного и облученного полимера (рис.10.3). Полученная рентгенограмма исходного образца 1,2-СПБ наряду с интенсивным амор- фным гало имеет характерные пики,отвечающие размерам элементарной ячейки кристалла: a=1.094 нм, b=0.655 нм и с=0.419 нм (таблица 10.1), что

хорошо согласуются с литературными данными.

При облучении 1,2-СПБ в его кристаллической области происходит преимущественно диагональное межмолекулярное сшивание, о чём свидетельствует разрушение структуры

кристаллической области по а и по b осям – уменьшение (010),(110) и (210).

Степень кристалличности понижается с 18 до 13%.

Рис.10.4. Рентгенограмма образца 1,2-СПБ: 1-исходного,2-облученного УФ светом 30 мин. Стрелками показано изменение интенсивности характерных рефлексов

Таблица 10.1.

Результаты рентгеноструктурного анализа 1,2 СПБ

ИК-спектроскопия. В полученном ИК спектре плёнки 1,2-СПБ (рис.10.5,кривая 1) чётко и интенсивно вырисовываются характеристические

полосы поглощения деформационных колебаний связей С-Н в структурах (910 см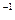), хорошо выражена полоса валентных колебаний двойных С=С связей в области 1640см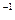. Интенсивная полоса при 1430см-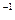обусловлена

деформационными колебаниями метильных групп, что достаточно хорошо

согласуется с литературными данными.

При УФ облучении на воздухе, каких в указанных выше работах, происходят интенсивное сшивание и окисление полимера (рис.10.5, кривые 2 и 3). По ИК спектрам облученного УФ 60 мин 1,2-СПБ заметно разрушение двойных связей: уменьшаются интенсивности частот колебаний в области 1000см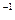,1450 см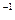и 2900 см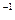(рис.10.5,↓) и появляются частоты колебаний кислородных групп (карбонильных -1720см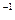и, по-видимому, карбоксильных -3400см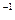) (рис.10.5,↑).

Таким образом, фотохимическая дезактивация в присутствии кислорода воздуха является очень существенной.

Рис.10.5. ИК спектры 1,2-СПБ: 1- исходного, 2-облученного УФ светом 30 мин, 3-облученного УФ светом 60 мин. Стрелками показано изменение интенсивности характерных сигналов и появление новых

По ИК спектрам облученного УФ 60 мин 1,2-СПБ заметно разрушение двойных связей: уменьшаются интенсивности частот колебаний в области

1000 см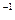, 1450см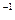и 2900см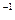(рис.10.5,↓) и появляются частоты колебаний

кислородных групп (карбонильных -1720 см^-1 и по-видимому карбоксильных -3400см) (рис.10.5, ↓).

Дата добавления: 2014-01-07