
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Комбинированные методы разработки управленческих решений 2 страница
В основе формализованных методов разработки решений лежит научно-практический подход, предполагающий выбор оптимальных решений с помощью ЭММ и ЭВМ.
К формализованным можно отнести и статические методы. Они основаны на использовании информации о прошлом опыте организаций в какой-либо сфере деятельности для разработки или реализации управленческих решений и реализуются путем сбора, обработки и анализа статических материалов как полученных в результате реальных действий, так и выработанных искусственно, путем статического моделирования на ЭВМ.
В таблице 2 представлена характеристика формализованных методов разработки управленческих решений.
Таблица 2
Формализованные методы разработки управленческих решений
| № п/п | Наименование метода | Краткая характеристика методов решения | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Балансовый метод | Метод который позволяет произвести балансовые сопоставления, увязки. Например, сопоставляются: расход и приход, затраты и прибыль и выбирается наиболее прибыльный вариант Балансовый метод применяют также при проверке расчётов, произведённых другими специальными аналитическими методами. Балансовый метод анализа хозяйственной деятельности служит, главным образом, для отражения соотношений, пропорций двух групп взаимосвязанных и уравновешенных экономических показателей, итоги которых должны быть тождественными. Этот метод широко распространен в практике бухгалтерского учета и планирования. Но определенную роль он играет и в анализе хозяйственной деятельности. Он широко используется при анализе обеспеченности предприятия трудовыми, финансовыми ресурсами, сырьем, топливом, материалами, основными средствами производства и т.д., а также при анализе полноты их использования. Определяя, например, обеспеченность предприятия трудовыми ресурсами, составляют баланс, в котором, с одной стороны, показывается потребность в трудовых ресурсах, а с другой стороны – фактическое их наличие. При анализе использования трудовых ресурсов сравнивают возможный фонд рабочего времени с фактическим количеством отработанных часов, определяют причины сверхплановых потерь рабочего времени Для определения платежеспособности предприятия составляется платежный баланс, в котором соотносятся платежные средства с платежными обязательствами. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Метод Гаусса | Последовательное изменение состава опорного решения до получения оптимального варианта, недопускающего улучшения. Это способ решения оптимизационной задачи, у которой оценка и ограничения являются линейными функциями
Ме́тод Га́усса[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.
· На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
· На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Метод Гаусса требует  арифметических операций.
Пример
Покажем, как методом Гаусса можно решить следующую систему: арифметических операций.
Пример
Покажем, как методом Гаусса можно решить следующую систему:
 Обнулим коэффициенты при
Обнулим коэффициенты при 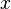 во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на во второй и третьей строчках. Для этого вычтем из них первую строчку, умноженную на 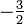 и и 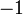 , соответственно: , соответственно:
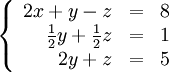 Теперь обнулим коэффициент при
Теперь обнулим коэффициент при 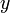 в третьей строке, вычтя из неё вторую строку, умноженную на в третьей строке, вычтя из неё вторую строку, умноженную на 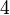 : :
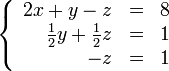 В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
 из третьего; из третьего;
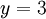 из второго, подставив полученное из второго, подставив полученное 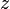
 из первого, подставив полученные из первого, подставив полученные 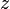 и и 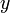 .
Таким образом исходная система решена.
В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.
Применение и модификации
Помимо аналитического решения СЛАУ, метод Гаусса также применяется для: .
Таким образом исходная система решена.
В случае, если число уравнений в совместной системе получилось меньше числа неизвестных, то тогда ответ будет записываться в виде фундаментальной системы решений.
Применение и модификации
Помимо аналитического решения СЛАУ, метод Гаусса также применяется для:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
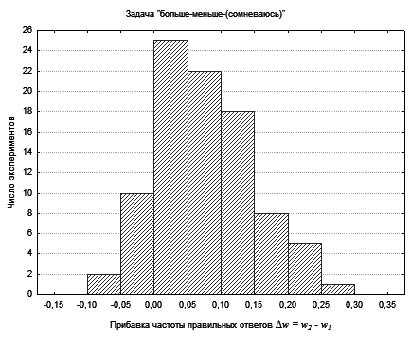
| Гистограмма | Иллюстрация частоты появления отдельных значений параметра выполняется в виде гистограммы. В ней для каждого значения параметра (по горизонтали) показывается (по ординате) число соответствующих случаев их или их доля в общей доле случаев. На гистограмме отражаются частота появления средних значений, диапазон разброса значений. Могут быть выбраны разные варианты решений, но чаще выбираются наиболее вероятные
Слово 'гистограмма' происходит из Греции и состоит из слов 'isto-s' (ιστοs) (= 'столб', также это слово обозначает 'паутину', но это не существенно для нашего обсуждения) и 'gram-ma' (γραμμα) (= 'нечто записанное'). Следовательно, термин следует интерпретировать, как некую форму записи, состоящую из 'столбиков', т.е. продолговатых, вертикально расположенных фигур. Однако это слово изначально не использовалось в греческом языке.1 Термин 'гистограмма' был введен знаменитым статистиком Карлом Пирсоном (Karl Pearson)2 для обозначения "общей формы графического представления". В цитате Оксфордского словаря английского языка из "Philosophical Transactions of the Royal Society of London" Series A, Vol. CLXXXVI, (1895) p. 399" упоминается, что "[Слово 'гистограмма' было] введено автором лекций по статистике как термин для обозначения общей формы графического представления, т.е. путем маркировки столбцов как областей частотности в соответствии с масштабом их базиса". Стинглер отождествляет упомянутые лекции с изданными в 1892 г. лекциями по статистической геометрии [69].
Из всего сказанного ясно, что гистограммы задумывались как визуальная поддержка статистической аппроксимации. Даже сегодня этот смысл доминирует в общем восприятии гистограмм. В словаре Вебстера гистограмма определяется как "столбчатая диаграмма частотного распределения, в которой ширина столбцов пропорциональна классам, на которые была разделена переменная, а высота столбцов пропорциональная частотам этих классов". Однако гистограммы исключительно полезны, даже если отсоединить их от канонического графического представления и рассматривать как чисто математические объекты, сохраняющие приближения распределений данных. Именно так мы относимся к ним в этой статье.
В последние два десятилетия гистограммы использовались в нескольких областях информатики. Кроме области баз данных, гистограммы играют важную роль, главным образом, в областях обработки изображений и машинного зрения. При заданном изображении (или видео) и визуальном пиксельном параметре, гистограмма фиксирует для каждого возможного значения параметра ("класса" по Вебстеру) число пикселей, имеющихся у этого значения ("частота" по Вебстеру). Такая гистограмма является сводной характеристикой изображения и может быть очень полезна при решении нескольких задач: распознавании похожих изображений, сжатии изображений и т.д. В литературе наиболее распространены диаграммы цветов, например, в системе QBIC [21], но было предложено и несколько других параметров, например, плотность границ, текстурность, градиент яркости и т.д. [61]. Вообще говоря, гистограммы, используемые в областях обработки изображений и машинного зрения, являются точными. Например, в гистограмме цветов содержится раздельное и точное число пикселей для каждого возможного отдельного цвета изображения. Единственным элементом аппроксимации могло бы быть число бит, используемых для представления различных цветов: наличие меньшего числа бит означает, что несколько реальных цветов будет изображаться одним цветом, ассоциируемым с числом пикселей, которое имелось бы совместно у всех заменяемых таким образом цветов. Однако даже такая разновидность аппроксимации не является распространенной. В области баз данных гистограммы используются как механизм выровненного по краям сжатия и аппроксимации распределений данных. В литературе и системах они появились в 1980-х и впоследствии изучались с возрастающей интенсивностью. В этой статье мы концентрируемся на понятии гистограмм, принятом в области баз данных, обсуждаем наиболее важные разработки, относящиеся к этой теме, и кратко характеризуем несколько проблем, которые считаем интересными, и решение которых может еще более расширить применимость и полезность гистограмм.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| График изменения во времени | Является наиболее традиционной формой графической иллюстрации, показывающей изменение параметра во времени. На графике с некоторой дискретностью показывается динамика значений параметра, что позволяет выявить интервалы времени, в которые происходило изменение тенденции, и спрогнозировать будущее поведение системы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Двухпараметрический график | Используется для анализа взаимосвязи двух одновременно изменяющихся параметров, рассматриваемые параметры отмечаются по осям координат. Такой график, так же как и временной, может быть дополнен предпочтительными или граничными линиями. Сравнение фактической связи параметров с идеальным графиком позволяет увидеть степень отклонения оцениваемой ситуации от предпочтительной и принять решений по устранению нежелательных отклонений | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дерево влияющих параметров | Является одним вариантом из классификации совокупности влияющих факторов. Корневым элементом дерева принимается анализируемая проблем. Вся совокупность факторов разделяется на группы и подгруппы. Группы показываются как основные «ветви», а подгруппы – как вспомогательные «ветви» дерева. Подобная графическая иллюстрация позволяет наращивать число уровней классификационной детализации до трех-пяти. В результате проблем приобретает системный структурированный вид и иерархии подпроблем, требующий последовательного разрешения
Дерево принятия решений (также могут назваться деревьями классификации или регрессионными деревьями) — используется в области статистики и анализа данных для прогнозных моделей. Структура дерева представляет собой следующее: «листья» и «ветки». На ребрах («ветках») дерева решения записаны атрибуты, от которых зависит целевая функция, в «листьях» записаны значения целевой функции, а в остальных узлах — атрибуты, по которым различаются случаи. Чтобы классифицировать новый случай, надо спуститься по дереву до листа и выдать соответствующее значение. Подобные деревья решений широко используются в интеллектуальном анализе данных. Цель состоит в том, чтобы создать модель, которая предсказывает значение целевой переменной на основе нескольких переменных на входе.
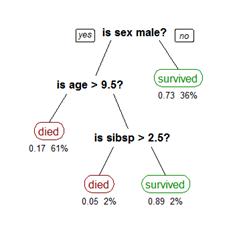 Каждый лист представляет собой значение целевой переменной, измененной в ходе движения от корня по листу. Каждый внутренний узел соответствует одной из входных переменных. Дерево может быть также «изучено» разделением исходных наборов переменных на подмножества, основанные на тестировании значений атрибутов. Это процесс, который повторяется на каждом из полученных подмножеств. Рекурсия завершается тогда, когда подмножество в узле имеет те же значения целевой переменной, таким образом, оно не добавляет ценности для предсказаний. Процесс, идущий «сверху вниз», индукция деревьев решений (TDIDT)[1], является примером поглощающего «жадного» алгоритма, и на сегодняшний день является наиболее распространенной стратегией деревьев решений для данных, но это не единственная возможная стратегия. В интеллектуальном анализе данных, деревья решений могут быть использованы в качестве математических и вычислительных методов, чтобы помочь описать, классифицировать и обобщить набор данных, которые могут быть записаны следующим образом:
Каждый лист представляет собой значение целевой переменной, измененной в ходе движения от корня по листу. Каждый внутренний узел соответствует одной из входных переменных. Дерево может быть также «изучено» разделением исходных наборов переменных на подмножества, основанные на тестировании значений атрибутов. Это процесс, который повторяется на каждом из полученных подмножеств. Рекурсия завершается тогда, когда подмножество в узле имеет те же значения целевой переменной, таким образом, оно не добавляет ценности для предсказаний. Процесс, идущий «сверху вниз», индукция деревьев решений (TDIDT)[1], является примером поглощающего «жадного» алгоритма, и на сегодняшний день является наиболее распространенной стратегией деревьев решений для данных, но это не единственная возможная стратегия. В интеллектуальном анализе данных, деревья решений могут быть использованы в качестве математических и вычислительных методов, чтобы помочь описать, классифицировать и обобщить набор данных, которые могут быть записаны следующим образом:
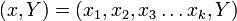 Зависимая переменная Y является целевой переменной, которую необходимо проанализировать, классифицировать и обобщить. Вектор х состоит из входных переменных
Зависимая переменная Y является целевой переменной, которую необходимо проанализировать, классифицировать и обобщить. Вектор х состоит из входных переменных 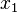 , , 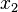 , , 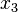 и т. д., которые используются для выполнения этой задачи.
Основные определения
В анализе решений «дерево решений» используются как визуальный и аналитический инструмент поддержки принятия решений, где рассчитываются ожидаемые значения (или ожидаемая полезность) конкурирующих альтернатив.
Дерево решений состоит из трёх типов узлов: и т. д., которые используются для выполнения этой задачи.
Основные определения
В анализе решений «дерево решений» используются как визуальный и аналитический инструмент поддержки принятия решений, где рассчитываются ожидаемые значения (или ожидаемая полезность) конкурирующих альтернатив.
Дерево решений состоит из трёх типов узлов:
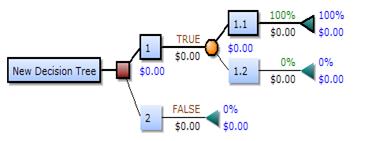 На рисунке, представленном выше, дерево решений следует читать слева направо. Дерево решений не может содержать в себе циклические элементы, то есть каждый новый лист впоследствии может лишь расщепляться, отсутствуют сходящиеся пути. Таким образом, при конструировании дерева вручную, мы можем столкнуться с проблемой его размерности, поэтому, как правило, дерево решения мы можем получить с помощью специализированных софтов. Обычно дерево решений представляется в виде символической схемы, благодаря которой его проще воспринимать и анализировать.
На рисунке, представленном выше, дерево решений следует читать слева направо. Дерево решений не может содержать в себе циклические элементы, то есть каждый новый лист впоследствии может лишь расщепляться, отсутствуют сходящиеся пути. Таким образом, при конструировании дерева вручную, мы можем столкнуться с проблемой его размерности, поэтому, как правило, дерево решения мы можем получить с помощью специализированных софтов. Обычно дерево решений представляется в виде символической схемы, благодаря которой его проще воспринимать и анализировать.
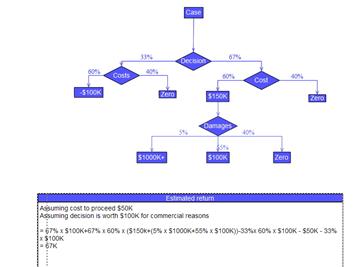 Типология деревьев
Деревья решений, используемые в Data Mining, бывают двух основных типов:
Типология деревьев
Деревья решений, используемые в Data Mining, бывают двух основных типов:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Динамическое программирование | Метод позволяет принять ряд последовательных решений (многошаговый процесс), обеспечивающих оптимальность развития в целом. Теоретическая основа – оптимальность развития Беллмана: на каждом этапе необходимо так распределять ресурсы, чтобы, начиная с этого этапа и до конца процессе распределения, доход был максимальным. Вся траектория движения разбивается на ряд участков. Процесс моделирования протекает в направлении, обратном ходу времени, от искомого (конечного) состояния к текущему, Сначала находится оптимальное решений для последнего, ближайшего к конечному состоянию, участка. Затем – решение оптимальное для отрезка, являющегося суммой последнего и предпоследнего участков и т.д.
Динамическое программирование в теории управления и теории вычислительных систем — способ решения сложных задач путём разбиения их на более простые подзадачи. Он применим к задачам с оптимальной подструктурой (англ.), выглядящим как набор перекрывающихся подзадач, сложность которых чуть меньше исходной. В этом случае время вычислений, по сравнению с «наивными» методами, можно значительно сократить.
Ключевая идея в динамическом программировании достаточно проста. Как правило, чтобы решить поставленную задачу, требуется решить отдельные части задачи (подзадачи), после чего объединить решения подзадач в одно общее решение. Часто многие из этих подзадач одинаковы. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений. Это особенно полезно в случаях, когда число повторяющихся подзадач экспоненциально велико.
Метод динамического программирования сверху — это простое запоминание результатов решения тех подзадач, которые могут повторно встретиться в дальнейшем. Динамическое программирование снизу включает в себя переформулирование сложной задачи в виде рекурсивной последовательности более простых подзадач.
Идея динамического программирования
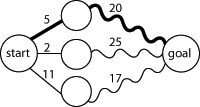
 Нахождение кратчайшего пути в графе из одной вершины в другую, используя оптимальную подструктуру; прямая линия обозначает простое ребро; волнистая линия обозначает кратчайший путь между вершинами, которые она соединяет (промежуточные вершины пути не показаны); жирной линией обозначен итоговый кратчайший путь.
Нахождение кратчайшего пути в графе из одной вершины в другую, используя оптимальную подструктуру; прямая линия обозначает простое ребро; волнистая линия обозначает кратчайший путь между вершинами, которые она соединяет (промежуточные вершины пути не показаны); жирной линией обозначен итоговый кратчайший путь.
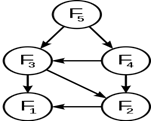
 Граф подзадач (ребро означает, что одна задача зависит от решения другой) для чисел Фибоначчи (граф — ациклический).
Оптимальная подструктура в динамическом программировании означает, что оптимальное решение подзадач меньшего размера может быть использовано для решения исходной задачи. К примеру, кратчайший путь в графе из одной вершины (обозначим s) в другую (обозначим t) может быть найден так: сначала считаем кратчайший путь из всех вершин, смежных с s, до t, а затем, учитывая веса ребер, которыми s соединена со смежными вершинами, выбираем лучший путь до t (через какую вершину лучше всего пойти). В общем случае мы можем решить задачу, в которой присутствует оптимальная подструктура, проделывая следующие три шага.
1. Разбиение задачи на подзадачи меньшего размера.
2. Нахождение оптимального решения подзадач рекурсивно, проделывая такой же трехшаговый алгоритм.
3. Использование полученного решения подзадач для конструирования решения исходной задачи.
Подзадачи решаются делением их на подзадачи ещё меньшего размера и т. д., пока не приходят к тривиальному случаю задачи, решаемой за константное время (ответ можно сказать сразу). К примеру, если нам нужно найти n!, то тривиальной задачей будет 1! = 1 (или 0! = 1).
Перекрывающиеся подзадачи в динамическом программировании означают подзадачи, которые используются для решения некоторого количества задач (не одной) большего размера (то есть мы несколько раз проделываем одно и то же). Ярким примером является вычисление последовательности Фибоначчи,
Граф подзадач (ребро означает, что одна задача зависит от решения другой) для чисел Фибоначчи (граф — ациклический).
Оптимальная подструктура в динамическом программировании означает, что оптимальное решение подзадач меньшего размера может быть использовано для решения исходной задачи. К примеру, кратчайший путь в графе из одной вершины (обозначим s) в другую (обозначим t) может быть найден так: сначала считаем кратчайший путь из всех вершин, смежных с s, до t, а затем, учитывая веса ребер, которыми s соединена со смежными вершинами, выбираем лучший путь до t (через какую вершину лучше всего пойти). В общем случае мы можем решить задачу, в которой присутствует оптимальная подструктура, проделывая следующие три шага.
1. Разбиение задачи на подзадачи меньшего размера.
2. Нахождение оптимального решения подзадач рекурсивно, проделывая такой же трехшаговый алгоритм.
3. Использование полученного решения подзадач для конструирования решения исходной задачи.
Подзадачи решаются делением их на подзадачи ещё меньшего размера и т. д., пока не приходят к тривиальному случаю задачи, решаемой за константное время (ответ можно сказать сразу). К примеру, если нам нужно найти n!, то тривиальной задачей будет 1! = 1 (или 0! = 1).
Перекрывающиеся подзадачи в динамическом программировании означают подзадачи, которые используются для решения некоторого количества задач (не одной) большего размера (то есть мы несколько раз проделываем одно и то же). Ярким примером является вычисление последовательности Фибоначчи, 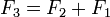 и и 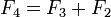 — даже в таком тривиальном случае вычисления всего двух чисел Фибоначчи мы уже посчитали — даже в таком тривиальном случае вычисления всего двух чисел Фибоначчи мы уже посчитали 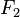 дважды. Если продолжать дальше и посчитать дважды. Если продолжать дальше и посчитать  , то , то 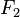 посчитается ещё два раза, так как для вычисления посчитается ещё два раза, так как для вычисления  будут нужны опять будут нужны опять 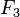 и и 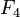 . Получается следующее: простой рекурсивный подход будет расходовать время на вычисление решение для задач, которые он уже решал.
Чтобы избежать такого хода событий мы будем сохранять решения подзадач, которые мы уже решали, и когда нам снова потребуется решение подзадачи, мы вместо того, чтобы вычислять его заново, просто достанем его из памяти. Этот подход называется кэширование. Можно проделывать и дальнейшие оптимизации — например, если мы точно уверены, что решение подзадачи нам больше не потребуется, можно выкинуть его из памяти, освободив её для других нужд, или если процессор простаивает и мы знаем, что решение некоторых, ещё не посчитанных подзадач, нам понадобится в дальнейшем, мы можем решить их заранее.
Подводя итоги вышесказанного можно сказать, что динамическое программирование пользуется следующими свойствами задачи:
· перекрывающиеся подзадачи;
· оптимальная подструктура;
· возможность запоминания решения часто встречающихся подзадач.
Динамическое программирование обычно придерживается двух подходов к решению задач:
· нисходящее динамическое программирование: задача разбивается на подзадачи меньшего размера, они решаются и затем комбинируются для решения исходной задачи. Используется запоминание для решений часто встречающихся подзадач.
· восходящее динамическое программирование: все подзадачи, которые впоследствии понадобятся для решения исходной задачи просчитываются заранее и затем используются для построения решения исходной задачи. Этот способ лучше нисходящего программирования в смысле размера необходимого стека и количества вызова функций, но иногда бывает нелегко заранее выяснить, решение каких подзадач нам потребуется в дальнейшем.
Языки программирования могут запоминать результат вызова функции с определенным набором аргументов (мемоизация), чтобы ускорить «вычисление по имени». В некоторых языках такая возможность встроена (например, Scheme, Common Lisp, Perl), а в некоторых требует дополнительных расширений (C++).
Известны сериальное динамическое программирование, включённое во все учебники по исследованию операций, и несериальное динамическое программирование (НСДП), которое в настоящее время слабо известно, хотя было открыто в 1960-х годах.
Обычное динамическое программирование является частным случаем несериального динамического программирования, когда граф взаимосвязей переменных — просто путь. НСДП, являясь естественным и общим методом для учета структуры задачи оптимизации, рассматривает множество ограничений и/или целевую функцию как рекурсивно вычислимую функцию. Это позволяет находить решение поэтапно, на каждом из этапов используя информацию, полученную на предыдущих этапах, причём эффективность этого алгоритма прямо зависит от структуры графа взаимосвязей переменных. Если этот граф достаточно разрежен, то объём вычислений на каждом этапе может сохраняться в разумных пределах.
Одним из основных свойств задач, решаемых с помощью динамического программирования, является аддитивность. Неаддитивные задачи решаются другими методами. Например, многие задачи по оптимизации инвестиций компании являются неаддитивными и решаются с помощью сравнения стоимости компании при проведении инвестиций и без них. . Получается следующее: простой рекурсивный подход будет расходовать время на вычисление решение для задач, которые он уже решал.
Чтобы избежать такого хода событий мы будем сохранять решения подзадач, которые мы уже решали, и когда нам снова потребуется решение подзадачи, мы вместо того, чтобы вычислять его заново, просто достанем его из памяти. Этот подход называется кэширование. Можно проделывать и дальнейшие оптимизации — например, если мы точно уверены, что решение подзадачи нам больше не потребуется, можно выкинуть его из памяти, освободив её для других нужд, или если процессор простаивает и мы знаем, что решение некоторых, ещё не посчитанных подзадач, нам понадобится в дальнейшем, мы можем решить их заранее.
Подводя итоги вышесказанного можно сказать, что динамическое программирование пользуется следующими свойствами задачи:
· перекрывающиеся подзадачи;
· оптимальная подструктура;
· возможность запоминания решения часто встречающихся подзадач.
Динамическое программирование обычно придерживается двух подходов к решению задач:
· нисходящее динамическое программирование: задача разбивается на подзадачи меньшего размера, они решаются и затем комбинируются для решения исходной задачи. Используется запоминание для решений часто встречающихся подзадач.
· восходящее динамическое программирование: все подзадачи, которые впоследствии понадобятся для решения исходной задачи просчитываются заранее и затем используются для построения решения исходной задачи. Этот способ лучше нисходящего программирования в смысле размера необходимого стека и количества вызова функций, но иногда бывает нелегко заранее выяснить, решение каких подзадач нам потребуется в дальнейшем.
Языки программирования могут запоминать результат вызова функции с определенным набором аргументов (мемоизация), чтобы ускорить «вычисление по имени». В некоторых языках такая возможность встроена (например, Scheme, Common Lisp, Perl), а в некоторых требует дополнительных расширений (C++).
Известны сериальное динамическое программирование, включённое во все учебники по исследованию операций, и несериальное динамическое программирование (НСДП), которое в настоящее время слабо известно, хотя было открыто в 1960-х годах.
Обычное динамическое программирование является частным случаем несериального динамического программирования, когда граф взаимосвязей переменных — просто путь. НСДП, являясь естественным и общим методом для учета структуры задачи оптимизации, рассматривает множество ограничений и/или целевую функцию как рекурсивно вычислимую функцию. Это позволяет находить решение поэтапно, на каждом из этапов используя информацию, полученную на предыдущих этапах, причём эффективность этого алгоритма прямо зависит от структуры графа взаимосвязей переменных. Если этот граф достаточно разрежен, то объём вычислений на каждом этапе может сохраняться в разумных пределах.
Одним из основных свойств задач, решаемых с помощью динамического программирования, является аддитивность. Неаддитивные задачи решаются другими методами. Например, многие задачи по оптимизации инвестиций компании являются неаддитивными и решаются с помощью сравнения стоимости компании при проведении инвестиций и без них.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дю Пон | Основан на исследовании коэффициента возврата на собственность путем ее разложения в виде произведения других, более простых и доступных для анализа показателей. Применим для анализа эффективности деятельности предприятий с позиции финансового менеджмента
Метод "Дюпон"
Иногда метод "Дюпон" называют методом Дюпона, что не имеет смысла, поскольку Эжен дю Пон де Немур умер в 1834 году, а метод был разработан группой специалистов компании "Дюпон" в двадцатые годы нашего столетия.
А. Описание метода "Дюпон"
Метод "Дюпон" основан на анализе соотношений, образующих коэффициент доходности акционерного капитала (Return on Equity, или ROE):
где: NI (Net Income) -- чистая прибыль, CE (Common Equity) -- акционерный капитал предприятия. Есть несколько версий метода, отличающихся степенью детализации. 1. Двухчленная версия
где: TA (Total Assets) -- суммарные активы предприятия Иначе можно записать: ROE = ROA * LR где: ROA (Return on Assets) -- доходность активов LR (Leverage Ratio) -- коэффициент финансового рычага 2. Трехчленная версия
где: NS (Net Sales) -- чистый (без учета НДС, налогов с оборота и налогов с продаж) объем реализации Иначе можно записать: ROE = NPM * AT * LR где: NPM (Net Profit Margin) -- рентабельность AT (Asset Turnover) -- оборачиваемость активов 3. Пятичленная версия
где: EBT (Earings before Taxes) -- прибыль до уплаты налогов EBIT (Earings before Interest and Taxes) -- прибыль до уплаты процентов и налогов Иначе можно записать: ROE = TB * IB * OM * AT * LR где: TB (Tax Burden) -- налоговое бремя IB (Interest Burden) -- бремя процентов OM (Operating Margin) -- операционная рентабельность Б. Простой пример анализа Рассмотрим коэффициенты метода "Дюпон" для некоторой вымышленной компании за этот и прошлый год (на практике стоит параллельно иметь перед собой заодно и баланс и счет прибылей и убытков, чтобы оперативно проверять по ним разного рода допущения, возникающие в процессе анализа):
Вот вариант толкования этой таблицы коэффициентов. В прошлом году компания не имела долгов (проверка: а что на балансе?), или, по крайней мере, не платила процентов (IB = 1). В этом году компания решила расширить операции (проверка: выросли ли объемы реализации? -- см. счет прибылей и убытков) за счет привлечения кредита (LR вырос с 2 до 3). В ходе расширени операций пришлось снизить отпускные цены и/или пойти на увеличение издержек (так или иначе, OM упала с 0.15 до 0.12, а AT -- с 1 до 0.8; прямо проверить это предположение по счету прибыей и убытков вряд ли получится -- нужна либо управленческая отчетность, либо человеческое раскрытие информации). Половина операционной прибыли ушла на уплату процентов (IB = 0.5). В результате доходность акционерного капитала снизилась более чем вдвое. В. Проблемы применения метода "Дюпон" в России Проблем с применением метода "Дюпон" в России всего три: 1. Совершенно непонятно, насколько велика описательная сила показателя суммарных активов: активы постоянно переоцениваются, при этом многие из них просто не имеют разумной исторической стоимости (в частности, активы, которыми наделялись приватизируемые предприятия, учитывались по придуманным Госкомценом "ценам"). 2. Совершенно понятно, что "чистая прибыль" в терминологии Министерства финансов России далеко не чистая, поскольку из нее выплачивается целый ряд реально понесенных издержек (премии сотрудникам, расходы по содержанию социальной сферы и т.п.) 3. В России не соблюдается принцип постоянства положений учетной политики, то есть, сменив учетную политику, компании не корректируют отчетность предыдущих лет в соответствии с вновь принятыми положениями, что может приводить к весьма забавным аберрациям при попытке провести анализ по методу "Дюпон".
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Задача распределения ресурсов | Применяется в случае наличия нескольких видов ресурсов, каждый вид ресурсов в определённом количестве и используется для n видов продукции. Метод позволяет определить, сколько и какого вида продукции следует произвести, чтобы такой выпуск был наилучшим для принятого критерия оптимальности Задача оптимального распределения ресурсов. Предприятие имеет свободных К млрд. руб. средств, которые оно может вложить в пять различных производственных программ. При этом прибыль от каждой из программ зависит от объема инвестиций. Эти зависимости fi известны и имеют следующий вид: f(х) = bx – ax2 и конкретно: f1(х1) = 0,18x1 – 0,05x12; f2(х2) = 0,16x2 – 0,04x22; f3(х3) = 0,14x3 – 0,02x32; f4(х4) = 0,12x4 – 0,02x42; f5(х5) = 0,1x5 – 0,01x52 млрд.руб. где х1, х2, х3, х4, х5 – инвестиции в программы, млрд.руб. Их общий объем равен К = 8,5 млрд.руб. Требуется найти неотрицательные объемы инвестиций х1, х2, х3, х4, х5 соответствующие наибольшей общей прибыли П = f1(х1) + f2(х2) + f3(х3) + f4(х4) + f5(х5). Решение: Возможны следующие варианты: 1) Все средства передаются первой программе; 2) Средства распределяются между первой и второй программами; 3) Средства распределяются между первой, второй и третьей программами; 4) Средства распределяются между первой, второй, третьей и четвертой программами; 5) Средства распределяются между первой, второй, третьей, четвертой и пятой программами. Рассмотрим все 5 вариантов. 1) К1 = х1 = 8,5 П1 = f1(х1) = 0,18 8,5 – 0,05 8,52 = – 2,08 млрд.руб. < 0, следов–но убыток. 2) К2 = х1 + х2 П2 = f1(х1) + f2(х2) 0,18 – 2 0,05х1 = 0,16 – 2 0,04х2 х1 + х2 = 8,5 0,1х1 – 0,08х2 = 0,02 х1 = 8,5 – х2 0,1 (8,5 – х2) – 0,08х2 = 0,02 0,85 – 0,1х2 – 0,08х2 = 0,02 0,85 – 0,18х2 = 0,02 0,18х2 = 0,83 х2 = 4,61 х1 = 8,5 – 4,61 = 3,89 П2 = 0,18 · 3,89 – 0,05 3,892 + 0,16 4,61 – 0,04 4,612 = 0,7 – 0,757 + 0,738 – 0,85 = – 0,169 млрд.руб. < 0, следов–но убыток. 3) К3 = х1 + х2 + х3 П3 = f1(х1) + f2(х2) + f3(х3) 0,18 – 0,1х1 = 0,16 – 0,08х2 0,16 – 0,08х2 = 0,14 – 2 · 0,02х3 х1 + х2 + х3 = 8,5 0,18 – 0,1х1 = 0,16 – 0,08х2 0,16 – 0,08х2 = 0,14 – 0,04х3 х1 + х2 + х3 = 8,5 0,1х1 – 0,08х2 = 0,18 – 0,16 · 50 0,08х2 – 0,04х3 = 0,16 – 0,14 х1 + х2 + х3 = 8,5 5х1 – 4х2 = 1 (1) 4х2 – 2х3 = 1 (2) х1 + х2 + х3 = 8,5 (3) Из 2 – го ур – ия: х3 = 2х2 – 0,5 5х1 – 4х2 = 1 х1 + х2 + 2х2 – 0,5 = 8,5 5х1 – 4х2 = 1 (1) х1 + 3х2 = 9 (2) Из 2 – го ур – ия: х1 = 9 – 3х2 5 (9 – 3х2) – 4х2 = 1 45 – 15х2 – 4х2 = 1 19х2 = 44 х1 = 9 – 3 · 2,316 = 2,052 х3 = 2 · 2,316 – 0,5 = 4,132 П3 = 0,18 · 2,052 – 0,05 · 2,0522 + 0,16 · 2,316 – 0,04 · 2,3162 + 0,14 · 4,132 – 0,02 · 4,1322 = 0,369 – 0,21 + 0,37 – 0,215 + 0,578 – 0,34 = 0,552 млрд.руб. 4) К4 = х1 + х2 + х3 + х4 П4 = f1(х1) + f2(х2) + f3(х3) + f4(х4) 0,18 – 0,1х1 = 0,16 – 0,08х2 0,16 – 0,08х2 = 0,14 – 0,04х3 0,14 – 0,04х3 = 0,12 – 0,04х4 х1 + х2 + х3 + х4 = 8,5 0,1х1 – 0,08х2 = 0,18 – 0,16 0,08х2 – 0,04х3 = 0,16 – 0,14 · 50 0,04х3 – 0,04х4 = 0,14 – 0,12 х1 + х2 + х3 + х4 = 8,5 5х1 – 4х2 = 1 (1) 4х2 – 2х3 = 1 (2) 2х3 – 2х4 = 1 (3) х1 + х2 + х3 +х4 = 8,5 (4) Из 3 – го ур – ия: х4 = х3 – 0,5 5х1 – 4х2 = 1 4х2 – 2х3 = 1 х1 + х2 + х3 + х3 – 0,5 = 8,5 5х1 – 4х2 = 1 (1) 4х2 – 2х3 = 1 (2) х1 + х2 + 2х3 = 9 (3) Из 2 – го ур – ия: х3 = 2х2 – 1 5х1 – 4х2 = 1 х1 + х2 + 2 (2х2 – 1) = 9 5х1 – 4х2 = 1 х1 + х2 + 4х2 – 2 = 9 5х1 – 4х2 = 1 (1) х1 + 5х2 = 11 (2) Из 2 – го ур – ия: х1 = 11 – 5х2 5 (11 – 5х2) – 4х2 = 1 55 – 25х2 – 4х2 =1 29х2 = 54 х2 = 1,862 х1 = 11 – 5 1,862 = 1,69 х3 = 2 · 1,862 – 1 = 2,724 х4 = 2,724 – 0,5 = 2,224 П4 = 0,18 1,69 – 0,05 1,692 + 0,16 1,862 – 0,04 1,8622 + 0,14 2,724 – 0,02·2,7242 + 0,12 2,224 – 0,02 2,2242 = 0,3 – 0,143 + 0,298 – 0,139 + 0,381 – 0,148 + 0,267 – 0,1 = 0,716 млрд.руб. 5) К5 = х1 + х2 + х3 + х4 +х5 П5 = f1(х1) + f2(х2) + f3(х3) + f4(х4) + f5(х5) 0,18 – 0,1х1 = 0,16 – 0,08х2 0,16 – 0,08х2 = 0,14 – 0,04х3 0,14 – 0,04х3 = 0,12 – 0,04х4 0,12 – 0,04х4 = 0,1 – 0,02х5 х1 + х2 + х3 + х4 + х5 = 8,5 0,1х1 – 0,08х2 = 0,18 – 0,16 0,08х2 – 0,04х3 = 0,16 – 0,14 0,04х3 – 0,04х4 = 0,14 – 0,12 0,04х4 – 0,02х5 = 0,12 – 0,1 х1 + х2 + х3 + х4 + х5 = 8,5 0,1х1 – 0,08х2 = 0,02 0,08х2 – 0,04х3 = 0,02 50 0,04х3 – 0,04х4 = 0,02 0,04х4 – 0,02х5 = 0,02 х1 + х2 + х3 + х4 + х5 = 8,5 5х1 – 4х2 = 1 (1) 4х2 – 2х3 = 1 (2) 2х3 – 2х4 = 1 (3) 2х4 – х5 = 1 (4) х1 + х2 + х3 +х4 + х5 = 8,5 (5) Из 4 – го ур – ия: х5 = 2х4 – 1 5х1 – 4х2 = 1 4х2 – 2х3 = 1 2х3 – 2х4 = 1 х1 + х2 + х3 +х4 + 2х4 – 1 = 8,5 5х1 – 4х2 = 1 (1) 4х2 – 2х3 = 1 (2) 2х3 – 2х4 = 1 (3) х1 + х2 + х3 + 3х4 = 9,5 (4) Из 3 – го ур – ия: х4 = х3 – 0,5 5х1 – 4х2 = 1 4х2 – 2х3 = 1 х1 + х2 + х3 + 3 (х3 – 0,5) = 9,5 5х1 – 4х2 = 1 4х2 – 2х3 = 1 х1 + х2 + 4х3 – 1,5 = 9,5 5х1 – 4х2 = 1 (1) 4х2 – 2х3 = 1 (2) х1 + х2 + 4х3 = 11 (3) Из 2 – го ур – ия: х3 = 2х2 – 0,5 5х1 – 4х2 = 1 х1 + х2 + 4 (2х2 – 0,5) = 11 5х1 – 4х2 = 1 х1 + х2 + 8х2 – 2 = 11 5х1 – 4х2 = 1 (1) х1 + 9х2 = 13 (2) Из 2 – го ур – ия: х1 = 13 – 9х2 5 (13 – 9х2) – 4х2 = 1 65 – 45х2 – 4х2 = 1 49х2 = 64 х2 = 1,306 х1 = 13 – 9 1,306 = 1,246 х3 = 2 1,306 – 0,5 = 2,112 х4 = 2,112 – 0,5 = 1,612 х5 = 2 · 1,612 – 1 = 2,224 П5 = 0,18 1,246 – 0,05 1,2462 + 0,16 1,306 – 0,04 1,3062 + 0,14 2,112 – 0,02 2,1122 + 0,12 1,612 – 0,02 1,6122 + 0,1 2,224 – 0,01 2,2242 = 0,224 – 0,078 + 0,209 – 0,068 + 0,296 – 0,089 + 0,193 – 0,052 + 0,222 – 0,049 = 0,808 млрд.руб. Ответ: Максимальное значение прибыли П5 = 0,808 млрд. руб. Распределение инвестиций: х1 = 1,246 млрд. руб. х2 = 1,306 млрд. руб. х3 = 2,112 млрд. руб. х4 = 1,612 млрд. руб. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Затраты-выпуск | Проблема (цель, задача) рассматривается с точки зрения затрат, результатов и ограниченных ресурсов. Варианты решения оцениваются по этим показателям
Модели "затраты – выпуск" относят к моделям структурно-балансового типа. При построении микромодели (модели предприятия) в качестве отраслей рассматриваются технологические блоки экономической системы (предприятия) и моделируются процессы, связанные с движением ресурсов между блоками этой системы. Структура производственного процесса в каждом технологическом блоке представляется определенным вектором структурных коэффициентов, в котором отражается характер количественных связей между затратами и результатами (выпуском продукции данного конкретного блока). Связи представляют собой статистические данные экономики за конкретный период (год или ряд лет) в стоимостном или в натуральном выражении.
С математической точки зрения модель представляет собой систему уравнений, выражающую балансы между затратами и выпуском продукции. Каждое уравнение системы выражает требование баланса между произведенным количеством продукции и совокупной потребностью в этой продукции в каждом блоке предприятия
Иными словами, балансовые соотношения (система уравнений) отражают «приход» и «расход» каждой компоненты материально-вещественных потоков в блоках, описывающих предприятие..[ Гранберг А.Г., Математические модели социалистической экономики, М.: Экономика, 1978.- 351 с.].
Под исходными данными понимается планируемый объем реализации продукции, а под выходными, — четко сбалансированная структура всего комплекса затрат, необходимых для того, чтобы этот объем продукции произвести. Параметрами (ключевыми характеристиками) модели являются коэффициенты затрат на производство продукции. Решение системы уравнений позволяет определить, какими должны быть выпуск и затраты в каждой отрасли, чтобы обеспечить производство конечного продукта заданного объема и структуры.
Модели «затраты-выпуск» служат двум целям: статистической и аналитической [Гранберг А.Г. Математические модели социалистической экономики. – М.: Экономика, 1978. – 351 с. ]. Они обеспечивают детальный анализ процесса производства и использования товаров и услуг, а также доходов, образующихся в результате такого производства, и создают основу для проверки согласованности статистических данных. Аналитическая функция состоит в том, что они позволяют моделировать экономическую ситуацию на основе коэффициентов прямых и полных затрат.
В классическом виде модель межотраслевого баланса «затраты-выпуск» имеет вид:
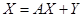 или или  , ,  .
где .
где  – вектор-столбец валовых выпусков, – вектор-столбец валовых выпусков, 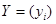 – вектор-столбец конечной продукции, – вектор-столбец конечной продукции, 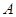 – матрица коэффициентов прямых затрат, – матрица коэффициентов прямых затрат,  – единичная матрица.
При необходимости модель может быть дополнена различными ограничениями, позволяющими уточнить описание условий функционирования предприятия.
На базе модели з-в выделяют такие типовые задачи прогнозирования: [Белозеров В. К., аспирант Вологодский научно-координационный центр ЦЭМИ РАН.]
- Определение сбалансированных выпусков продукции, обеспечивающих задаваемые варианты конечного спроса.
- Определение объемов конечного спроса исходя из заданных выпусков.
- Расчеты сбалансированных объемов выпуска и конечного спроса со смешанным составом неизвестных.
- Проведение структурного анализа взаимосвязей выпусков, производственных ресурсов и конечного спроса
- Модель межотраслевых зависимостей цен и добавленной стоимости
- Межотраслевые зависимости конечного спроса и добавленной стоимости.
Развитием статической межотраслевой модели являются динамические модели "затраты – выпуск". Они позволяют отражать взаимосвязи между блоками экономической системы на каждом интервале времени. При этом из состава конечной продукции выделяются производственные капитальные вложения, исследуется их структура и влияние на рост объёма производства.
В основе построения модели в виде динамической системы уравнений лежит математическая зависимость между величиной капитальных вложений и приростом продукции. Решение системы, как и в случае статической модели, приводит к определению уровней производства, но в динамическом варианте в отличие от статистического эти искомые уровни зависят от объёмов производства в предшествующих периодах.
Таким образом, решение динамической системы линейных уравнений позволяет определить выпуск продукции в последующем периоде в зависимости от уровня, достигнутого в предыдущем периоде. Связь между периодами устанавливается через коэффициенты вложений, характеризующие фондоёмкость единицы прироста продукции.
В отличие от уравнений статической модели «з-в», где конечный продукт каждой отрасли представлен одним слагаемым, здесь он распадается на два — фонд накопления и фонд непроизводственного потребления. Модель показывает, что для управления процессом решающее значение имеет соотношение между фондом накопления и фондом потребления конечной продукции.
Экономистами разрабатываются разные типы динамических моделей затраты-выпуск, примерами таких моделей могут быть:
- модели с обратной рекурсией, в которых балансы производства и распределения продукции за последний год планового периода сочетаются с уравнениями потребности в капитальных вложениях за весь плановый период.
- модели поэтапного расчета объемов производства продукции и капитальных вложений для каждого года планового периода.
- модели с явным учетом лага капитальных вложений, в которых показана прямая и обратная их связь во времени с показателями производства продукции и д.р.
Модели, которые не только описывают взаимосвязи параметров внутреннего состояния производственной системы, но и дают возможность находить оптимальные варианты функционирования предприятия, образуют класс оптимизационных моделей производства [Волков, В.Н. Информационные технологии и моделирование в организационном проектировании [Текст] / Информационные технологии и математическое моделирование: Материалы III Всероссийской научно-практической конференции (11-12 декабря 2004г.). Т1. - Томск: изд-во Том. ун-та, 2004. - 188с. - С.54-56.]. Оптимизационные модели предполагают построение целевой функции, задание критерия оптимальности (экстремума целевой функции, например, максимума прибыли, минимума затрат и т.п.) и ограничений, описывающих важнейшие условия функционирования и взаимосвязи параметров предприятия. В зависимости от вида функций, участвующих в формировании цели и ограничений, различают линейные и нелинейные, целочисленные и смешанные модели [4].
С учетом того, что эффективные методы решения задач математического программирования имеются лишь для статических задач линейного и выпуклого программирования, соответствующие модели функционирования предприятий, как правило, являются весьма упрощенными и обычно применяются для решения частных вопросов, таких, например, как оптимальное распределение ресурсов и/или использования производственных мощностей, оптимальный выбор технологических способов производства заданного ассортимента продукции, определение оптимальной производственной программы и т.п. [[Кобринский Н.Е., Майминас Е.З., Смирнов А.Д. Введение в экономическую кибернетику: Учебное пособие - М.: «Экономика», 1975. – 343 с.]Вагнер, исследоване операций].
Структура оптимизационной модели состоит из переменных (управляемых и неуправляемых), соотношений, описывающих важнейшие условия функционирования объекта, (системы ограничений) и целевой функции. В общем виде оптимизационная модель выглядит следующим образом
Целевая функция: – единичная матрица.
При необходимости модель может быть дополнена различными ограничениями, позволяющими уточнить описание условий функционирования предприятия.
На базе модели з-в выделяют такие типовые задачи прогнозирования: [Белозеров В. К., аспирант Вологодский научно-координационный центр ЦЭМИ РАН.]
- Определение сбалансированных выпусков продукции, обеспечивающих задаваемые варианты конечного спроса.
- Определение объемов конечного спроса исходя из заданных выпусков.
- Расчеты сбалансированных объемов выпуска и конечного спроса со смешанным составом неизвестных.
- Проведение структурного анализа взаимосвязей выпусков, производственных ресурсов и конечного спроса
- Модель межотраслевых зависимостей цен и добавленной стоимости
- Межотраслевые зависимости конечного спроса и добавленной стоимости.
Развитием статической межотраслевой модели являются динамические модели "затраты – выпуск". Они позволяют отражать взаимосвязи между блоками экономической системы на каждом интервале времени. При этом из состава конечной продукции выделяются производственные капитальные вложения, исследуется их структура и влияние на рост объёма производства.
В основе построения модели в виде динамической системы уравнений лежит математическая зависимость между величиной капитальных вложений и приростом продукции. Решение системы, как и в случае статической модели, приводит к определению уровней производства, но в динамическом варианте в отличие от статистического эти искомые уровни зависят от объёмов производства в предшествующих периодах.
Таким образом, решение динамической системы линейных уравнений позволяет определить выпуск продукции в последующем периоде в зависимости от уровня, достигнутого в предыдущем периоде. Связь между периодами устанавливается через коэффициенты вложений, характеризующие фондоёмкость единицы прироста продукции.
В отличие от уравнений статической модели «з-в», где конечный продукт каждой отрасли представлен одним слагаемым, здесь он распадается на два — фонд накопления и фонд непроизводственного потребления. Модель показывает, что для управления процессом решающее значение имеет соотношение между фондом накопления и фондом потребления конечной продукции.
Экономистами разрабатываются разные типы динамических моделей затраты-выпуск, примерами таких моделей могут быть:
- модели с обратной рекурсией, в которых балансы производства и распределения продукции за последний год планового периода сочетаются с уравнениями потребности в капитальных вложениях за весь плановый период.
- модели поэтапного расчета объемов производства продукции и капитальных вложений для каждого года планового периода.
- модели с явным учетом лага капитальных вложений, в которых показана прямая и обратная их связь во времени с показателями производства продукции и д.р.
Модели, которые не только описывают взаимосвязи параметров внутреннего состояния производственной системы, но и дают возможность находить оптимальные варианты функционирования предприятия, образуют класс оптимизационных моделей производства [Волков, В.Н. Информационные технологии и моделирование в организационном проектировании [Текст] / Информационные технологии и математическое моделирование: Материалы III Всероссийской научно-практической конференции (11-12 декабря 2004г.). Т1. - Томск: изд-во Том. ун-та, 2004. - 188с. - С.54-56.]. Оптимизационные модели предполагают построение целевой функции, задание критерия оптимальности (экстремума целевой функции, например, максимума прибыли, минимума затрат и т.п.) и ограничений, описывающих важнейшие условия функционирования и взаимосвязи параметров предприятия. В зависимости от вида функций, участвующих в формировании цели и ограничений, различают линейные и нелинейные, целочисленные и смешанные модели [4].
С учетом того, что эффективные методы решения задач математического программирования имеются лишь для статических задач линейного и выпуклого программирования, соответствующие модели функционирования предприятий, как правило, являются весьма упрощенными и обычно применяются для решения частных вопросов, таких, например, как оптимальное распределение ресурсов и/или использования производственных мощностей, оптимальный выбор технологических способов производства заданного ассортимента продукции, определение оптимальной производственной программы и т.п. [[Кобринский Н.Е., Майминас Е.З., Смирнов А.Д. Введение в экономическую кибернетику: Учебное пособие - М.: «Экономика», 1975. – 343 с.]Вагнер, исследоване операций].
Структура оптимизационной модели состоит из переменных (управляемых и неуправляемых), соотношений, описывающих важнейшие условия функционирования объекта, (системы ограничений) и целевой функции. В общем виде оптимизационная модель выглядит следующим образом
Целевая функция:
 при следующих ограничениях:
при следующих ограничениях:
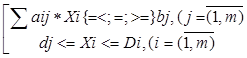 (где: E - целевая функция; Ci- коэффициенты при переменных в целевой функции; Xi - переменные задачи; bj - правые части ограничений; аij - коэффициенты при переменных в ограничениях; di - минимально возможные значения переменных; Di - максимально возможные значения переменных).
Исходными данными для таких моделей являются основные показатели, описывающие функционирование предприятия: объемы ресурсов, производственные мощности и т.д. В качестве коэффициентов при переменных в целевой функции могут выступать нормативные коэффициенты показателей качества работы предприятия, например прибыль, затраты и т.д.
Зависимость межу переменными в целевой функции и ограничения может носить как линейный, так и нелинейный характер.
Соответственно различают линейные и нелинейные оптимизационные модели.
Наибольшее распространение в практике управления экономическими объектами имеют линейные оптимизационные модели. Математическая постановка задачи линейной оптимизации хорошо изучена и не представляет научных проблем. Основанием этому служат два основных момента.
Во-первых, аппарат линейных функций удобен и прост для понимания. Канторович в своей Нобелевской речи говорил, что несмотря на универсальность и хорошую точность, модель линейного программирования использует весьма элементарный инструментарий линейной алгебры и понимание и овладение ею дает возможность творческого, а не шаблонного использования предлагаемых моделью средств анализа. Во-вторых, для линейных моделей разработаны высокоэффективные методы нахождения оптимальных значений переменных.
Наиболее распространенной моделью является классическая линейная модель производства, которая позволяет представить взаимозаменяемость и комбинирование фиксированных технологических способов, считающихся основными, в некоторых пределах, обозначенных ресурсами и плановыми ограничениями. Здесь каждый технологический способ (в том числе эффективный) может быть представлен в виде линейной комбинации с положительными коэффициентами так называемых базисных производственных способов
Основное применение линейные оптимизационные модели получили при построении следующих основных классов задач: формирование производственной программы; распределение ресурсов; управление запасами; задача ремонта и замены оборудования и т.п.. Применение линейных оптимизационных методов в экономике и построенные на их базе модели предприятий и модели планирования производства широко описаны и расклассифицированы в литературе (см., например, [19] [10. Португал В. М., Семенов А. И. Модели планирования на предприятии.— М.: Наука, 1978.— 272с.; Первин Ю. А., Португал В. М., Семенов А. И. Планирование мелкосерийного производства в АСУП. М., «Наука, 1973. 22. Португал В. М., Марголин А. Л. Автоматизация оперативного управления машиностроительным предприятием. М., «Статистика», 1976.;Багриновский К.А. Экономико-математические методы и модели (микроэкономика): учеб. пособие / К.А. Багриновский, В.М. Матюшок. – Изд. 2-е перераб. и доп. – М.: Изд-во РУДН, 2006. – 220 с.:],
Критерий решения задачи и управляющие переменные позволяют по-разному моделировать производство (составлять разные модели на базе одного и того же предприятия). Но, однако, чем детальнее описание предприятия, тем сложнее постановка задачи. Соответственно, тем сложнее модель и методы ее решения.
Кроме того, линейные оптимизационные модели искажают описание самого предприятия. Это связано с тем, что ограничения модели позволяют выделять лишь отдельные стороны сложной системы, которой является предприятие, а процессы, происходящие на предприятии, к тому же, далеко не всегда имеют линейный характер. Это приводит к вынужденному упрощению действительности и, соответственно полученные рекомендации по поводу оптимальных управляющих решений на деле могут оказаться неточными (достоверность полученных из модели выводов может быть подвержена сомнению).
Если в ходе производственного процесса становятся возможными значительные изменения интенсивностей технологических способов, то предположение о пропорциональности затрат ресурсов и результатов хозяйственной деятельности является, вообще говоря, неверным. Тем самым нарушается одна из важнейших предпосылок построения линейной модели и становится необходимым использовать более сложные, нелинейные оптимизационные модели производства. Наиболее естественным обобщением таких моделей является выпуклая модель производства [Данилов Н.Н. "Курс математической экономики" Высшая школа, 2006. - 407 стр.]. В ней множество допустимых интенсивностей производства описано при помощи вогнутых функций, а для выбора наилучшего решения задается выпуклая вверх функция аргументов, которая обычно имеет смысл выпуска товарной продукции.
В оптимизационных задачах отдельно можно выделить модели календарного планирования.
Критерии оптимальности в этих задачах - минимизация затрат времени на выполнение всех работ, минимизация общего запаздывания, выполнение работ против норматива, минимизация потерь от запаздывания и т.п. [19 Португал с. стр 26]. К ним относятся модели планировании загрузки участка однотипных взаимозамещаемых станков, модели задачи теории расписаний, модели задач трех станков и д.р. В постановке этих задач обычно отсутствует такой фактор, как технология изготовления изделий, поэтому задача приводится к относительно нетрудоемким вычислительным схемам линейного программирования.
Преимущественно они решают задачи частного характера и разрабатываются для организации производства на каждом участке предприятия.
(где: E - целевая функция; Ci- коэффициенты при переменных в целевой функции; Xi - переменные задачи; bj - правые части ограничений; аij - коэффициенты при переменных в ограничениях; di - минимально возможные значения переменных; Di - максимально возможные значения переменных).
Исходными данными для таких моделей являются основные показатели, описывающие функционирование предприятия: объемы ресурсов, производственные мощности и т.д. В качестве коэффициентов при переменных в целевой функции могут выступать нормативные коэффициенты показателей качества работы предприятия, например прибыль, затраты и т.д.
Зависимость межу переменными в целевой функции и ограничения может носить как линейный, так и нелинейный характер.
Соответственно различают линейные и нелинейные оптимизационные модели.
Наибольшее распространение в практике управления экономическими объектами имеют линейные оптимизационные модели. Математическая постановка задачи линейной оптимизации хорошо изучена и не представляет научных проблем. Основанием этому служат два основных момента.
Во-первых, аппарат линейных функций удобен и прост для понимания. Канторович в своей Нобелевской речи говорил, что несмотря на универсальность и хорошую точность, модель линейного программирования использует весьма элементарный инструментарий линейной алгебры и понимание и овладение ею дает возможность творческого, а не шаблонного использования предлагаемых моделью средств анализа. Во-вторых, для линейных моделей разработаны высокоэффективные методы нахождения оптимальных значений переменных.
Наиболее распространенной моделью является классическая линейная модель производства, которая позволяет представить взаимозаменяемость и комбинирование фиксированных технологических способов, считающихся основными, в некоторых пределах, обозначенных ресурсами и плановыми ограничениями. Здесь каждый технологический способ (в том числе эффективный) может быть представлен в виде линейной комбинации с положительными коэффициентами так называемых базисных производственных способов
Основное применение линейные оптимизационные модели получили при построении следующих основных классов задач: формирование производственной программы; распределение ресурсов; управление запасами; задача ремонта и замены оборудования и т.п.. Применение линейных оптимизационных методов в экономике и построенные на их базе модели предприятий и модели планирования производства широко описаны и расклассифицированы в литературе (см., например, [19] [10. Португал В. М., Семенов А. И. Модели планирования на предприятии.— М.: Наука, 1978.— 272с.; Первин Ю. А., Португал В. М., Семенов А. И. Планирование мелкосерийного производства в АСУП. М., «Наука, 1973. 22. Португал В. М., Марголин А. Л. Автоматизация оперативного управления машиностроительным предприятием. М., «Статистика», 1976.;Багриновский К.А. Экономико-математические методы и модели (микроэкономика): учеб. пособие / К.А. Багриновский, В.М. Матюшок. – Изд. 2-е перераб. и доп. – М.: Изд-во РУДН, 2006. – 220 с.:],
Критерий решения задачи и управляющие переменные позволяют по-разному моделировать производство (составлять разные модели на базе одного и того же предприятия). Но, однако, чем детальнее описание предприятия, тем сложнее постановка задачи. Соответственно, тем сложнее модель и методы ее решения.
Кроме того, линейные оптимизационные модели искажают описание самого предприятия. Это связано с тем, что ограничения модели позволяют выделять лишь отдельные стороны сложной системы, которой является предприятие, а процессы, происходящие на предприятии, к тому же, далеко не всегда имеют линейный характер. Это приводит к вынужденному упрощению действительности и, соответственно полученные рекомендации по поводу оптимальных управляющих решений на деле могут оказаться неточными (достоверность полученных из модели выводов может быть подвержена сомнению).
Если в ходе производственного процесса становятся возможными значительные изменения интенсивностей технологических способов, то предположение о пропорциональности затрат ресурсов и результатов хозяйственной деятельности является, вообще говоря, неверным. Тем самым нарушается одна из важнейших предпосылок построения линейной модели и становится необходимым использовать более сложные, нелинейные оптимизационные модели производства. Наиболее естественным обобщением таких моделей является выпуклая модель производства [Данилов Н.Н. "Курс математической экономики" Высшая школа, 2006. - 407 стр.]. В ней множество допустимых интенсивностей производства описано при помощи вогнутых функций, а для выбора наилучшего решения задается выпуклая вверх функция аргументов, которая обычно имеет смысл выпуска товарной продукции.
В оптимизационных задачах отдельно можно выделить модели календарного планирования.
Критерии оптимальности в этих задачах - минимизация затрат времени на выполнение всех работ, минимизация общего запаздывания, выполнение работ против норматива, минимизация потерь от запаздывания и т.п. [19 Португал с. стр 26]. К ним относятся модели планировании загрузки участка однотипных взаимозамещаемых станков, модели задачи теории расписаний, модели задач трех станков и д.р. В постановке этих задач обычно отсутствует такой фактор, как технология изготовления изделий, поэтому задача приводится к относительно нетрудоемким вычислительным схемам линейного программирования.
Преимущественно они решают задачи частного характера и разрабатываются для организации производства на каждом участке предприятия.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Интерполяция | По некоторым значениям некоторой функции (выпуск-ресурсы, число занятых – годы и т.д.) прогнозируются неизвестные до этого значения внутри интервала заданных функциональных значений
Примеры интерполяции функций
При кажущейся простоте интерполяционных формул их реализация в виде программных блоков довольно громоздка. Приведем примеры простейших вариантов программных блоков, описывающих функции интерполяции рассмотренными методами. В наших примерах x, y – векторы табличных значений аргумента и функции (узлы); xf – значение аргумента, при котором требуется вычислить значение функции.
1. Формула линейной интерполяции применяется для той пары узлов, между которыми находится значение аргумента, поэтому в представленном блоке в цикле перебираются узлы с целью определить нужную пару:
 2. Непосредственно в математических символах записать интерполяционную формулу Лагранжа проблематично из-за сложности вычисления произведений (в обоих случаях исключается один сомножитель), поэтому предлагается такой программный блок::
2. Непосредственно в математических символах записать интерполяционную формулу Лагранжа проблематично из-за сложности вычисления произведений (в обоих случаях исключается один сомножитель), поэтому предлагается такой программный блок::
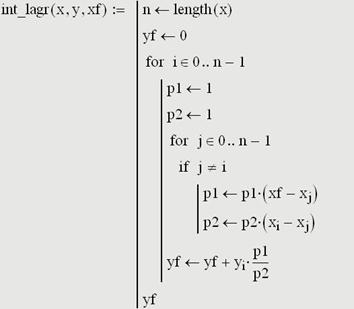 3. Mathcad имеет встроенную функцию linterp(vx, vy, x), возвращающую значение функции в точке x, вычисленное при линейной интерполяции данных с точками, координаты которых хранятся в векторах
3. Mathcad имеет встроенную функцию linterp(vx, vy, x), возвращающую значение функции в точке x, вычисленное при линейной интерполяции данных с точками, координаты которых хранятся в векторах
Дата добавления: 2014-01-07; Просмотров: 1768; Нарушение авторских прав?; Мы поможем в написании вашей работы! |
Генерация страницы за: 0.011 сек.
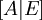 , после чего
, после чего 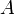 приводится к виду единичной матрицы методом Гаусса—Жордана; в результате на месте изначальной единичной матрицы справа оказывается обратная к исходной матрица:
приводится к виду единичной матрицы методом Гаусса—Жордана; в результате на месте изначальной единичной матрицы справа оказывается обратная к исходной матрица: 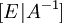 );
); 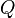 , помещаем его в корень.
, помещаем его в корень.  :
: