Математическое описание электромагнитных волн. Волновые уравнения

Распространение электромагнитного поля в пространстве – это волновой процесс, описание которого можно получить из уравнений Максвелла. Уравнения Максвелла описывают свойства электромагнитных волн в наиболее общем случае, но их непосредственное использование не всегда удобно. Поэтому для случая линейных и однородных сред можно получить более простые волновые уравнения, из которых следуют все законы геометрической оптики.

В оптике часто рассматривают изменение электрического и магнитного полей независимо друг от друга, и тогда векторный характер поля не является существенным, а электромагнитное поле можно рассматривать и описывать как скалярное. Скалярная теория значительно проще векторной, и вместе с тем дает возможность достаточно глубоко анализировать распространение световых пучков и процессы образования изображения в оптических системах. В геометрической оптике скалярная теория широко используется именно благодаря тому, что электрическое и магнитное поля в этом случае могут быть описаны независимо друг от друга, а волновые уравнения одинаковы для векторного и скалярного полей.

Рассмотрим вывод волновых уравнений непосредственно из уравнений Максвелла. Для этого проведем преобразования уравнений Максвелла для однородной, нейтральной 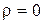(отсутствуют свободные заряды), непроводящей 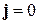(отсутствуют токи проводимости) среды. Используя символический дифференциальный оператор Гамильтона 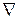(читается "набла"), перепишем их в виде:

, , ,

, , .

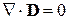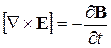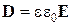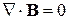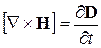В декартовой системе координат векторный оператор Гамильтона имеет вид , где - единичные векторы по осям .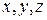

Произведение 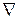на скаляр, например, 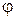- есть вектор, называемый "градиент 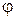", который характеризует изменения, испытываемые скаляром при изменении координат : .

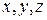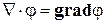Скалярное произведение символического вектора 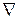на произвольный вектор 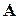есть дивергенция вектора : .

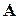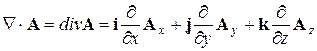Векторное произведение символического вектора 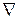на произвольный вектор 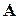есть ротор вектора 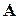: 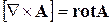, который может быть представлен в форме символического определителя , где -единичные векторы по осям 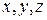, а 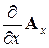- частная производная от по .

Возьмем уравнение для ротора электрического поля, определяемого через производную по времени от магнитной индукции:

.

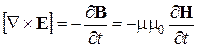Осуществив серию математических преобразований получим волновое уравнение для электрической составляющей поля:

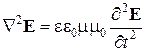
или

.

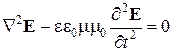Воспользовавшись тем, что 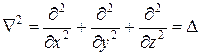- оператор Лапласа, волновое уравнение запишем в виде:

.

Воспользовавшись выражением для скорости распространения электромагнитной волны в веществе

,

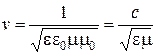где 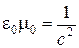, окончательно получим

.

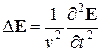Рассуждая аналогичным образом, можно получить волновое уравнение для магнитной составляющей поля:

.

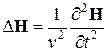Последние выражения получены для электромагнитных волн, распространяющихся в веществе. Для вакуума же они будут иметь вид:

,

.

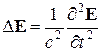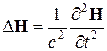Из уравнений Максвелла следует, что каждая из составляющих вектора подчиняется абсолютно одному и тому же скалярному уравнению. Поэтому, если требуется знать изменение только какой-нибудь одной из составляющих вектора , мы можем рассматривать векторное поле как скалярное. Перед тем, как окончательно перейти к скалярной теории, следует заметить, что составляющие вектора не являются независимыми функциями, что вытекает из условия . Поэтому, хотя скалярные волновые уравнения являются следствием уравнений Максвелла, обратно перейти от них к уравнениям Максвелла нельзя.

Пусть скалярная величина 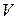– это любая из составляющих электрического вектора: (). Иными словами, это возмущение поля в какой-то точке пространства в какой-то момент времени 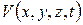. Тогда можно записать волновое уравнение в общем виде:

,

а для одной оси координат:

.

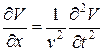Дата добавления: 2014-01-07