Решение системы уравнений методом итерации

Наиболее распространенным приемом аналитического решения систем линейных уравнений является алгоритм последовательного исключения неизвестных. Этот метод носит название метода Гаусса. При большом числе неизвестных линейной системы схема метода Гаусса, дающая точное решение, становится весьма сложной. В этих условиях для нахождения корней системы иногда удобнее пользоваться приближенными численными методами. Изложим здесь один из этих методов — метод итерации.

Пусть дана линейная система (1), запишем ее в виде матричного уравнения

Ах = b.

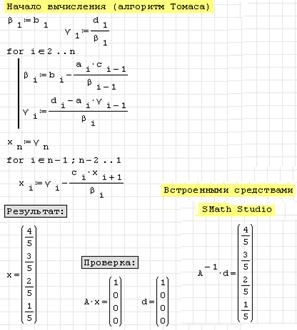
Рис. 2

Предполагая, что диагональные коэффициенты

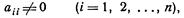
решим первое уравнение системы (1) относительно x₁, второе — относительно х₂ и т. д. Тогда получим эквивалентную систему

где

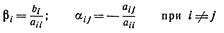
и α_ij=0 при i = j (i,j =1, 2, …, n).

Введя матрицы

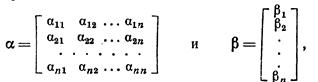
систему (5) можно записать в матричной форме

x = β + αx. (14)

Систему (13) будем решать методом последовательных приближений. За нулевое приближение принимаем, например, столбец свободных членов х⁽⁰⁾ = β.

Далее последовательно строим матрицы-столбцы

х⁽¹⁾ = β + αх⁽⁰⁾

(первое приближение),

х⁽²⁾ = β + αх⁽¹⁾

(второе приближение) и т. д.

Вообще говоря, любое (k+1)-е приближение вычисляют по формуле

х^(k+1) = β + αх^(k) (k = 0, 1, 2,...). (15)

Если последовательность приближений х⁽⁰⁾, х⁽¹⁾,…, х^(k),… имеет предел

то этот предел является решением системы (13). В самом деле, переходя к пределу в равенстве (15), будем иметь:

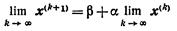
или

х = β + αх,

т. е. предельный вектор х является решением системы (13), а следовательно, и системы (1).

Напишем формулы приближений в развернутом виде:

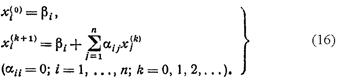
Метод последовательных приближений, определяемых формулой (15) или (16), носит название метода итерации. Процесс итерации (15) хорошо сходится.

Число приближений, необходимых для получения корней системы (1) с заданной точностью, невелико, если элементы матрицы малы по абсолютной величине. Иными словами, для успешного применения процесса итерации модули диагональных коэффициентов системы (1) должны быть велики по сравнению с модулями недиагональных коэффициентов этой системы (свободные члены при этом роли не играют).

Задание. При выполнении лабораторной работы необходимо изучить алгоритм метода итерации, разработать программу для его реализации и решить примеры в соответствии со своим вариантом.

Дата добавления: 2014-01-07