Программирование численного метода Ньютона

Метод Ньютона является наиболее распространенным методом решения систем нелинейных уравнений. Он обеспечивает более быструю сходимость по сравнению с методом простых итераций. В основе метода Ньютона лежит идея линеаризации всех нелинейных уравнений системы (17). Геометрически метод Ньютона эквивалентен замене небольшой дуги кривой y=f(x) касательной, проведенной в некоторой точке кривой. В самом деле, положим для определенности, что f" (х) > 0 при а≤ x ≤ b и f(b) > 0 (рис. 5).

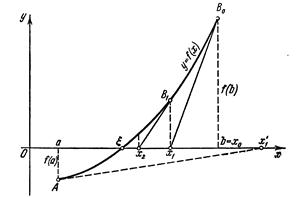
Рис. 5

Выберем, например, х₀ = b, для которого f(x₀) f" (x₀) > 0. Проведем касательную к кривой y=f(x) в точке B₀[х₀, f(x₀)].

В качестве первого приближения х₁ корня ξ возьмем абсциссу точки пересечения этой касательной с осью 0х. Через точку B₁[x₁,f(x₁)] снова проведем касательную, абсцисса точки пересечения которой даст нам второе приближение х₂ корня ξ и т. д. (рис. 5). Очевидно, что уравнение касательной в точке В_n [х_n,f(х_n)] (n = 0, 1,2,...) есть

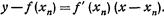
Полагая y = 0, x=x_n+1, получаем следующее приближение корня

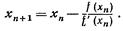
Рис. 6

Заметим, что если в нашем случае положить x₀ = a и, следовательно, f(x₀)f" (х₀) < 0, то, проведя касательную к кривой у = f(х) в точке А[а, f(a)], мы получили бы точку x₁ (рис. 5), лежащую вне отрезка [a,b]. То есть при этом выборе начального значения метод Ньютона оказывается непрактичным. Таким образом, в данном случае «хорошим» начальным приближением х₀ является то, для которого выполнено неравенство f(x₀)f" (х₀) > 0.

Пример реализации алгоритма решения систем нелинейных уравнений методом Ньютона в SMath Studio представлен на рис. 6.

Пользователь задаёт уравнения системы (допускается ввод как одного уравнения, так и нескольких) и начальные приближения. Расчёт вычисления корней системы нелинейных уравнений производится с использованием матрицы Якоби. Алгоритм позволяет также задать точность, с которой необходимо получить корни.

В результате работы программа демонстрирует полученные корни и проводит их проверку путём подстановки полученных корней в начальную систему уравнений. Для анализа работы алгоритма в примере выводится количество итераций (шагов в цикле), за которое удалось достигнуть результата.

Задание. При выполнении лабораторной работы необходимо изучить программную реализацию метода Ньютона (рис. 6), ввести программу в компьютер и решить примеры в соответствии со своим вариантом.

Дата добавления: 2014-01-07