Частные производные. Для определения понятия частной производной рассмотрим вначале так называемые частные приращения функции в точке

Лекция 12

Для определения понятия частной производной рассмотрим вначале так называемые частные приращения функции 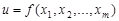в точке 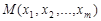, принадлежащей области определения функции. Зафиксируем все аргументы, кроме первого, а первому аргументу придадим произвольное приращение 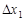такое, что точка с 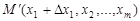находится в области определения функции. Разность значений функции в точках 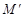и называется частным приращением функции в точке , соответствующим приращению 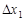аргумента 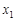и обозначается 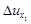. Итак

.

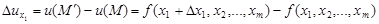Аналогично определяются частные приращения функции, соответствующие приращениям других аргументов. Зафиксируем все аргументы кроме -ого, а -ому придадим приращение 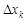. Тогда частичное приращение функции 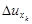— это разность значений функции в точках 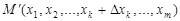и 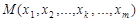, то есть

.

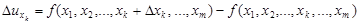Например, для функции двух переменных 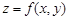частичные приращения по 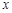и определяются формулами:

,

.

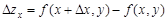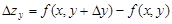Определение. Если существует предел отношения частного приращения 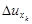функции 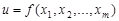в точке 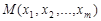к соответствующему приращению 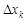аргумента 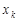при то этот предел называется частной производной функции 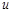в точке по аргументу 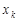и обозначается одним из следующих символов:

, , , .

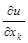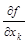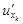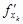Таким образом

.

Отметим, что частная производная функции 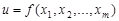по аргументу 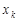представляет собой обыкновенную производную функции одной переменной 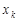при фиксированных значениях остальных переменных. Поэтому вычисление частных производных производится по обычным правилам вычисления производных функций одной переменной.

Пример. Найти частные производные функции .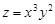

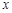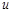Чтобы найти частную производную по зафиксируем переменную . Далее, рассматривая как функцию одной переменной 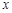, получим

.

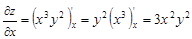Заметим, что 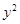можно вынести за знак производной именно потому, что мы при дифференцировании по 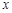мы считаем переменную постоянной.

Зафиксировав переменную 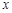найдем частную производную по переменной

.

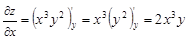Дата добавления: 2014-01-07