Специфические аксиомы и теоремы алгебры логики

Как любую логическую функцию можно реализовать при помощи соответствующей комбинации элементарных логических функций, так и любую логическую схему можно сформировать при помощи соответствующей комбинации элементарных логических элементов.

Система логических функций называется функционально полной, если с помощью функций, входящих в эту систему, применяя операции суперпозиции и подстановки, можно получить любую сколь угодно сложную логическую функцию.

Подстановка в логическую функцию вместо ее аргументов других логических функций называется суперпозицией.

Элементы, реализующие простейшие логические функции, схематически представляются в виде прямоугольников, на поле которых изображается символ, обозначающий функцию, выполняемую данным элементом. На рис. 8.1 показаны условные обозначения элементов, реализующих логические функции «И», «ИЛИ», «НЕ». Входные переменные принято изображать слева, а выходные - справа. Считается, что передача информации происходит слева на право.

Рис. 8.1. Условные обозначения элементов, реализующих логические функции «И», «ИЛИ», «НЕ»

При переходе от логических функций к логическим схемам обычно принимается, что логической единице (1) соответствует импульсный сигнал стандартной амплитуды, например, высокого уровня, а логическому нулю (0) - низкого уровня и обычно фиксированной длительности. Причем, все входные сигналы должны поступать на каждый элемент одновременно.

Свойства элементарных функций алгебры логики

В алгебре логики имеются четыре основных закона: переместителъный (свойства коммутативности); сочетательный (свойства ассоциативности); распределительный (свойства дистрибутивности); инверсии (правило де Моргана).

Некоторые законы обычной алгебры применимы и к алгебре логики.

Переместителъный закон:

для умножения ;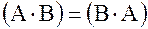

для сложения (А+В) = (В+А).

Сочетательный закон:

для умножения

для сложения А+(В+С)=(А+В)+С.

Распределительный закон:

;

.

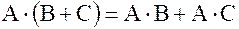Алгебра логики имеет ряд специфических аксиом и теорем, основные из которых, необходимые для анализа и синтеза логических цепей или схем, приведены в таблице 8.11.

Аксиомы и теоремы, записанные во второй колонке табл. 8.11 (т.е. слева), называются двойственными аксиомам и теоремам, записанным в третьей колонке (т.е. справа).

Двойственность определяется как изменение всех знаков операции «И» на знаки операции «ИЛИ», всех знаков операции «ИЛИ» на знаки операции «И», всех нулей на единицы и всех единиц на нули.

Двойственность является одним из основных свойств алгебры логики и означает, что если 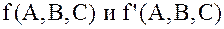- двойственные функции, то:

.

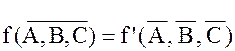Таблица 8.11.

Законы де Моргана являются одной из иллюстраций свойства двойственности и, как уже отмечалось, могут быть сформулированы в виде:

Из законов Моргана следует, что, имеется возможность выражать конъюнкцию через дизъюнкцию и отрицание, или дизъюнкцию - через конъюнкцию и отрицание. Законы де Моргана и следствия из них справедливы для любого количества переменных.

Функция сложения по модулю 2 представляется следующим образом:

.

Для этой функции справедливы следующие аксиомы:

.

На основании рассмотренных аксиом и свойств элементарных логических функций можно, например, вывести правила представления функций «И», «ИЛИ», «НЕ» через функцию сложения по модулю 2 и наоборот:

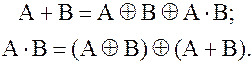
Функции «И», «ИЛИ», «НЕ» через функцию Шеффера выражаются следующим образом:

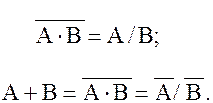
Функция Пирса может описываться следующими выражениями:

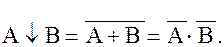
Для этой функции справедливы следующие аксиомы:

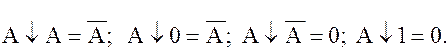
Функции «И», «ИЛИ», «НЕ» выражаются через функцию Пирса следующим образом:

Следует отметить, что логические выражения, содержащие операции дизъюнкции и конъюнкции, можно преобразовывать (раскрывать скобки, выносить общий множитель, переставлять местами члены и т.д.) по правилам алгебры, считая формально дизъюнкцию операцией сложения, а конъюнкцию - операцией умножения. В алгебре логики, в отличие от обыкновенной алгебры, знак + либо знак 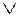означают логическую связку «ИЛИ», а знак умножения "•" либо знаки и &, означают логическую связку «И».

Дата добавления: 2014-01-07