Пример. Представить функцию Шеффера в виде многочлена

Следовательно, СНКФ - это стандартное или каноническое произведение макстермов максимального ранга данной функции, а СНДФ - стандартная или каноническая сумма минтермов максимального ранга данной функции.

Запись СДНФ по ее таблице истинности можно произвести следующим образом. Следует для всех комбинаций входных переменных, обращающих функцию в единицу, записать элементарные произведения, инвертируя переменные, принимающие на данной комбинации нулевое значение, а все полученные элементарные произведения соединить знаками логического суммирования. Применив данное правило к функции, представленной в табл. 8.14, получим три элементарные произведения:

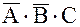- первое элементарное произведение;

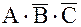- второе элементарное произведение;

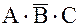- третье элементарное произведение.

Если соеднить эти произведения знаками логического суммирования, то получится исходное выражение:

.

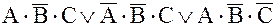Таким образом, СНДФ функции находят следующим образом: выписывается ряд произведений, т.е. минтермов, всех аргументов и соединяются знаками дизъюнкции. Количество произведений должно равняться числу наборов, на которых заданная функция равна единице. В каждом минтерме над аргументом, значение которого в данном наборе равнялось нулю, ставится знак отрицания.

СНКФ функции формируют следующим образом: формируется произведение дизъюнкций, т.е. макстермов, всех аргументов с количеством сомножителей, равным числу наборов, на которых заданная функция обращается в ноль. В каждом макстерме над аргументом, равным единице в данном наборе, ставится знак отрицания.

Произвольная НДФ переводится в СНДФ следующим образом.

Пусть - минтерм функции, представленной в НДФ. Тогда этот минтерм преобразуется следующим образом:

, (8.2)

где - переменная, которая не входит в минтерм .

Если максимальный ранг для функции равен 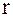, а минимальный ранг j-го минтерма равен k, то преобразование (8.2) необходимо применить к j-му минтерму раз.

Пример. Преобразуем логическую функцию, заданную в НДФ:

Поскольку терм F₄ имеет максимальный ранг и в него входят все переменные функции, то воспользуемся приемом преобразования поочередно к остальным трем термам:

.

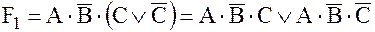Оба члена полученного выражения умножим на . В результате получим:

.

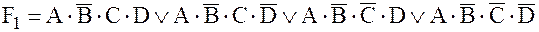Аналогично рассмотрим термы и .

.

.

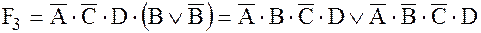После приведения подобных членов определяем СНДФ данной функции:

Произвольная НКФ переводится в СНКФ путем следующего преобразования:

Пусть задан макстерм .

Тогда .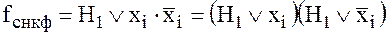

Преобразуем в СНКФ логическую функцию:

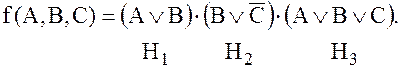
Применяем правило преобразований поочередно к макстермам 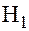и , так как макстерм , имеет максимальный ранг:

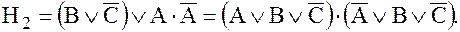
После упрощений СНКФ функция примет окончательный вид:

.

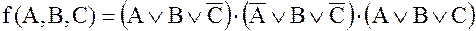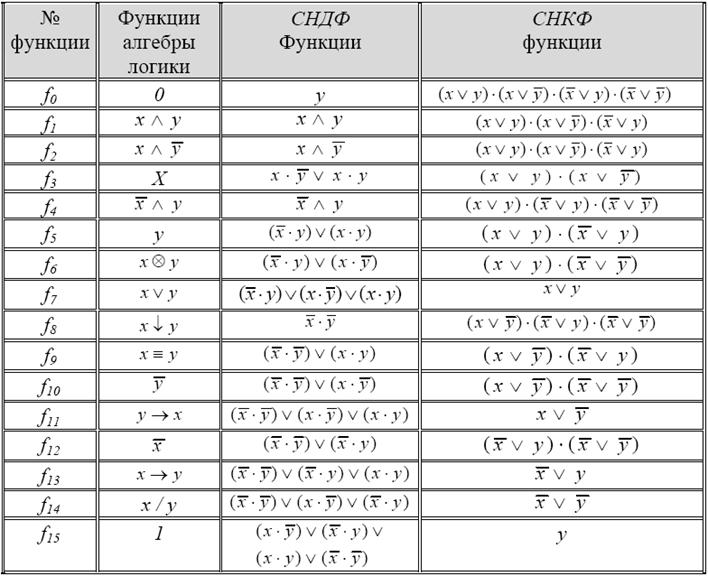
В таблице 8.15 приведены СНКФ и СНДФ для элементарных логических функций.

Таблица 8.15.

СНКФ и СНДФ для элементарных логических функций

Системы функций алгебры логики

Любая логическая функция может быть представлена многочленом вида:

где 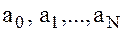– некоторые константы, равные нулю или единице;

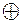- знак операции сложения по модулю два.

При записи конкретной логической функции в виде многочлена коэффициенты 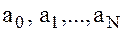выпадают, т.к. члены при которых эти коэффициенты равны нулю, можно опустить, а коэффициенты, равные единице, не писать.

Чтобы логическую функцию, заданную таблицей ее значений, представить в виде многочлена, следует эту функцию записать в виде суммы конституант единицы (равных единице на тех же наборах, на которых равна единице заданная функция). Затем все аргументы, входящие в полученное выражение с отрицанием, заменить с помощью соотношения , раскрыть скобки и привести подобные члены с учетом, что в данном случае 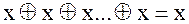, если n – нечетно и , если n четно.

.

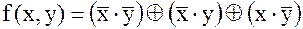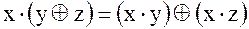Используя соотношения и , после преобразований получим следующее выражение:

.

Приводя подобные члены, окончательно получим:

Класс линейных функций (К_л)

Логическая функция называется линейной, если она представляется полиномом первой степени:

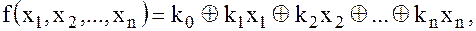
где коэффициенты равны нулю или единице.

Функции двух аргументов, которые являются линейными, приведены в таблице 8.13.

Таблица 8.13.

Дата добавления: 2014-01-07