
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Это выполняется когда направления противоположны
 |
б) Произведение двух комплексных чисел получается по правилу умножения многочленов, учитывая, что i2 = -1:

Если комплексные числа заданы в тригонометрической форме:
 (6)
(6)

Модуль произведения комплексных чисел равен произведению модулей этих чисел, а аргумент произведения равен сумме аргументов сомножителей: 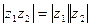 .
.
Доказательство:
z1 = (a, b); z2 = (c, d);
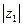 =
=  ;
;  =
= 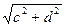 ;
;
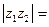
В показательной форме:
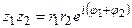
в) Деление комплексных чисел вводится как операция, обратная умножению:
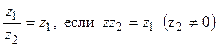
В алгебраической форме для нахождения частного двух комплексных чисел, записанных в алгебраической форме, нужно делимое и делитель умножить на число, сопряженное с делителем:
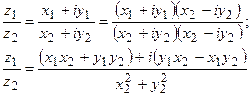
Пример: Вычислить:

Пусть числа z 1 и z 2 заданы в тригонометрической форме (6). Найдём модуль и аргумент частного. По определению:
 и
и  .
.
Отсюда:  и
и 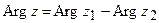 .
.
Модуль частного двух комплексных чисел равен частному модулей этих чисел, а аргумент частного равен разности аргументов делимого и делителя.
 или
или 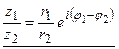
г) Возведение комплексных чисел в натуральную степень.
Целая положительная степень комплексного числа определяется так же, как и действительного:  . Т.е. возведение комплексного числа в целую положительную степень является распространением правила умножения комплексных чисел на случай, когда все
. Т.е. возведение комплексного числа в целую положительную степень является распространением правила умножения комплексных чисел на случай, когда все 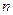 множителей одинаковы. В алгебраическом представлении возведение комплексного числа в n -ую степень производится по алгебраическим правилам перемножения многочленов.
множителей одинаковы. В алгебраическом представлении возведение комплексного числа в n -ую степень производится по алгебраическим правилам перемножения многочленов.
Например: 
 и т.д. В общем случае:
и т.д. В общем случае:
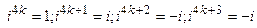 .
.
В тригонометрическом представлении модуль n -ой степени комплексного числа равен n - ой степени модуля исходного комплексного числа, а аргумент n -ой степени комплексного числа получается посредством умножения на 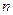 аргумента исходного комплексного числа. В итоге получается формула Муавра:
аргумента исходного комплексного числа. В итоге получается формула Муавра:
|
|
|
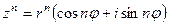 .
.
Пусть число z задано в тригонометрической форме: 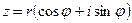 .
.
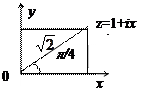
Отсюда:
 .
.
Рис. 4
В показательном представлении операции с модулями и аргументами комплексных чисел при делении совпадают с таковыми при делении в тригонометрическом виде:
 .
.
В показательном представлении имеем:
 .
.
Таким образом, комплексное число z 0 имеет ровно n корней степени n, получаемых из вышеприведенной формулы. Следует отметить, что все значения корня лежат на окружности радиуса ρ =
0 имеет ровно n корней степени n, получаемых из вышеприведенной формулы. Следует отметить, что все значения корня лежат на окружности радиуса ρ =  и делят окружность на n равных частей
и делят окружность на n равных частей
 . Запишем число z =1+ i в тригонометрическом виде. Здесь
. Запишем число z =1+ i в тригонометрическом виде. Здесь 
 =
= 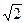 ,
,
tg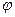 = 1;
= 1;  ; z =
; z =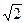
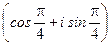 (рис. 4).
(рис. 4).
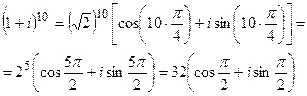
Пример 2. Вычислить 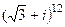 .
.
Запишем число  в тригонометрическом виде, учитывая при этом, что
в тригонометрическом виде, учитывая при этом, что 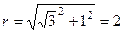
 ,
, 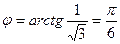 ,
,  .
.
Произведя по указанным правилам возведение в двенадцатую степень комплексного числа, имеем
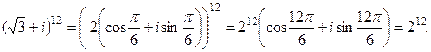
Пример 3. Найти действительную и мнимую части комплексного числа 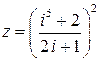 .
.
Заметим сначала, что  . Таким образом,
. Таким образом,
 .
.
Значит,  .
.
д) Извлечение корня.
Корнем n-ой степени из комплексного числа z называется такое число w (w= ), что wn=z.
), что wn=z.
Пусть числа z и w представлены в тригонометрической форме:
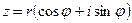 и
и 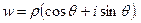
Найдём ρ и q. Так как

Поэтому: ρ =  - арифметическое значение корня из положительного числа r, а q =
- арифметическое значение корня из положительного числа r, а q = (k=
(k= ). Т.о.
). Т.о.
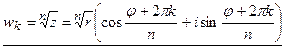 или
или
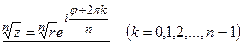
Значение qк, дающие существенно различные значения корня n -ой степени из z соответствуют только n значениям k (0,1,2,… n -1). Остальным целым k соответствуют значения qk, отличающиеся от одного из указанных значений на величину, кратную 2 π.
Проверить, например, что wn = w 0!
Таким образом, комплексное число z 0 имеет ровно n корней степени n, получаемых из этих формул. Из формул вытекает, что все значения корня лежат на окружности радиуса ρ =
0 имеет ровно n корней степени n, получаемых из этих формул. Из формул вытекает, что все значения корня лежат на окружности радиуса ρ =  и делят окружность на n равных частей.
и делят окружность на n равных частей.
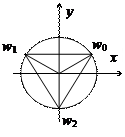
Пример 1: Вычислить  . Запишем число в тригонометрической форме:
. Запишем число в тригонометрической форме:

|
|
|
Рис.5.

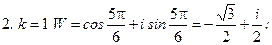
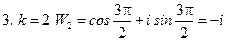
Пример 2: Вычислить  . Запишем число в показательной форме:
. Запишем число в показательной форме:


Рис. 6.
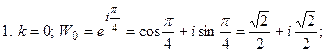
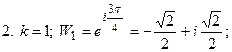
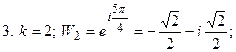
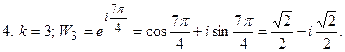
Пример 2. Решить систему уравнений

Решим систему по правилу Крамера. Найдем
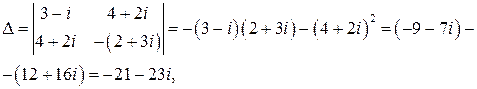

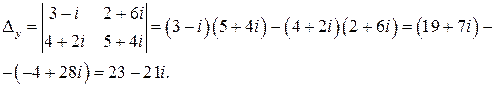
Таким образом,
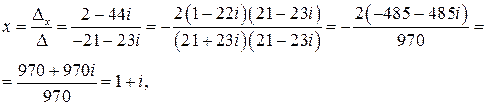
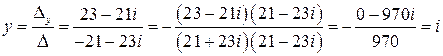 .
.
Значит, решением системы будет пара комплексных чисел 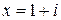 ,
, 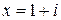 .
.
Пример 3. Найти комплексное число 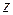 , удовлетворяющее уравнению
, удовлетворяющее уравнению 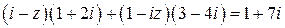 , и записать его в алгебраической и тригонометрической формах.
, и записать его в алгебраической и тригонометрической формах.
Раскрывая скобки в левой части и приводя подобные члены, получим 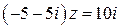 , откуда
, откуда
 .
.
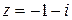 - это найденное число в алгебраической форме.
- это найденное число в алгебраической форме.
Найдем  , тогда тригонометрическая форма числа
, тогда тригонометрическая форма числа 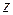 будет иметь вид:
будет иметь вид:  .
.
комплексного числа
Использование формулы Эйлера 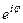 =
=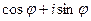 позволяет перейти от тригонометрической формы записи комплексного числа к показательной или экспоненциальной форме:
позволяет перейти от тригонометрической формы записи комплексного числа к показательной или экспоненциальной форме:
 ,
,
где 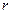 =
= - модуль комплексного числа, а угол
- модуль комплексного числа, а угол 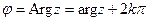 (
( ). В силу формулы Эйлера функция
). В силу формулы Эйлера функция  является периодической с основным периодом
является периодической с основным периодом 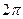 .
.
Пример 4. Записать комплексное число  ί в показательном виде.
ί в показательном виде.
Решение: 
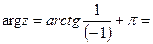
 . Поэтому
. Поэтому  ί=
ί=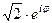 .
.
Пример 5. Найти произведение комплексных чисел 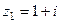 и
и 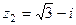 , предварительно перейдя к тригонометрическому представлению.
, предварительно перейдя к тригонометрическому представлению.
Решение: 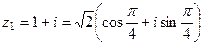 ,
, 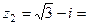
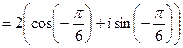 .
.
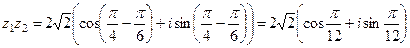 .
.
В показательном представлении операции с модулями и аргументами комплексных чисел при делении совпадают с таковыми при делении в тригонометрическом виде:
 .
.
Возведение комплексного числа в целую положительную степень является распространением правила умножения комплексных чисел на случай, когда все 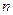 множителей одинаковы. В алгебраическом представлении возведение комплексного числа в n -ую степень производится по алгебраическим правилам перемножения многочленов с учетом того, что
множителей одинаковы. В алгебраическом представлении возведение комплексного числа в n -ую степень производится по алгебраическим правилам перемножения многочленов с учетом того, что
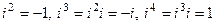 .
.
В тригонометрическом представлении модуль n -ой степени комплексного числа равен n - ой степени модуля исходного комплексного числа, а аргумент n -ой степени комплексного числа получается посредством умножения на 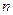 аргумента исходного комплексного числа. В итоге получается формула Муавра:
аргумента исходного комплексного числа. В итоге получается формула Муавра:
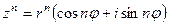 .
.
В показательном представлении имеем:
 .
.
Таким образом, комплексное число z 0 имеет ровно n корней степени n, получаемых из вышеприведенной формулы. Следует отметить, что все значения корня лежат на окружности радиуса ρ =
0 имеет ровно n корней степени n, получаемых из вышеприведенной формулы. Следует отметить, что все значения корня лежат на окружности радиуса ρ =  и делят окружность на n равных частей.
и делят окружность на n равных частей.
Пример 6. Вычислить  .
.
|
|
|
Решение: Запишем число 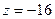 в тригонометрической форме:
в тригонометрической форме: 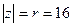 ,
,  ,
,  .
.
Поэтому  ,
,  .
.
При 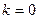 имеем
имеем
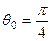 ,
, 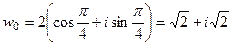 .
.
При 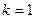 имеем
имеем
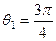 ,
, 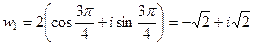 .
.
При 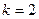 имеем
имеем
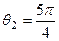 ,
,  .
.
При 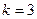 имеем
имеем
 ,
,  .
.
 |
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 402; Нарушение авторских прав?; Мы поможем в написании вашей работы!