Дифференциальное уравнение массообмена

Выделим в потоке данной фазы элементарный параллепипед с ребрами dx, dy и dz, ориентированными относительно осей координат, как показано на рис. 2.3.

Рассмотрим материальный баланс по распределяемому веществу для параллепипеда при установившемся массообмене. Распределяемое вещество проходит сквозь грани параллепипеда как путем турбулентной диффузии, так и путем молекулярной диффузии.

Обозначим концентрацию распределяемого вещества в плоскости левой грани площадью dydz через с и проекции скорости на оси координат для данного элемента (точки) потока – через w_х,, w_y,, w_z соответственно.

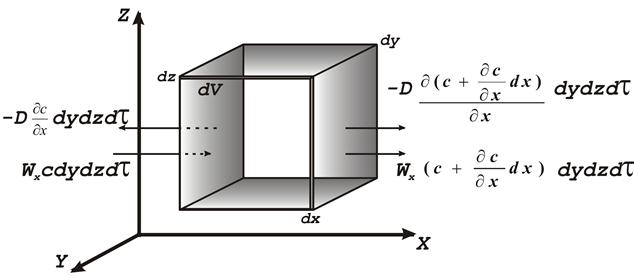
Рис.2.3. К выводу дифференциального уравнения

массообмена в движущейся среде

Тогда количество вещества, поступающего только путем турбулентной диффузии через площадь dydz, т.е. в направлении оси х, за время dt составляет:

M_x = w_xdydzcdt

На противоположной грани параллепипеда скорость в направлении оси х равна w_х+(w_х/ х)dx и концентрация распределяемого вещества составляет с+с/х)dx. Следовательно за время dt через противоположную грань параллепипеда выходит путем турбулентной диффузии количество вещества равное:

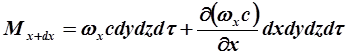
Разность между количествами вещества, прошедшего через противоположные грани параллепипеда за время dt в направлении оси х, равна

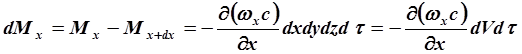
где dV = dxdydz – объем элементарного параллепипеда.

Аналогично в направлении осей y и z:

; .

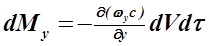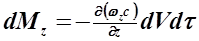Таким, образом содержание распределяемого вещества в объеме параллепипеда измениться за время dt вследствие перемещения вещества только путем турбулентной диффузии на величину

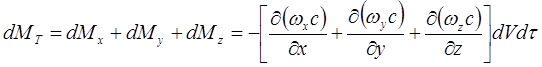
или в развернутом виде

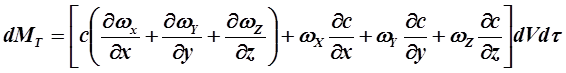
Согласно уравнению неразрывности потока для установившегося движения:

Следовательно, предыдущее выражение dM_к примет вид

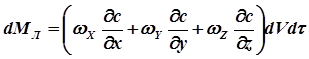(А)

Количество распределяемого вещества, поступающего в параллепипед только путем молекулярной диффузии через грань dydz за время dt составляет:

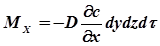
Количество вещества, выходящего за то же время путем молекулярной диффузии через противоположную грань составляет

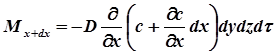
Разность между количествами продиффундировавшего через противоположные грани параллелепипеда вещества в направлении оси х за время dt равна:

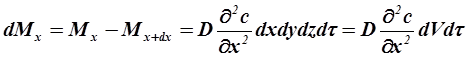
Аналогично в направлении осей y и z:

;

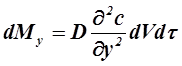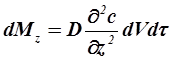
Количество распределяемого вещества в объеме всего параллепипеда за время dt измениться при переносе путем молекулярной диффузии на величину:

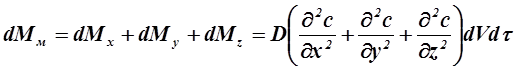(Б)

Изменением количества распределяемого вещества за счет турбулентной диффузии в объеме параллепипеда (его накопление или убыль) должно компенсироваться соответственно отводом или подводом такого же количества вещества через грани параллепипеда путем молекулярной диффузии, т.е. должно соблюдаться условие:

dM_T +dM_M =0

В противном случае концентрация распределяемого вещества в любой точке параллепипеда стала бы изменяться во времени, в то время как при установившемся процессе она является только функцией координат точки, т.е.:

с =f(x, y, z)

Таким образом

dM_T = - dM_M

и приравняв выражения (А) и (Б) получим

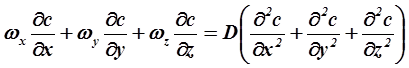(2.11)

или в более краткой записи:

w grad c = D Ѳc (2.12)

Уравнение (2.11) представляет собой дифференциальное уравнение конвективного массообмена, или дифференциальное уравнение массообмена в движущейся среде. Оно выражает закон распределения концентрации данного компонента в движущейся среде при установившемся процессе массообмена.

Для неустановившегося процесса массообмена (но протекающего в условиях стационарного потока фазы) левая часть уравнения (2.11) должна быть дополнена членом 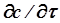, отражающим локальное изменение концентрации распределяемого вещества во времени. Тогда уравнение (2.11) примет вид:

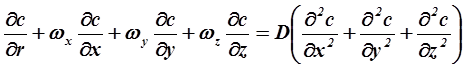(2.13)

Уравнение (2.13) по структуре аналогично дифференциальному уравнению конвективного теплообмена (уравнению Фурье-Кирхгофа). Отличием является то, что в уравнение (2.13) вместо температурного градиента входит градиент концентрации, а вместо коэффициента температуропроводности а – коэффициент молекулярной диффузии D.

При массообмене в неподвижной среде w_C = w_U = w_Z = и конвективная составляющая в левой части уравнения (2.13) равна нулю, и уравнение обращается в дифференциальное уравнение молекулярной диффузии:

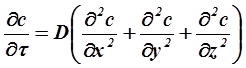(2.14)

Уравнение (2.14) носит название второго закона Фина.

В дифференциальном уравнении массообмена в движущейся среде, помимо концентрации, переменной является скорость потока. Поэтому данное уравнение надо рассматривать совместно с дифференциальным уравнением гидродинамики: уравнениями движения Навье-Стокса и уравнением неразрывности потока. Однако эта система уравнений не имеет аналитического решения и для получения расчетных зависимостей по массообмену приходится прибегать к преобразованию дифференциального уравнения массообмена в движущейся среде методами теории подобия.

Дата добавления: 2014-01-07