Нормальный законы распределения

Равномерный, показательный и

Перспективы повышения качества жилища

Направления совершенствования качества жилища обусловлены экономической и политической ситуацией. Сегодня Россия находится на стадии перехода от общества с централизованной плановой экономикой на основе индустриально-конвейерного производства к обществу с децентрализованной рыночной экономикой на основе научно-информационного производства и экологических принципов.

В этой связи можно указать перспективные направления в формировании жилища, связанные с переходом от массового жилища для трудящихся к индивидуальному жилищу различного уровня комфорта для основных слоёв общества. Таким образом, перспективные на-правления будут определять пути развития типологии от единообразного многоэтажного жи-лища к разнообразному - малоэтажному, среднеэтажному и многоэтажному.

Основными направлениями совершенствования качества жилища являются:

1) новая функциональная и пространственная организация элементов жилища, основанная на гибкости и мобильности планировочных решений. Развитие помещений для активного отдыха и профессионального труда в соответствии с социальными требованиями ведущих социально-профессиональных групп; многообразие в типологии жилища;

2) максимальное взаимопроникновение искусственной и естественной среды на всех уровнях жилища, объединение качеств основного и второго жилища. Квартиры с развитыми открытыми пространствами семейного пользования, дома с летними помещениями соседского пользования (террасы, галереи) и двор общего пользования;

3) разнообразие типов жилища и составляющих элементов в жилой ячейке, доме и районе на основе всестороннего учёта потребностей населения. Социальная адресность, проектирование для конкретных социальных групп и слоёв (малоимущие, средний класс, элита) и для различных форм и видов активного отдыха;

4) структурная дифференциация и индивидуализация свободных междомовых пространств. Структурность и иерархичность открытых пространств: дом - двор, улица - двор - приквартирный участок;

5) индивидуализация и оригинальность архитектурного облика жилой застройки, повышение её эстетической выразительности. Выразительная внешняя форма как отражение мастерства и социальных требований (потребителя); простота форм при сложности культурных символов.

Равномерное распределение. Функция плотности вероятности равномерного закона равна:

(10.17)

где a и b – данные числа, a < b; a и b – параметры равномерного закона.

Найдем функцию распределения F (x) равномерного закона. Если х £ a, то

. Если a < x < b, то .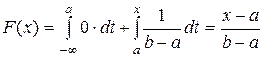

Когда x ³ b, . Итак,

(10.18)

Графики функций F (x) и f (x) показаны на рис. 10.10.

Определим числовые характеристики равномерного распределения.

. (10.19)

; (10.20)

. (10.21)

Рис. 10.10

Вероятность попадания в интервал (α, β) равномерно распределенной случайной величины задается следующей, легко выводимой формулой:

(10.22)

Равномерным распределением можно аппроксимировать ошибки измерений, когда измеренное значение округляют до ближайшего целого на шкале измерительного прибора.

Найдем закон распределения линейной функции Y равномерно распределенной случайной величины Х, Y = (cX + d), где с, d – данные числа.

Если 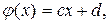то 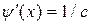. Когда значения случайной величины Х принадлежат интервалу (a, b), значения случайной величины Y принадлежат интервалу (ca + d; cb +d); следовательно,

, если ; в противном случае .

Вновь получено равномерное распределение – на этот раз на интервале (ca + d, cb + d). (Если c < 0, то левая граница интервала – число cb +d, правая - число ca + d).]

10.7.2. Показательное распределение. Случайная величина Х имеет показательное распределение, если ее плотность вероятности задается формулой

(10.23)

Параметр закона λ должен быть больше нуля.

Опишем функцию распределения F (x) показательного закона. Если х £ 0, то, очевидно, F (x) = 0. Пусть х > 0. Тогда

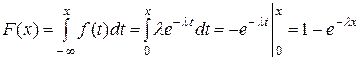, таким образом

(10.24)

Графики функций F (x) и f (x) показаны на рис. 10.11.

Рис. 10.11

Найдем числовые характеристики показательного распределения.

. (10.25)

.

; . (10.26)

Вероятность попадания в интервал (α, β), , равна

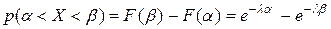. (10.27)

Показательное распределение используется, например, в теории массового обслуживания.

Нормальное распределение. Случайная величина Х распределена по нормальному закону (закону Гаусса), если ее плотность вероятности задается формулой

, ,

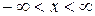где 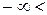а < ¥ и σ > 0 – параметры закона.

График функции плотности вероятности нормального закона показан на рис. 10.12. График симметричен относительно прямой х = а.

Рис. 10.12

Математическое ожидание нормального закона равно значению параметра а. D (X) = σ ², σ (X) = σ. Среднее квадратическое отклонение нормально распределенной случайной величины равно значению параметра σ.

Вычислим вероятность того, что нормально распределенная случайная величина Х примет значение из интервала (α, β).

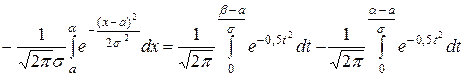
Функция

(10.28)

называется функцией Лапласа. Для нее составлены таблицы (приложение 1), по которым, зная аргумент х, можно найти величину Φ (х). Можно, конечно, решить обратную задачу: по значению функции Лапласа найти значение аргумента.

Укажем три простых свойства функции Лапласа:

1. .

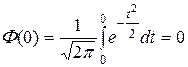2. .

На самом деле уже для значений аргумента х ³ 5 можно считать, что .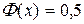

3. .

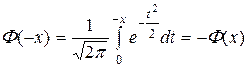Таким образом, функция Лапласа нечетна.

Мы показали, что

. (10.29)

Теперь легко описать функцию распределения 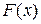нормального закона с параметрами a и s. В самом деле

.

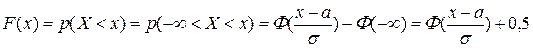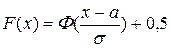(10.30)

В некоторых пособиях по теории вероятностей приводятся таблицы

Для интервала |Х - а| < δ имеем 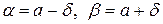, поэтому

. (10.31)

Нормальное распределение довольно часто встречается при решении практических задач. В приложении приведена таблица нормального распределения (таблица функции Лапласа).

Дата добавления: 2014-01-07