Шесть функций сложного процента

Во всех вычислениях с использованием сложного процента используется формула:

,

где 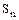– сумма после n периодов;

i – периодическая ставка дохода;

n – количество периодов накоплений.

2.1. Будущая стоимость денежной единицы (накопленная сумма единицы)

Данная функция позволяет определить будущую стоимость инвестированной денежной единицы, исходя из предполагаемых ставки дохода, срока накопления и периодичности начисления процента:

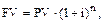
где FV – будущая стоимость денег;

PV – текущая стоимость денег.

Справедливость этого утверждения очевидна. Если на депозит положена сумма PV, то через один период начисления эта сумма станет равна:

,

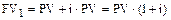через два периода она станет равна:

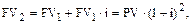
и так далее:

…………………………………..

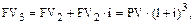
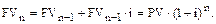
Пример. $1000 вложено в банк под 10 % годовых. Какая сумма накопится на счете через 5 лет?

,

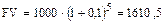Правило 72-х.

Иногда при расчетах приходится сталкиваться с задачей определения количества периодов начисления, по истечении которых первоначально депонированная сумма увеличивается вдвое. Очень просто решить эту задачу позволяет известное “Правило 72-х”, в основу которого положены логарифмы. Количество периодов, необходимое для удвоения первоначальной суммы вычисляется так:

.

Данное правило показывает точные результаты при значениях i: 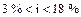. Срабатывает правило и в обратном порядке для определения ставки дохода, при которой депонированная сумма удвоится.

Более частое, чем один раз в год, начисление процентов.

Приведенные выше расчеты основывались на том предположении, что начисление процентов происходит один раз в год. Однако аккумулирование может происходить не только раз в год, но и чаще, например раз в квартал, раз в месяц и т. д. В этом случае формула будет выглядеть следующим образом:

,

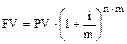где m – частота начисления процентов в год;

n – число лет, в течение которых происходит накопление.

Чем чаще начисляются проценты, тем больше накопленная сумма.

2.2. Будущая стоимость аннуитета (накопление единицы за период)

Часто бывает, что мы имеем дело не с единичным платежом, произведенным в определенный момент времени, а с серией платежей, происходящих в различные моменты времени. Если эти платежи происходят через строго определенные промежутки времени, то такая серия называется аннуитетом.

Платежом k-го периода называется единовременный денежный вклад в этом периоде. Он обозначается через РМТ (payment).

Аннуитеты разделяются на следующие категории: равномерные и неравномерные, обычные и авансовые. Равномерным аннуитетом называется аннуитет, состоящий из серии равновеликих платежей. Противоположностью ему является неравномерный аннуитет, при котором величина платежей может быть разной в различных платежных периодах. Аннуитет называетсяобычным, если платежи осуществляются в конце каждого платежного периода, и авансовым, если платежи осуществляются в начале платежного периода.

Вторая функция сложного процента показывает, какой будет стоимость серии равных сумм, депонированных в конце каждого из периодических интервалов, по истечении установленного срока.

Очевидно, что будущая стоимость по окончании первого платежного периода (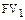) будет равна:

,

далее:

……………………………

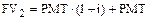
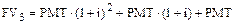
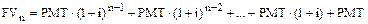
В данном случае имеет место геометрическая прогрессия, поэтому, применив известную из курса математики формулу суммы членов геометрической прогрессии, можно получить выражение для будущей стоимости обычного n -периодного аннуитета:

.

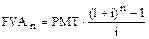Пример. Если вкладывать ежегодно $900 на счет в банке под 10 % годовых, сколько накопится на нем через 5 лет?

.

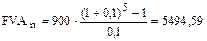Теперь перейдем к рассмотрению авансового аннуитета. Как и в случае обычного, рассмотрим накопленные суммы в конце первого, второго... n -го периода:

,

,

,

……………………….

.

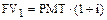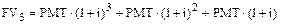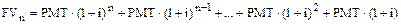Применив формулу суммы геометрической прогрессии, получаем:

.

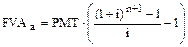Периодические депозиты могут вноситься чаще, чем один раз в год, соответственно чаще накапливается процент. Тогда ранее полученная формула имеет вид:

.

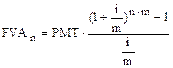Чем чаще делаются взносы, тем больше накопленная сумма.

Пример. Если вкладывать ежемесячно $75 на счет в банке под 10 % годовых, сколько накопится на нем через 5 лет?

.

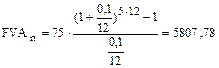2.3 Фактор фонда возмещения

Данная функция позволяет рассчитать величину периодического платежа, необходимого для накопления нужной суммы по истечении n платежных периодов при заданной ставке процента.

Из формулы будущей стоимости аннуитета можно сделать вывод, что величина каждого платежа (SFF) в случае обычного аннуитета вычисляется следующим образом:

.

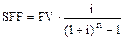Пример. Необходимо за 4 года скопить $1000 при ставке банка 10 %. Сколько придется вкладывать каждый год?

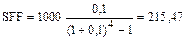
В случае авансового фонда возмещения (соответствующего авансовому аннуитету) формула единичного платежа (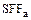) имеет вид:

.

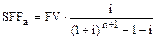2.4 Текущая стоимость единицы (реверсии)

Текущая стоимость единицы – это величина, обратная накопленной сумме единицы, то есть текущая стоимость единицы, которая должна быть получена в будущем:

,

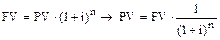Пример. Сколько нужно вложить на счет в банке, приносящий 10% годовых, чтобы через 5 лет на нем было $100.

.

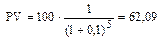При более частом накоплении:

.

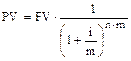Чем выше частота дисконтирования, тем меньше необходимая сумма текущей стоимости денежной единицы.

2.5 Текущая стоимость аннуитета

Часто бывает так, что требуется оценить текущую стоимость серии платежей, т. е. аннуитета. Как и в случае будущей стоимости аннуитета, аннуитет может быть обычный и авансовый.

Очевидно, что текущая стоимость n -периодного обычного аннуитета равна сумме текущих стоимостей всех платежей. Обозначим текущую стоимость k -го платежа как PV_k. Тогда текущая стоимость каждого платежа будет равна:

,

,

....................

,

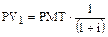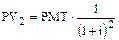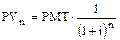а текущая стоимость аннуитета

.

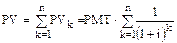Применив к этому выражению формулу суммы членов геометрической прогрессии, получаем искомое выражение для текущей стоимости аннуитета:

.

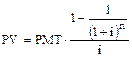Пример. Ежегодный платеж за аренду дачи составляет $1000, ставка 10%, срок аренды 2 года. Определить текущую стоимость платежей.

.

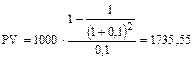Аналогично обычному аннуитету, вычисляется текущая стоимость для авансового аннуитета:

.

2.6. Взнос на амортизацию единицы

Амортизация – процесс погашения (ликвидации) долга в течение определенного периода времени.

Данная функция позволяет определить, каким будет обязательный периодический платеж по кредиту, включающий выплату процентов и части основной суммы долга, и позволяющий погасить кредит в течение установленного срока.

Оказывается, для того, чтобы аннуитет погашал кредит, текущая стоимость этого аннуитета должна быть равна первоначальной сумме кредита. Используя формулу текущей стоимости аннуитета, мы можем получить величину периодического платежа – взноса на амортизацию капитала:

.

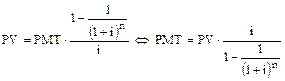Каждый платеж состоит из двух частей:

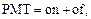
где on – погашение процентов;

of – погашение кредита.

Пример. Какова величина ежегодного взноса в погашение кредита $15000, предоставленного на 5 лет под 10 % годовых.

.

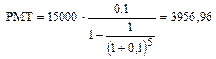Используя аналогичные рассуждения, можно получить величину взноса на амортизацию капитала для авансового аннуитета:

.

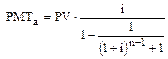Дата добавления: 2014-01-07