Понятие непрерывности функции

Непрерывность функций

Лекция 14.

Понятие непрерывности функций.Точки разрыва функции и их классификация.

Понятие непрерывности функции является одним из основных понятий математического анализа.

Определение. Функция у=f(x), определённая на интервале (а;b), называется непрерывной в точке х₀(а;b), если 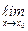f(x) = f(x₀).

Пример. Доказать непрерывность функции f(x) = 2х² + 2х +1 в точке х₀ =1.

Решение. Находим:

1) 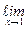f(x) = 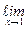(2х² + 2х +1) = 2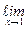x² + 2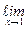x + 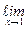1 = 2×1 + 2×1 + 1 = 5.

2) f(1) = 2×1² + 2×1 + 1 = 5.

Так как 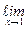f(x) = f(1), то по определению функция f(x) непрерывна в точке х₀ =1.

Определение. Пусть х₀, х₀Î(а;b). Разность ∆х = х − х₀ называется приращением аргумента в точке х₀, а разность ∆у =f(x) − f(x₀) = f(x₀ + ∆x) − f(x₀) ─ приращением функции в точке х_0.

Теорема 1. Функция у = f(x) непрерывна в точке х₀Î(а;b) тогда и только тогда, когда ∆у = 0.

Доказательство. 1) Пусть функция у = f(x) непрерывна в точке х₀Î(а;b). Это означает, что 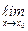f(x) = f(x₀). Положим х = х₀ + ∆х. Получим

f(x₀ + ∆x) = f(x₀),

откуда

f(x₀ + ∆x) − f(x₀) = 0,

((x₀ + ∆x) − f(x₀)) = 0,

т.е.

∆у = 0.

2) Пусть теперь ∆у = 0. Тогда ((x₀ + ∆x) − f(x₀)) = 0, откуда f(x₀ + ∆x) − −f(x₀) = 0, f(x₀ + ∆x) = f(x₀). Это означает, что функция у = f(x) непрерывна в точке х₀.

Теорема 2. Если функции f(x) и φ(х) непрерывны в точке х₀, то непрерывны в это точке их сумма f(x) + φ(x), разность f(x) − φ(x), произведение f(x)×φ(x), а также частное f(x)/φ(x) при условии, что φ(х₀) ≠ 0.

Доказательство этой теоремы непосредственно следует из определения непрерывности и свойств пределов функций.

Например, непрерывными являются многие элементарные функции:

1) целая рациональная функция P_n(x) = 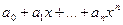непрерывна при всех хÎR;

2) дробно-рациональная функция

R(x) =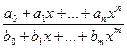

непрерывна при всех х, для которых знаменатель не обращается в нуль;

3) тригонометрические функции у = sinx, y = cosx, y = tgx, y = ctgx непрерывны во всех точках области определения.

Теорема 3. Пусть функция z = φ(x) непрерывна в точке х₀, а функция у = f(z) непрерывна в точке z₀ = φ(x₀). Тогда сложная функция у = f(φ(x)) непрерывна в точке х₀.

Эта теорема позволяет сделать вывод о непрерывности функций, которые являются композициями непрерывных функций.

Пример. Доказать, что функция у = sinx² непрерывна в точке х₀ = 0.

Решение. Функция z = x² непрерывна в точке х₀ = 0 как целая рациональная функция. Функция у = sinz непрерывна в точке z₀ = x₀² = 0, то по теореме 3 сложная функция у = sinz = sinx² непрерывна в точке х₀ = 0.

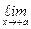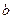Определение. Функция называется непрерывной на интеграле, если она непрерывна в каждой точке этого интервала. Если функция определена при х=и при этом f(x) = f(), то говорят, что f(x) в точке непрерывна справа. Аналогично, если f(x) =f(), то говорят, что f(x) в точке 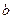непрерывна слева. Функция называется непрерывной на [], если она непрерывна в каждой его точке (в точке ─ непрерывна справа, в точке 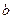─ непрерывна слева).

Функции, непрерывные на отрезке, обладают рядом важных свойств, которые выражаются следующими теоремами.

Теорема 4. (первая теорема Больцано-Коши).

Пусть функция f(x) непрерывна на [] и на концах отрезка имеет значения разных знаков. Тогда существует точка Î[], в которой f() = 0.

Теорема 5. (вторая теорема Больцано-Коши).

Пусть функция f(x) непрерывна на [], причём f()=A, f(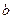)=B. Пусть С ─ любое число, заключённое между А и В. Тогда на отрезке [] найдётся точка такая, что f() = C.

Теорема 6. (первая теорема Вейерштрасса).

Если функция f(x) определена и непрерывна на [], то она ограничена на этом отрезке.

Теорема 7. (вторая теорема Вейерштрасса).

Если функция f(x) непрерывна на [], то она достигает на этом отрезке своего наименьшего значения и своего наибольшего значения, т.е. существуют такие точки х₁, х₂Î[], что для всех хÎ[] f(x₁) £ f(x) £ f (x₂).

Дата добавления: 2014-01-07