Основные теоремы дифференциального исчисления

Лекция 16.

Решение.

1) dy = (х⁴ − 3х² + 4)'dx = (4х³ – 6х)dx.

2) d²y = (4x³ – 6x)'(dx) = (12x² – 6)(dx)².

Основные теоремы дифференциального исчисления. Правило Лопиталя-Бернулли.

Теорема Ферма. Пусть функция f(x) определена () и в некоторой точке х₀ этого интервала имеет наибольшее или наименьшее значение. Тогда, если в точке х₀ существует производная, то она равна нулю, т.е. f ¢(x)=0.

Доказательство. Пусть для определённости в точке х₀ функция f(x) имеет наибольшее значение, т.е. для любого хÎ() выполняется неравенство f(x) £ f(x₀). Это означает, что ∆у = f(x₀+∆x) − f(x₀) £ 0 для любого приращения аргумента ∆х.

Возможны два случая:

1) ∆х > 0. Тогда 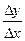£ 0 и, следовательно,

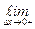
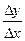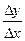= £ 0.

2) ∆х < 0. Тогда 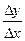³ 0 и, следовательно,

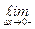
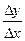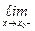
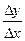= ³ 0.

По условию, f ¢(x) существует, поэтому существует 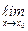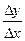. Но тогда существует односторонние пределы 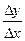и 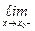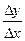, причём

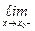
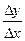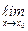
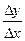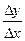0£ = = £ 0.

Всё это возможно только при 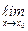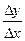= 0, т.е. при f ¢(x)=0.

Аналогично рассматривается случай, когда в точке х₀ функция f(x) имеет наименьшее значение.

Теорема Ролля. Пусть на [] определена функция f(x), причём: 1) f(x) непрерывна на []; 2) f(x) дифференцируема на (); 3) f() = f(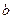). Тогда существует точка Î(), в которой f ¢() = 0.

Доказательство. Так как функция f(x) непрерывна на [], то по второй теореме Вейерштрасса она имеет на этом отрезке максимальное значение М и минимальное значение m, т.е. существуют такие точки х₁, х₂ Î[], в которых f(x₁) = m, f(x₂) = M и выполняются неравенства

m £ f(x) £ M

для всех хÎ[].

Возможны два случая:

1) M = m. Тогда f(x) = const = M = m. В этом случае для любого хÎ() имеем f '(x) = 0. Теорема верна.

2) m < M. Так как f() = f(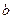), то хотя бы одно значение m или М достигается на (), т.е. существует Î() такая, что f() = m или f() = M. Поскольку f(x) дифференцируема в точке , то по теореме Ферма f '() = 0.

Теорема Лагранжа. Пусть на отрезке [] определена функция f(x), причём 1) f(x) непрерывна на []; 2) f(x) дифференцируема на (). Тогда существует точка Î() такая, что справедлива формула

.

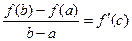Доказательство. Введём в рассмотрение на [] вспомогательную функцию

F(x) = f(x) −f() − 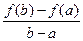×(x−).

Функция F(x) удовлетворяют всем трём условиям теоремы Ролля:

1) F(x) непрерывна на [] как разность двух непрерывных функций f(x) и линейной

функции

f() + 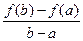×(x−);

2) F(x) дифференцируема на (). Действительно, f(x) дифференцируема на () по

условию, поэтому производная

F'(x) = f '(x) −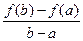

существует на ();

3) F() = 0; F(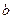) = 0, т.е. F() = F().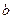

Тогда по теореме Ролля существует точка Î() такая, что F'() = 0, т.е.

f '() = .

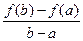Равенство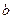 f()−f()=f '()()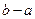 называется формулой Лагранжа или формулой конечных приращений.

Теорема Коши. Пусть функции f(x) и g(x) непрерывны на [] и дифференцируемы на (). Пусть, кроме того, g'(x)≠0. Тогда на () существует точка такая, что справедлива формула

(*)

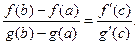Доказательство. Прежде всего отметим, что g(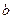) ≠ g(), т.е. формула (*) имеет смысл. Если предположить, что g(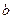) = g(), то по теореме Ролля для функции g(x) на () найдётся точка h такая, что g'(h) = 0. Это противоречит условию g'(x) ≠ 0 на ().

Рассмотрим на [] вспомогательную функцию

F'(x) = f '(x) − 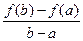×g'(x),

то

f '() − 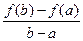×g'() = 0,

откуда, учитывая g'() ≠ 0, получим

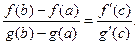
Формула (*) называется формулой Коши или обобщённой формулой конечных приращений.

Замечание. Если в формуле Коши взять функцию g(x) = x, то получим формулу Лагранжа

Снова вернёмся к вопросу раскрытия неопределённостей. Познакомимся с простым и эффективным методом раскрытия неопределённостей, который называется правилом Лопиталя-Бернулли. Основано это правило на следующей теореме.

Теорема Лопиталя-Бернулли. Пусть функции f(x) и g(x) определены и дифференцируемы на некотором интервале (), содержащем точку х₀, за исключением, быть может, самой точки х₀. Пусть, далее, 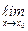f(x) = 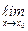g(x) = 0 и g'(x) ≠ 0 на (). Тогда, если существует 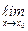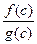, причём

=

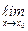
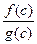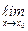
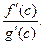
Пример 1. Найти .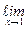

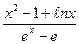Решение. Функции f(x)=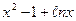и g(x)= 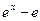определены дифференцируемы на (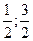), причём 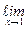f(x) = 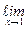g(x) = 0. Предел отношения производных этих функций существует:

=

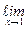
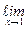
причём g'(x) = 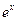≠ 0 для хÎ(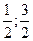). Теперь по теореме Лопиталя-Бернулли существует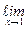 ­­­­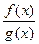_­, причём

==

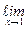
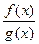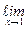
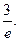
Дата добавления: 2014-01-07