Метод Ритца

Проекционные методы решения задач ОМД

Применение численных методов для анализа процессов и объектов ОМД

Задачи механики сплошных сред сводятся к дифференциальным уравнениям в частных производных, которые необходимо интегрировать при определенных краевых условиях [12, 13, 16, 17]. Приближенное решение краевых задач во многих случаях удается получить с применением так называемых прямых методов [29]. Прямыми называются методы приближенного решения задач теории дифференциальных и интегральных уравнений, которые сводят эти задачи к конечным системам алгебраических уравнений. В теории и практике применения прямых методов особое место занимают два метода: метод Ритца и метод Галеркина.

В первом из них задача интегрирования дифференциального уравнения заменяется некоторой равносильной вариационной задачей. Второй основан на ортогонализации невязки операторного уравнения по отношению к координатной системе функций и, вообще говоря, не связан с какой либо вариационной задачей.

Достаточно подробно данные методы и применение их для решения задач ОМД рассмотрены в работах [13, 15, 16, 17, 29].

Пусть требуется найти минимум некоторого функционала J(x) с областью определения D_J.

Выберем координатную систему функций φ₁, φ₂, …, φ_n, удовлетворяющую следующим требованиям [29]:

1) элементы координатной системы, взятые в любом конечном количестве, линейно независимы;

2) координатная система полна в некоторой метрике, определенной на области D_J;

3) при любых значениях постоянных а₁, а₂,…, а_n элемент

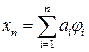(4.1)

принадлежит D_J и выражение J(x_n) имеет смысл.

Рассматривая его как функцию конечного числа переменных а₁, а₂,…, а_n, найдем те значения, при которых J(x_n) достигает минимума. С этой целью необходимо решить следующую систему уравнений

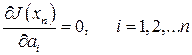(4.2)

(необходимое условие экстремума J(x_n)). Убедившись, что найденные значения постоянных а_i действительно реализуют минимум величины J, подставим эти значения в выражение (4.1). В результате получим элемент x_n, который назовем n –м приближением по Ритцу решения данной вариационной задачи.

Для неоднородных граничных условий можно искать n –е приближение по Ритцу в следующем виде

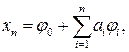(4.3)

где элемент φ₀ удовлетворяет заданным граничным условиям, а φ_i удовлетворяет соответствующим однородным граничным условиям.

Решение системы уравнений (4.2) является в общем случае весьма сложной задачей. Она существенно упрощается, если J(x_n) – квадратичный функционал, в этом случае уравнения (4.2) линейны относительно а_i.

На практике во многих случаях приходится ограничиваться сравнительно небольшим числом членов рядов (4.1) и (4.2), поэтому удачный выбор координатных функций имеет решающее значение. При решении вариационных задач обработки металлов давлением для выбора координатных функций обычно используют результаты экспериментальных исследований.

Пример. Рассмотрим расчет деформированного состояния полосы прямоугольного сечения при кузнечной протяжке (рис. 2.9) при указанных там граничных условиях. Модель построим для поперечного сечения yOz.

Кривую упрочнения Т(Н) аппроксимируем следующей функцией [16]

Т = 1,88 Н ^1/3.

Эта зависимость соответствует деформации стали марки 45 при 1100⁰С.

Функционал для рассматриваемого случая

(4.4)

где

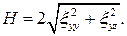
Подходящей последовательностью функций вида (4.1) для поля скоростей, удовлетворяющей граничным условиям, будет

(4.5)

Ограничим (4.5) двумя членами ряда. Второй компонент скорости найдем из условия несжимаемост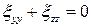и при

Очевидно, что из выражения (4.5) следует

После интегрирования данного выражения для нахождения и преобразований получили компоненты тензора скорости деформации [16]

(4.6а)

(4.6б)

Деформированное состояние описывается приближенно формулами (4.6), которые содержат один варьируемый коэффициент а₁, который определим из условия экстремума функционала (4.4)

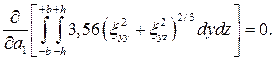
В результате найдено а₁ =0,73 v, подставив которое в (4.6) получим

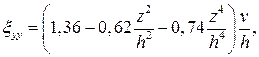
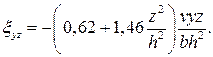
Распределение интенсивности скоростей деформации в безразмерном виде Н¹ = Н/(2v/h) для одной четверти представлено на рис. 4.1 (подготовлено с применением пакета EXCEL).

Шкала H¹

z/h

y/b

H¹

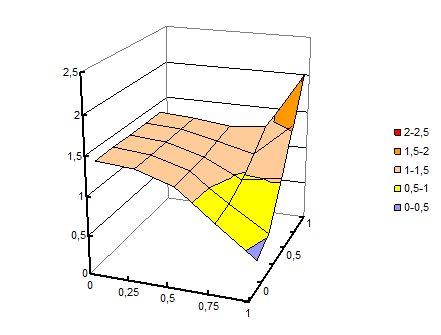
Рис. 4.1. Распределение интенсивностей скорости деформации

по сечению заготовки при протяжке

Дата добавления: 2014-01-07