
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Выпуклые множества и выпуклые функции. Свойства выпуклых функций
|
|
|
|
Определение 1:
Пусть x,yЄЕn. Множество {z}ЄЕn точек
вида z= x+(1-
x+(1- )y,
)y,  Є[0,1] (1)
Є[0,1] (1)
называется отрезком, соединяющим точки x и y.
В пространстве Еn, n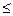 3 соотношение (1) определяет обычный отрезок, соединяющий точки х и у. Для
3 соотношение (1) определяет обычный отрезок, соединяющий точки х и у. Для 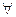 точки z, прямой, проходящей через точки х и у, справедливо представление: z=y+
точки z, прямой, проходящей через точки х и у, справедливо представление: z=y+ (x-y), которое отличается от (1) лишь формой записи. При
(x-y), которое отличается от (1) лишь формой записи. При  =0 точки z совпадает с одним из концов отрезка (z=y), а при
=0 точки z совпадает с одним из концов отрезка (z=y), а при  =1 с другим (z=x). При изменении
=1 с другим (z=x). При изменении  от 0 до 1 точка z пробегает отрезок от точки у до точки х.
от 0 до 1 точка z пробегает отрезок от точки у до точки х.
Определение 2:
Множество UЄEn называется вынужденным, если вместе с любыми точками ХиY Є U оно содержит и весь отрезок (1).
Очевидно, Еn – выпуклое множество.
Теорема 1: Пересечение выпуклых множествU , i=1,…,m, есть выпуклое множество, если оно содержит более одной точки.
, i=1,…,m, есть выпуклое множество, если оно содержит более одной точки.
Определение 3:
f(x), заданная на выпуклом множестве UЄEn, называется выпуклой, если для 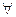 точек ХиYЄU и
точек ХиYЄU и 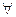
 Є[0,1] выполняется неравенство:
Є[0,1] выполняется неравенство:
f[ х+(1-
х+(1- )у]
)у]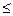
 f(x)+(1-
f(x)+(1- )f(y) (2)
)f(y) (2)
Функция f(x) называется строго выпуклой, если для всех  Є(0,1) неравенство (2) выполняется как строгое.
Є(0,1) неравенство (2) выполняется как строгое.
Теорема 2: Линейная комбинация выпуклых на выпуклом множестве U функций f (x), i=
(x), i=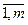 с неотрицательными коэффициентами
с неотрицательными коэффициентами 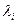 , т.е. f(x)=
, т.е. f(x)=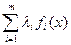 ,
, 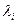
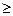 , есть выпуклая на множестве U функция.
, есть выпуклая на множестве U функция.
Теорема 3: Пусть g(х) – выпуклая функция, заданная в пространстве Еn. Тогда множество U точек Х, удовлетворяющих неравенству g(х)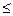 в, выпукло.
в, выпукло.
Приведем свойства выпуклых функций, играющие важную роль в вопросах min-ии:
Теорема 1: Пусть f(x) – выпуклая на выпуклом множестве U функция. Тогда любой ее локальный минимум на множестве U является одновременно и глобальным.
Теорема 2: Глобальный min-м строго выпуклой функции f(x) на выпуклом множестве U может достигаться в единственной точке.
|
|
|
Наличие локальных min-ов функции f(x), не совпадающих с глобальным, сильно затрудняет поиск точки глобального min-ма f(x). Поэтому применение многих методов min-ции обосновано только для функции, не имеющих точек локального min-ма, отличных от глобального. Этим объясняется особая роль свойства выпуклости функции во многих вопросах оптимизации.
Замечание: Отметим, что не всякая выпуклая в Еn функция достигает min-го значения, даже если она ограничена снизу.
Введем класс функций, для которых min-м в Еn обязательно существует.
Определение:
Функция f(x), заданная в Еn, называется сильно выпуклой, если существует такое число 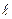 >0 (
>0 (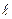 - это константа сильной выпуклости), что для всех ХиYЄЕn и любого
- это константа сильной выпуклости), что для всех ХиYЄЕn и любого  Є[0,1] выполняется неравенство:
Є[0,1] выполняется неравенство:
f[ x+(1-
x+(1- )y]
)y]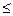
 f(x)+(1-
f(x)+(1- )f(y)-
)f(y)- (1-
(1- )
)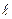 ||x-y||
||x-y||
Очевидно, сильно выпуклая функция является выпуклой и строго выпуклой.
Замечание: Можно показать, что у сильно выпуклой функции точка глобального min-ма существует и единственна.
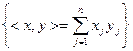 - скалярное произведение
- скалярное произведение
Для дифференцированных в Еn функций f(x) выпуклость эквивалентна выполнению неравенства
f(x)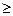 f(x
f(x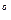 ), x-x
), x-x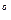 >, (1) – нестрогая выпуклость
>, (1) – нестрогая выпуклость
f(x)>f(x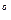 )+<f
)+<f (х
(х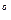 ), x-x
), x-x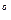 >, (2) – строгая выпуклость
>, (2) – строгая выпуклость
f(x)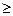 f(x
f(x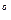 )+<f
)+<f (х
(х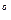 ), x-x
), x-x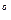 >+
>+ ||x-х
||x-х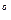 ||
|| (3) – сильная выпуклость
(3) – сильная выпуклость
для любых x,x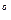 ЄЕn.
ЄЕn.
Рассмотрим графики этих функций:
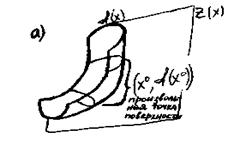
а) График функции f(x) не ниже касательной плоскости z=f(x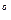 )+<f
)+<f (х
(х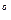 ), x-x
), x-x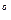 >, проходящей через произвольную точку поверхности (x
>, проходящей через произвольную точку поверхности (x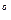 ,f(x
,f(x ))
))
|
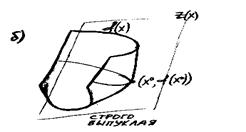
б) График функции имеет единственную общую точку с плоскостью z
|
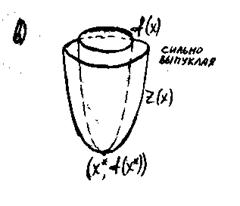
в) Предположим, что f(x) сильно выпуклая и Х* - точка ее глобального min-а. Тогда f (х*)=0 и неравенство (3) принимает вид f(x)
(х*)=0 и неравенство (3) принимает вид f(x)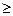 f(x*)+
f(x*)+ ||x-х*||
||x-х*||
Поверхность z= f(x*)+ ||x-х*||
||x-х*|| представляет собой параболоид вращения с вершиной в точке (x*, f(x*)). Поэтому график сильно выпуклой функции расположен внутри некоторого параболоида вращения.
представляет собой параболоид вращения с вершиной в точке (x*, f(x*)). Поэтому график сильно выпуклой функции расположен внутри некоторого параболоида вращения.
|
Замечание:
Из неравенства (1) для выпуклой дифференциальной функции f(х) следует, что условие f (х*)=0 является не только необходимым, но и достаточным для того, чтобы х* была точкой глобального min-ма функции f(х).
(х*)=0 является не только необходимым, но и достаточным для того, чтобы х* была точкой глобального min-ма функции f(х).
|
|
|
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2228; Нарушение авторских прав?; Мы поможем в написании вашей работы!