
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод Ньютона
|
|
|
|
Пусть функция f(x) дважды дифференцируема в Еп. Тогда для нее можно записать разложение по формуле Тейлора в окрестности точки х :
:
f(x)=f(x )+<f
)+<f (x
(x ), x-x
), x-x >+1/2<f"(x
>+1/2<f"(x )(x-x
)(x-x ), x-x
), x-x >+0(||x-x
>+0(||x-x ||
|| )
)
Отсюда видно, что поведение функции f(x) с точностью до величины порядка 0(||х-x ||
|| ) может быть описано квадратичной функцией
) может быть описано квадратичной функцией
Ф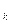 (k)=1/2<f"(x
(k)=1/2<f"(x )(x-x
)(x-x ), x-x
), x-x >+<f
>+<f (x
(x ), x-x
), x-x >+f(x
>+f(x ) (1)
) (1)
Минимизируем функцию Ф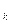 (k) вместо f(x). Найдем ее точку минимума x
(k) вместо f(x). Найдем ее точку минимума x из условия Ф
из условия Ф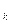 '(х)=0:
'(х)=0:
Ф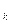 '(х)=f"(x
'(х)=f"(x )(x-x
)(x-x )+f
)+f (x
(x )=0 (2)
)=0 (2)
Пусть матрица Гессе f"(х) положительно определена при всех хЄ Еп и, следовательно, невырождена (det f "(х)>0). Тогда существует обратная матрица [f"(х)]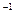 . Отметим, что квадратичная функция (1) с положительно определенной матрицей f"(x
. Отметим, что квадратичная функция (1) с положительно определенной матрицей f"(x ) сильно выпукла и уравнение (2) определяет единственную точку глобального минимума функции Ф
) сильно выпукла и уравнение (2) определяет единственную точку глобального минимума функции Ф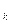 (x). Умножим слева обе части равенства (2) на матрицу [f"(х)]
(x). Умножим слева обе части равенства (2) на матрицу [f"(х)]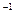 и найдем точку минимума x
и найдем точку минимума x квадратичной функции (1), аппроксимирующей f(x) в окрестности точки х=x
квадратичной функции (1), аппроксимирующей f(x) в окрестности точки х=x :
:
x =x
=x -[f"(х)]
-[f"(х)]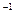 f
f (x
(x ), k=0,1,… (3)
), k=0,1,… (3)
Итерационный процесс (3), начатый из произвольной точки x Є Еп, называется методом Ньютона минимизации функции многих переменных и является обобщением метода Ньютона в одномерном случае.
Є Еп, называется методом Ньютона минимизации функции многих переменных и является обобщением метода Ньютона в одномерном случае.
Очевидно, для квадратичной функции с положительно определенной матрицей А применение метода Ньютона обеспечивает получение точки глобального минимума ровно за один шаг из любой точки x Є Еп.
Є Еп.
Для выпуклой функции, отличной от квадратичной, применение этого метода обеспечивает, как правило, быструю сходимость. Дело в том, что на каждом шаге итерационного процесса (3) используется информация о поведении функции f(x) в окрестности точки x , содержащаяся не только в значениях первых, но и вторых ее частных производных. Поэтому при прочих равных условиях следует ожидать более быструю сходимость метода Ньютона по сравнению с градиентными методами.
, содержащаяся не только в значениях первых, но и вторых ее частных производных. Поэтому при прочих равных условиях следует ожидать более быструю сходимость метода Ньютона по сравнению с градиентными методами.
|
|
|
При выборе достаточно хорошего начального приближения x Є Еп минимизирующая последовательность {x
Є Еп минимизирующая последовательность {x } для сильно выпуклой дважды дифференцируемой функцииm f(х) сходится к точке минимума с квадратичной скоростью р(x
} для сильно выпуклой дважды дифференцируемой функцииm f(х) сходится к точке минимума с квадратичной скоростью р(x , х*)<=сq
, х*)<=сq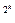 , qЄ(0;1). Если же точка х0 выбрана недостаточно близкой к точке х*, то последовательность (3) может расходиться.
, qЄ(0;1). Если же точка х0 выбрана недостаточно близкой к точке х*, то последовательность (3) может расходиться.
Отметим, что даже сходящаяся последовательность {x } метода Ньютона не всегда обеспечивает монотонное убывание f(х), т.е. неравенство f(x
} метода Ньютона не всегда обеспечивает монотонное убывание f(х), т.е. неравенство f(x )<f(x
)<f(x ) для некоторых k = 0,1,... может нарушаться. Этот недостаток устранен в обобщенном методе Ньютона:
) для некоторых k = 0,1,... может нарушаться. Этот недостаток устранен в обобщенном методе Ньютона:
x =x
=x -α
-α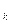 [f"(x
[f"(x )]
)]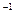 f
f (x
(x ),
),
где величина α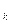 >0 находится на каждом шаге из условия исчерпывающего спуска по направлению р
>0 находится на каждом шаге из условия исчерпывающего спуска по направлению р =-[f"(x
=-[f"(x )]
)]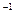 f
f (x
(x ).
).
Недостатком метода Ньютона является необходимость вычисления и обращения матрицы Гессе на каждой итерации.
Пример 3.13. Найти точку минимума функции f(x)=4x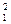 +3x
+3x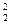 -4x
-4x x
x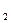 +x
+x методом Ньютона из начальной точки х
методом Ньютона из начальной точки х =(0,0).
=(0,0).
Градиент f (х°)=(-1,0), матрица Гессе f"(х°)=A=
(х°)=(-1,0), матрица Гессе f"(х°)=A=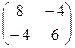 . Найдем обратную матрицу [f"(х°)]
. Найдем обратную матрицу [f"(х°)]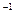 =
= . С помощью формулы (3) получаем х
. С помощью формулы (3) получаем х =х°-α
=х°-α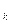 [f"(х°)]
[f"(х°)]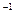 f
f (х°)=(-3/16, -1/8). Так как f
(х°)=(-3/16, -1/8). Так как f (х
(х )= (0,0), то задача решена: х*=х
)= (0,0), то задача решена: х*=х . Целевая функция квадратична, поэтому решение задачи получено за одну итерацию.
. Целевая функция квадратична, поэтому решение задачи получено за одну итерацию.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 194; Нарушение авторских прав?; Мы поможем в написании вашей работы!