Частично-рекурсивные функции

Большинство арифметических и логических функций являются примитивно–рекурсивными. Однако класс примитивно–рекурсивных функций не охватывает всех вычислимых в интуитивном смысле функций. Для построения остальных функций используется так называемый оператор минимизации (m –оператор, оператор наименьшего корня). Оператор минимизации определяет новую арифметическую функцию 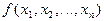от n переменных с помощью ранее построенной арифметической функции 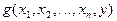от n+1 переменных.

Зафиксируем набор значений аргументов 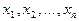и рассмотрим уравнение относительно y: .

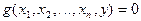Наименьшее целое неотрицательное значение 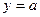, удовлетворяющее этому уравнению, обозначим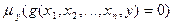

Говорят, что функция 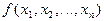получена из функции 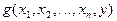операцией минимизации, если

.

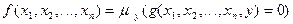Процесс вычисления осуществляется последовательным перебором значений 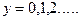и подстановкой их в уравнение 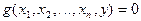до тех пор, пока не выполнится 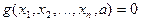, либо бесконечно. Оператор минимизации работает бесконечно в одном из следующих случаев.

1. Значение 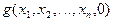не определено.

2. Значение 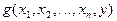для 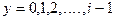определены, но не равны нулю, а значение 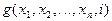не определено.

3. Значение 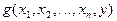определены для всех 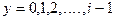, но не равны нулю

Алгоритм работы оператора минимизации показан в виде блок-схемы на рис 2.2. Для простоты на блок схеме принято n=1.

Оператор минимизации является удобным средством получения обратных функций: вычитание, деление, извлечение корня и др.

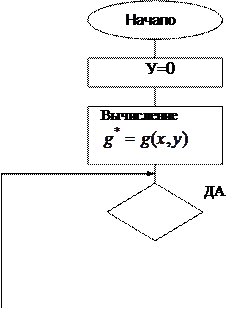
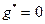
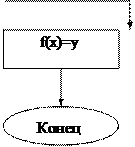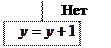Рис 2.2. Алгоритм работы оператора минимизации

Пример 13. Определение операции «вычитание»:

.

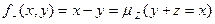При x=5;y=2 z принимает значения 0,1,2,3,4.... Значение z=3 является искомым.

При x=4;y=6 z принимает значения 0,1,2,3,4..., ни одно из них не удовлетворяет уравнению 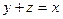, оператор минимизации при этом работает бесконечно, следовательно значение 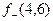не определено.

Определение частично-рекурсивной функции.

Функция называется частично-рекурсивной, если она может быть построена из простейших с помощью конечного числа применений оператора суперпозиции, примитивной рекурсии и минимизации.

Частично-рекурсивная функция является не всюду определенной, причем там, где она не определена, процесс ее вычисления продолжается бесконечно.

Частично-рекурсивная функция является общерекурсивной, если она всюду определена.

Класс частично-рекурсивных функций шире класса общерекурсивных функций, который, в свою очередь шире класса примитивно-рекурсивных функций.

Связь между алгоритмами и рекурсивными функциями выражается тезисом Черча:

какова бы ни была вычислимая неотрицательная целочисленная функция от неотрицательных целочисленных аргументов, существует тождественно равная ей частично-рекурсивная функция.

Поскольку вычислимая функция – это функция, для вычисления которой существует алгоритм, тезис Черча выражает эквивалентность алгоритмов и частично-рекурсивных функций.

Тезис Черча доказать нельзя, т.к. понятия «алгоритм» и «вычислимая функция» являются интуитивными, а не строго математическими.

Лекция 3. МАШИНЫ ТЬЮРИНГА

Рекурсивные функции представляют алгоритм через вычислимую функцию, т.е. понятие «вычислимая функция» является первичным по отношению к понятию «алгоритм». Машины Тьюринга (МТ) являются в этом смысле более естественными, т.к. вначале уточняют понятие «алгоритм», а через него – вычислимую функцию.

Машина Тьюринга (Тьюринга-Поста, т.к. предложена ими почти одновременно и независимо в 1936-1937 гг.) построена на основе использования свойства детерминированности алгоритмов. Основной смысл этого свойства сводится к тому, что алгоритмический процесс должен выполнятся механически, т.е. может быть реализован машиной. Машина Тьюринга является абстрактной, т.к. имеет неограниченные ресурсы, что требуется для реализации любых алгоритмов.

В данной теме вводятся некоторые понятия символьных конструкций и операций над ними, описаны функционирование и способы задания МТ, способы композиции МТ, позволяющие строить сложные МТ из более простых, приводится понятие об эквивалентности МТ и рекурсивных функций.

Наиболее полно (в рамках программы курса) машины Тьюринга описаны в [ 1,4,8 ], приводится большое количество примеров. В [ 2 ] изложение более популярное и менее формализованное. Дополнительный материал о МТ можно найти в [ 7 ].

Дата добавления: 2014-01-07