Пусть имеется функция

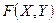
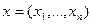
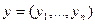
Определение: Точка 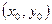, где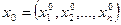

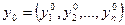
называется седловой точкой функции 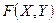, если для всех 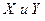выполняется условие:

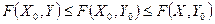
причем в самой седловой точке значение функции 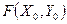равно:

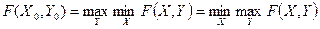
Пример:

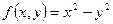(гиперболический параболоид)

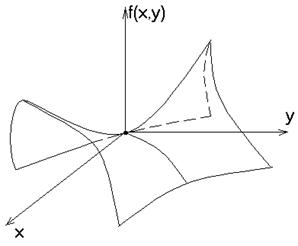Точка 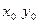является седловой точкой этой функции.

Теорема: Пусть 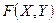- дифференцируемая функция, тогда для того, чтобы точка 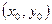была седловой точкой этой функции в области 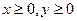необходимо выполнение условий:

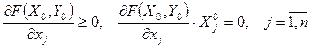
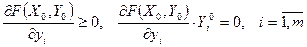
Это дифференциальный аналог седловой точки.

Теорема Куна-Таккера:

Пусть задача нелинейного программирования имеет вид:

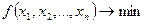
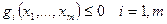(3)

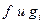-дифференцируемые и выпуклые по x.

Составим функцию Лагранжа:

Введем множители Лагранжа

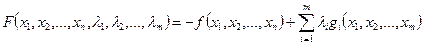(4)

Сама Теорема:

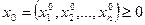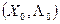Вектор оптимальным решением (3) тогда и только тогда, когда существует такой вектор такой что точка является седловой точкой функции Лагранжа (4), т.е. выполняется условие:

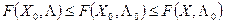
Аналитическое выражение условия теоремы:

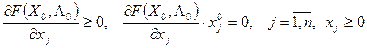
(5)

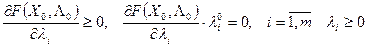
Для задачи вогнутого нелинейного программирования:

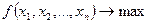
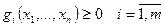(6)

Условия Куна – Таккера будут иметь вид:

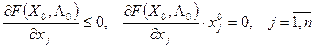
(7)

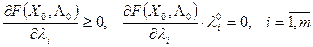
Сформулированная теорема Куна – Таккера позволяет находить решение задачи нелинейного программирования с помощью отыскания седловой точки функции Лагранжа.

Алгоритм решения задачи вогнутого (выпуклого) нелинейного программирования с помощью теоремы Куна – Таккера:

1. По исходной задаче нелинейного программирования составляется функция Лагранжа .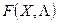

2. Записывается условие для седловой точки функции Лагранжа. Либо (5), либо (7). В результате получаем систему уравнений или неравенств.

3. Находится совместное решение системы уравнений и неравенств, полученных на втором шаге. В результате вычисляется оптимальное решение.

Квадратичное программирование

Квадратичное программирование – это класс задач нелинейного программирования у которых целевая функция 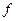представляет сумму линейной и квадратичной функции, а все ограничения линейны.

В общем случае задача квадратичного программирования имеет постановку:

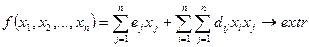
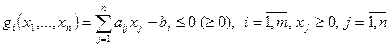(1)

Задачу квадратичного программирования удобнее записывать в матричной форме:

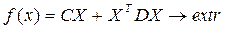
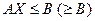
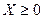
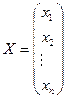
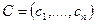
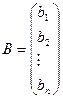
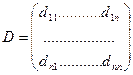
D – квадратичная матрица, причем симметрична относительно главной диагонали.

Для решения задачи (1) или (2) применяется условие, сформулированное в теореме Куна – Таккера, т.к. задача квадратичного программирования относится к задаче вогнутого (выпуклого) нелинейного программирования, поскольку функция f – выпуклая (вогнутая), а ограничения выпуклые.

Вопрос о том, будет ли выпуклая или вогнутая функция f зависит от того, вогнута или выпукла квадратичная функция: 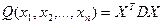.,поскольку линейная функция CX является и выпуклой и вогнутой одновременно. Является ли функция Q вогнутой или выпуклой, определяется тем, является ли она положительно - определенной, положительно - полуопределенной, отрицательно - определенной, отрицательно полуопределенной, или неопределенной.

Определение: Функция Q называется отрицательно – определенной, если она строго меньше 0 для всех 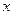, кроме .

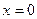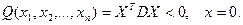
Пример: 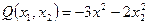при любых 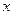она ‘<’ 0 и при 0 она ‘=’ 0.

Определение: Функция Q называется отрицательно – полуопределенной, если она меньше либо равна 0 для всех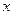, кроме 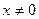, для которого она ‘=’ 0.

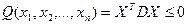
Определение: Квадратичная форма называется положительно – определенной (положительно – полуопределенной), если квадратичная форма:

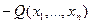отрицательно – определенная или отрицательно – полуопределенная.

Определение: Квадратичная форма называется неопределенной, если она отрицательна для одних значений 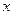и положительна для других.

Признаки, позволяющие определить, к какому из перечисленных видов относится квадратичная форма.

Составим определители:

,....

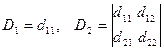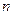- определителей.

1. Если все определители 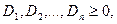то квадратичная форма положительно – определенная.

2. Если в ряду чисел 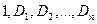знаки строго чередуются, то квадратичная форма отрицательно – определенная.

3. Если ранг матрицы 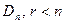, то квадратичная форма будет положительно - полуопределенная, если первые r определители положительны, а остальные равны 0.

4. Если 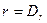, причем 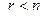и в ряду чисел 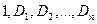знаки чередуются, а остальные определители 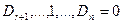, то квадратичная форма отрицательно – определенная.

5. Если в ряду чисел нет строгого чередования, то квадратичная форма неопределенная.

Квадратичная форма строго вогнута, если она отрицательно – определенная. Вогнута, если отрицательно – полуопределенная. Строго выпуклая, если положительно - определенная, выпуклая – положительно - полуопределенная.

Дата добавления: 2014-01-07