Тема 7. Ряды распределения

7.1.Ряды распределения и их построение

Важнейшей частью статистического анализа является построение рядов распределения (структурной группировки) с целью выделения характерных свойств и закономерностей изучаемой совокупности. В зависимости от того, какой признак (количественный или качественный) взят за основу группировки данных, различают соответственно типы рядов распределения.

Если за основу группировки взят качественный признак, то такой ряд распределения называют атрибутивным (распределение по видам труда, по полу, по профессии, по религиозному признаку, национальной принадлежности и т.д.).

Если ряд распределения построен по количественному признаку, то такой ряд называют вариационным. Построить вариационный ряд - значит упорядочить количественное распределение единиц совокупности по значениям признака, а затем подсчитать числа единиц совокупности с этими значениями (построить групповую таблицу).

Выделяют три формы вариационного ряда: ранжированный ряд, дискретный ряд и интервальный ряд.

Ранжированный ряд - это распределение отдельных единиц совокупности в порядке возрастания или убывания исследуемого признака. Ранжирование позволяет легко разделить количественные данные по группам, сразу обнаружить наименьшее и наибольшее значения признака, выделить значения, которые чаще всего повторяются.

Другие формы вариационного ряда - групповые таблицы, составленные по характеру вариации значений изучаемого признака. По характеру вариации различают дискретные (прерывные) и непрерывные признаки.

Дискретный ряд - это такой вариационный ряд, в основу построения которого положены признаки с прерывным изменением (дискретные признаки). К последним можно отнести тарифный разряд, количество детей в семье, число работников на предприятии и т.д. Эти признаки могут принимать только конечное число определенных значений.

Дискретный вариационный ряд представляет таблицу, которая состоит из двух граф. В первой графе указывается конкретное значение признака, а во второй - число единиц совокупности с определенным значением признака.

Если признак имеет непрерывное изменение (размер дохода, стаж работы, стоимость основных фондов предприятия и т.д., которые в определенных границах могут принимать любые значения), то для этого признака нужно строить интервальный вариационный ряд.

Групповая таблица здесь также имеет две графы. В первой указывается значение признака в интервале «от - до» (варианты), во второй - число единиц, входящих в интервал (частота).

Частота (частота повторения) - число повторений отдельного варианта значений признака, обозначается f_i, а сумма частот, равная объему исследуемой совокупности, обозначается

где k - число вариантов значений признака

Очень часто таблица дополняется графой, в которой подсчитываются накопленные частоты S, которые показывают, какое количество единиц совокупности имеет значение признака не большее, чем данное значение.

Частоты ряда f могут заменяться частостями w, выраженными в относительных числах (долях или процентах). Они представляют собой отношения частот каждого интервала к их общей сумме, т.е.:

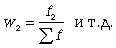(7.1)

При построении вариационного ряда с интервальными значениями прежде всего необходимо установить величину интервала i, которая определяется как отношение размаха вариации R к числу групп m:

(7.2)

где R = x_max - x_min; m = 1 + 3,322 lgn (формула Стерджесса); n - общее число единиц совокупности.

7.2.

Медиана и мода - структурные (распределительные) средние величины

Для определения структуры совокупности используют особые средние показатели, к которым относятся медиана и мода, или так называемые структурные средние. Если средняя арифметическая рассчитывается на основе использования всех вариантов значений признака, то медиана и мода характеризуют величину того варианта, который занимает определенное среднее положение в ранжированном вариационном ряду.

Медиана (Ме) - это величина, которая соответствует варианту, находящемуся в середине ранжированного ряда.

Для ранжированного ряда с нечетным числом индивидуальных величин (например, 1, 2, 3, 3, 6, 7, 9, 9, 10) медианой будет величина, которая расположена в центре ряда, т.е. пятая величина.

Для ранжированного ряда с четным числом индивидуальных величин (например, 1, 5, 7, 10, 11, 14) медианой будет средняя арифметическая величина, которая рассчитывается из двух смежных величин. Для нашего случая медиана равна (7+10): 2= 8,5.

То есть для нахождения медианы сначала необходимо определить ее порядковый номер (ее положение в ранжированном ряду) по формуле

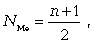(7.3)

где n - число единиц в совокупности.

Численное значение медианы определяют по накопленным частотам в дискретном вариационном ряду. Для этого сначала следует указать интервал нахождения медианы в интервальном ряду распределения. Медианным называют первый интервал, где сумма накопленных частот превышает половину наблюдений от общего числа всех наблюдений.

Численное значение медианы обычно определяют по формуле

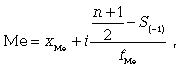(7.4)

где x_Ме - нижняя граница медианного интервала; i - величина интервала; S_-1 - накопленная частота интервала, которая предшествует медианному; f - частота медианного интервала.

Модой (Мо) называют значение признака, которое встречается наиболее часто у единиц совокупности. Для дискретного ряда модой будет являться вариант с наибольшей частотой. Для определения моды интервального ряда сначала определяют модальный интервал (интервал, имеющий наибольшую частоту). Затем в пределах этого интервала находят то значение признака, которое может являться модой.

Чтобы найти конкретное значение моды, необходимо использовать формулу

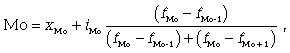(7.5)

где x_Мо - нижняя граница модального интервала; i_Мо - величина модального интервала; f_Мо - частота модального интервала; f_Мо-1 - частота интервала, предшествующего модальному; f_Мо+1 - частота интервала, следующего за модальным.

Мода имеет широкое распространение в маркетинговой деятельности при изучении покупательского спроса, особенно при определении пользующихся наибольшим спросом размеров одежды и обуви, при регулировании ценовой политики.

7.3.Кривые распределения и критерии согласия

Основной целью анализа вариационных рядов является выявление закономерности распределения, исключая при этом влияние случайных для данного распределения факторов. Этого можно достичь, если увеличивать объем исследуемой совокупности и одновременно уменьшать интервал ряда. При попытке изображения этих данных графически мы получим некоторую плавную кривую линию, которая для полигона частот будет являться некоторым пределом. Эту линию называют кривой распределения.

Иными словами, кривая распределения есть графическое изображение в виде непрерывной линии изменения частот в вариационном ряду, которое функционально связано с изменением вариант. Кривая распределения отражает закономерность изменения частот при отсутствии случайных факторов. Графическое изображение облегчает анализ рядов распределения [Литература: 2. C. 115-119, 138-144].

Известно достаточно много форм кривых распределения, по которым может выравниваться вариационный ряд, но в практике статистических исследований наиболее часто используются такие формы, как нормальное распределение и распределение Пуассона.

Нормальное распределение зависит от двух параметров: средней арифметической и среднего квадратического отклонения 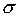. Его кривая выражается уравнением

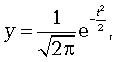(7.6)

где у - ордината кривой нормального распределения; 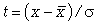- стандартизованные отклонения; е и π - математические постоянные; x - варианты вариационного ряда; - их средняя величина; 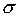- cреднее квадратическое отклонение.

Если нужно получить теоретические частоты f' при выравнивании вариационного ряда по кривой нормального распределения, то можно воспользоваться формулой

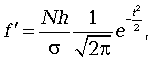(7.7)

где 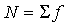- сумма всех эмпирических частот вариационного ряда; h - величина интервала в группах; 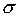- cреднее квадратическое отклонение; 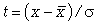- нормированное отклонение вариантов от средней арифметической; все остальные величины легко вычисляются по специальным таблицам.

При помощи этой формулы мы получаем теоретическое (вероятностное) распределение, заменяя им эмпирическое (фактическое) распределение, по характеру они не должны отличаться друг от друга.

Тем не менее в ряде случаев, если вариационный ряд представляет собой распределение по дискретному признаку, где при увеличении значений признака х частоты начинают резко уменьшаться, а средняя арифметическая, в свою очередь, равна или близка по значению к дисперсии (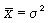), такой ряд выравнивается по кривой Пуассона [Литература: 5. С. 45].

Кривую Пуассона можно выразить отношением

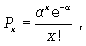(7.8)

где P_x - вероятность наступления отдельных значений х; 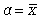- средняя арифметическая ряда.

При выравнивании эмпирических данных теоретические частоты можно определить по формуле

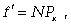(7.9)

где f' - теоретические частоты; N - общее число единиц ряда.

Сравнивая полученные величины теоретических частот f' c эмпирическими (фактическими) частотами f, убеждаемся, что их расхождения могут быть весьма невелики.

Объективная характеристика соответствия теоретических и эмпирических частот может быть получена при помощи специальных статистических показателей, которые называют критериями согласия.

Для оценки близости эмпирических и теоретических частот применяются критерий согласия Пирсона, критерий согласия Романовского, критерий согласия Колмогорова.

Наиболее распространенным является критерий согласия К. Пирсона 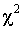, который можно представить как сумму отношений квадратов расхождений между f' и f к теоретическим частотам:

(7.10)

Вычисленное значение критерия 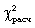необходимо сравнить с табличным (критическим) значением . Табличное значение определяется по специальной таблице, оно зависит от принятой вероятности Р и числа степеней свободы k (при этом k = m - 3, где m - число групп в ряду распределения для нормального распределения). При расчете критерия согласия Пирсона должно соблюдаться следующее условие: достаточно большим должно быть число наблюдений (n 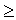50), при этом если в некоторых интервалах теоретические частоты < 5, то интервалы объединяют для условия > 5.

Если 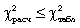, то расхождения между эмпирическими и теоретическими частотами распределения могут быть случайными и предположение о близости эмпирического распределения к нормальному не может быть отвергнуто.

В том случае, если отсутствуют таблицы для оценки случайности расхождения теоретических и эмпирических частот, можно использовать критерий согласия В.И. Романовского К_Ром, который, используя величину 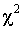, предложил оценивать близость эмпирического распределения кривой нормального распределения при помощи отношения

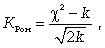(7.11)

где m - число групп; k = (m - 3) - число степеней свободы при исчислении частот нормального распределения.

Если вышеуказанное отношение < 3, то расхождения эмпирических и теоретических частот можно считать случайными, а эмпирическое распределение - соответствующим нормальному. Если отношение > 3, то расхождения могут быть достаточно существенными и гипотезу о нормальном распределении следует отвергнуть.

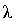Критерий согласия А.Н. Колмогорова используется при определении максимального расхождения между частотами эмпирического и теоретического распределения, вычисляется по формуле

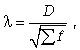(7.12)

где D - максимальное значение разности между накопленными эмпирическими и теоретическими частотами; 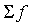- сумма эмпирических частот.

По таблицам значений вероятностей 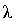-критерия можно найти величину 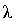, соответствующую вероятности Р. Если величина вероятности Р значительна по отношению к найденной величине 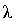, то можно предположить, что расхождения между теоретическим и эмпирическим распределениями несущественны.

Необходимым условием при использовании критерия согласия Колмогорова является достаточно большое число наблюдений (не меньше ста).

Вопросы для самоконтроля к теме 7

Дата добавления: 2014-01-07