С близкими частотами

СЛОЖЕНИЕ ДВУХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ ОДНОГО НАПРАВЛЕНИЯ

Если амплитуды складываемых гармонических колебаний одинакового направления равны, а их частоты мало отличаются друг от друга, т.е. , то при их сложении получаются колебания с периодически изменяющейся амплитудой. Такие колебания называются биениями.

Сложив колебания с близкими частотами, для которых равны:

- их амплитуды а₁= а₂;

- начальные фазы ,

получим уравнение биений:

, где (3.14)

- амплитуда результирующего колебания, т.е. биений; - фаза биений.

Амплитуду биений найдем, воспользовавшись векторной диаграммой по теореме косинусов:

, где 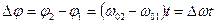, следовательно,

и окончательно получаем:

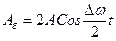. (3.15)

Таким образом, амплитуда биений изменятся со временем в пределах от до нуля с циклической частотой 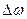. Период биений и линейная частота соответственно равны:

и 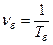. (3.16)

По рис.8 определим фазу биений :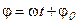

. (3.17)

Следовательно, вектор амплитуды суммарного колебания вращается с постоянной скоростью, равной полусумме циклических частот слагаемых колебаний.

Уравнение, характеризующее результирующее движение получим, если возьмем проекцию вектора на ось Х, учитывая :

. (3.18)

Графически биения представлены на Рис.9.

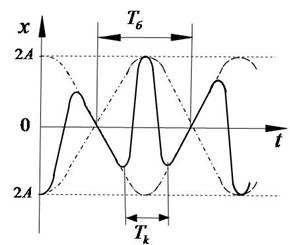
Амплитуда такого колебания то увеличивается, то уменьшается. Вспомним, что энергия колебаний пропорциональна квадрату амплитуды, следовательно, энергия биений тоже то увеличивается, то уменьшается, как и амплитуда.

СЛОЖЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ

ОДИНАКОВОЙ ЧАСТОТЫ

Рассмотрим результат сложения двух колебаний, происходящих во взаимно перпендикулярных направлениях.

Предположим, что материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях с одинаковыми периодами. Пусть колебания происходят по оси ОХ и ОУ. Запишем исходные уравнения:

. (3.19)

.

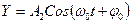Отметим, что разность фаз складываемых колебаний равна начальной фазе колебания вдоль оси У, т.к. частоты складываемых колебаний одинаковы, а начальную фазу колебаний вдоль оси Х мы приняли равной нулю -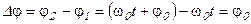

Чтобы определить траекторию движения точки, надо исключить из уравнений (3.19) время. Проделав ряд математических преобразований получим следующее уравнение:

;

. (3.20)

Возведем это уравнение в квадрат, чтобы избавиться от квадратного корня,

окончательно имеем:

(3.21)

Мы получили уравнение для траектории точки, участвующей одновременно в двух колебаниях во взаимно перпендикулярных направлениях. Это уравнение эллипса, характеристики которого определяются разностью фаз складываемых колебаний .

Разберем частные случаи:

1. Пусть . Уравнение траектории (3.21) принимает вид:

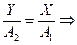, (3.22)

Это уравнение прямой, проходящей через начало координат и образующей с осью ОХ угол 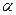, для которого 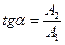. Вдоль этой прямой совершается гармоническое колебание, амплитуда которого равна (Рис.10).

2. Пусть . Уравнение траектории (3.21) принимает вид:

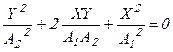
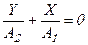
(3.23)

Опять получаем уравнение прямой линии, проходящей через начало координат и образующей с осью ОХ угол 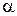, для которого . Вдоль этой прямой совершается гармоническое колебание, амплитуда которого равна (Рис.11).

Таким образом, в рассмотренных случаях, когда разность фаз при сложения двух взаимно перпендикулярных колебаний равна либо 0 либо π, получаем колебание с постоянной амплитудой 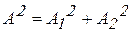вдоль прямой линии, направление которой определяет угол (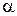) наклона прямой к оси ОХ, для которого .

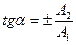3. Пусть 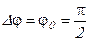. Уравнение траектории (3.21) принимает вид:

(3.24)

Траектория движения имеет форму эллипса, оси которого совпадают с осями ОХ и ОУ (рис.12).

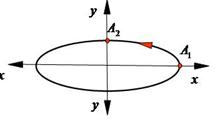
Точка описывает этот эллипс за время равное периоду складываемых колебаний. Если амплитуды складываемых колебаний равны, то форма траектории - окружность.

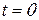Рассмотрим движение точки по эллиптической траектории при разности фаз . В момент времени материальная точка имеет координаты . В момент времени координаты точки - 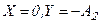. Таким образом, при заданной разности фазы складываемых колебаний движение материальной точки по эллипсу будет происходить по часовой стрелке.

При разности фаз движение материальной точки по траектории в форме эллипса будет происходить против часовой стрелки.

Таким образом, движение материальной точки по эллипсу (или окружности), можно представить, как колебание с изменяющейся по величине амплитудой в случае, когда траектория эллипс, и изменяющимся направлением колебания. За время равное периоду колебания конец вектора амплитуды описывает эллипс (или окружность). В зависимости от разности фаз складываемых колебаний движение точки происходит либо по часовой стрелке, либо против часовой стрелки.

Приведенные траектории движения материальной точки называют фигурами Лиссажу. Если взаимно перпендикулярные колебания происходят с разными частотами (периодами), то в результате сложения колебаний получаются траектории более сложной формы. Форма траектории определяется отношением частот складываемых колебаний.

Фигуры Лиссажу можно применять для определения частоты какого-либо гармонического колебания. Для этого на входы осциллографа надо подать два взаимно перпендикулярных колебания с известной и неизвестной частотами. Плавно изменяя известную частоту (она поступает от генератора электромагнитных колебаний), добиться устойчивой фигуры Лиссажу. По её виду - отношение частот складываемых колебаний равно отношению числа пересечений фигуры Лиссажу прямыми, параллельными осям координат – можно определить неизвестную частоту (Рис. 13).

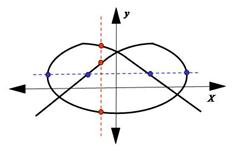
Для приведенного примера .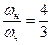

Дата добавления: 2014-01-07