
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Замена переменных
|
|
|
|
Представление фазных величин f А, f В, f С через обобщенный вектор f возможно при условии:
f А + f В + f С = 0.
Если сумма фазных переменных не равна нулю, то её целесообразно выразить через новое переменное f 0: f А + f В + f С = 3 f 0. Нулевая составляющая во всех фазах одинакова и тождественна составляющей нулевой последовательности. Фазные переменные, выраженные через обобщенный вектор:
f А = f cos α; f В = f cos(α - 2π/3); f c = f cos(α + 2π/3),
где α - угол между векторами f А и f (Рис.1)

Рис.1. Обобщенный вектор трехфазной системы
Обобщенный вектор можно определить как
f 2А + f 2В + f 2С = (3/2) f 2,
Откуда
f 
Обобщенный вектор можно выразить и в двухосной системе координат. В качестве последней удобно выбрать декартовые ортогональные координаты х и у или d и q (cовмещенные с магнитными осями ротора генератора, рис.2.).
Преобразование координат соответствует замене переменных. Проекции вектора f на оси х и у:
f Х = f cos(θ - α); f У = f sin(θ - α),
где θ - угол между магнитной осью фазы А и осью Х.
|
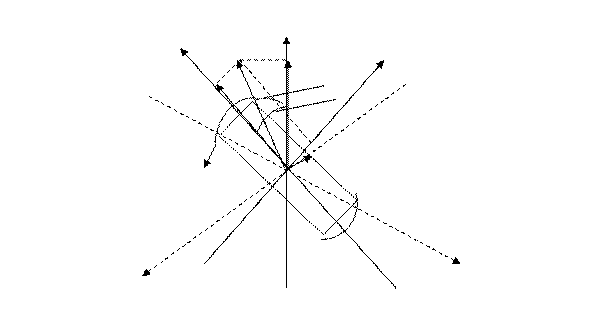
Рис.2. Преобразование координат
Применение новой системы координат сокращает переменные коэффициенты. Упрощения можно достичь, используя декартову систему координат, жестко связанную с ротором синхронной машины d, q и 0. Поскольку фазные обмотки, расположенные в осях d, q, неподвижны относительно ротора, индуктивности такой машины постоянны. Фазные переменные в системе координат d, q и 0:
f А =  cosγ +
cosγ + 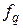 sinγ + f 0;
sinγ + f 0;
f В =  cos(γ - 2π/3) +
cos(γ - 2π/3) + 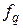 sin(γ - 2π/3) + f 0;
sin(γ - 2π/3) + f 0;
f С =  cos(γ + 2π/3) +
cos(γ + 2π/3) + 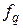 sin(γ + 2π/3) + f 0,
sin(γ + 2π/3) + f 0,
где γ = ωс t + γ0 – угол, характеризующий положение ротора в пространстве; ωс - синхронная угловая скорость, γ0 - начальный угол.
|
|
|
Фазные переменные напряжения, тока в системе координат d, q и 0:
U А = 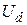 cosγ +
cosγ + 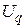 sinγ + U 0;
sinγ + U 0;
i А = 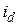 cos(γ - 2π/3) +
cos(γ - 2π/3) + 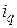 sin(γ - 2π/3) + i 0;
sin(γ - 2π/3) + i 0;
ΨА = Ψ d cos(γ + 2π/3) + Ψ q sin(γ + 2π/3) + Ψ0.
Подставляя фазные переменные в дифференциальное уравнение равновесия обмотки фазы А получим уравнения Парка-Горева
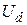 = -
= - 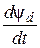 – Ψ q
– Ψ q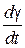 – R
– R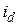 ; (1)
; (1)
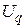 = -
= - 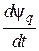 + Ψ d
+ Ψ d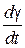 – R
– R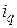 ;
;
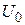 = -
= -  – R
– R ,
,
где 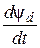 ,
, 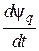 ,
,  – ЭДС трансформации, вызывается изменением величин потокосцеплений; Ψ q
– ЭДС трансформации, вызывается изменением величин потокосцеплений; Ψ q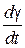 , Ψ d
, Ψ d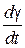 – ЭДС вращения (скольжения).
– ЭДС вращения (скольжения).
Потокосцепления в системе относительных единиц равны
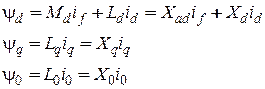
где 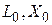 - индуктивность и индуктивное сопротивление нулевой последовательности машины.
- индуктивность и индуктивное сопротивление нулевой последовательности машины.
Таким образом переход к новым переменным в координатах d, q, 0 позволил преобразовать систему дифференциальных уравнений равновесия ЭДС и падений напряжений, где все коэффициенты постоянны.
Уравнения (1) выражают основу теории двух реакций синхронной машины при электромагнитном переходной процессе.
Для самостоятельного изучения - тема: Схемы замещения синхронной машины в продольной и поперечной осях ротора для начального момента переходного процесса
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1140; Нарушение авторских прав?; Мы поможем в написании вашей работы!