Понижение порядка дифференциального уравнения

Class CTest

Class CTest

{ public: int N;

static int GetN() {return N;}

}

Статический метод обладает следующими свойствами:

1. Вызов методы может быть произведен без ссылки на экземпляр класса.

Пример:

void main()

{

int Count=CTest::GetCount();

}

2. Статический метод класса может непосредственно ссылаться только на статические элементы данных и методы, которые принадлежат к его классу. (Статический метод не имеет указателя this, содержащего адрес объекта)

Статические данные и методы могут быть использованы для обработки элементов данных, общих для всех экземпляров класса.

Пример: подсчет текущего количества экземпляров класса.

#include<iostream.h>

{ private: Static int Count;

public:

CTest() { ++Count; }

~CTest() { --Count; }

static int GetCount() { return Count; }

}

Int CTest::Count=0;

void main()

{

cout<<” кол-во объектов: ”;

cout<<CTest::GetCount();

CTest Test1;

CTest *PTest2=new CTest;

cout<<” количество объектов: ”;

cout<<CTest::GetCount();

delete PTest2;

cout<<” количество объектов: ”;

cout<<CTest::GetCount();

}

Программа напечатает:

количество объектов: 0

количество объектов: 2

количество объектов: 1

До сих пор мы решали только дифференциальные уравнения первого порядка. Существуют дифференциальные уравнения высших порядков, которые сводятся к решению дифференциальных уравнений первого порядка. Простейший пример: . Очевидно, что для получения решения 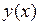достаточно дважды проинтегрировать правую часть. Заметим, что при первом интегрировании мы получаем постоянную интегрирования 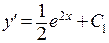. При втором интегрирование мы снова получаем постоянную интегрирования – уже другую: . Таким образом, решение дифференциального второго порядка содержит уже две произвольные постоянные. Очевидно, что решая подобное простейшее уравнение 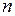-го порядка, мы получим 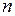произвольных постоянных. Следовательно, что для получения частного решения дифференциального уравнения 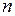-го порядка следует задавать 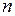дополнительных условий.

1.Уравнение вида 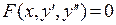. В этом случае следует взять за неизвестную функцию . Найдя , мы определим интегрированием.

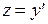П р и м е р. Решить уравнение . Введем функцию и решим уравнение с разделяющимися переменными 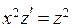. Получив его решение 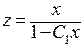, найдем исходную функцию : .

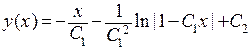Для выделения из множества решений единственного решения можно задать условия:. Например, .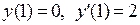

Из последнего условия мы получим 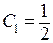, то есть .

Из первого условия получим . Теперь частное решение, удовлетворяющее двум дополнительным условиям, имеет вид

.

2. Уравнение вида . В этом случае целесообразно сделать замену . Заметим, что переменной во введенной функции является не 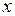– как в предыдущем случае, а . Теперь . Уравнение становится дифференциальным уравнением первого порядка. Решив его, то есть, найдя , мы получим 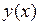как решение уравнения с разделяющимися переменными .

П р и м е р. Решить уравнение . Сделаем замену и запишем уравнение в виде 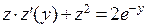. Очевидно, что здесь целесообразна еще одна замена: 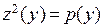. Уравнение принимает вид линейного уравнения первого порядка: 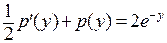. Решаем сначала соответствующее однородное (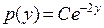), а затем ищем решение неоднородного уравнения в виде 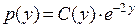. Подставляя в уравнение, получим , и значит, 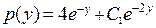. Следовательно, для определения функции 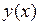мы имеем уравнения . Это уравнения с разделяющимися уравнениями, и мы должны восстановить первообразные по дифференциалам: . В результате получим решение: .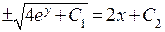

Для того, чтобы конкретизировать данное решение, то есть, определить значения , недостаточно одного начального условия при решении задачи Коши. В случае дифференциального уравнения второго порядка задача Коши имеет два начальных условия: 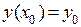и .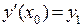

Для данного примера зададим следующие начальные условия: 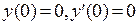. Тогда получим 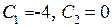. И решение примет вид 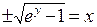или .

Дата добавления: 2014-01-14