Решение задач линейного программирования

Пример 1.

Построить математическую модель задачи линейного программирования.

Для изготовления продукции используется три вида сырья. При этом можно применять любой из четырех способов производства. Запасы сырья, расход и количество производимой продукции за один час работы по каждому способу приведены в таблице. Требуется найти план производства, при котором будет выпущено наибольшее количество продукции.

Способ произв-ва   Сырье					Запасы сырья
Выпуск продукции

Пусть x_j – время использования j-го способа производства, j=1,4.

f(x) = 24x₁ +14x₂+ 36x₃ +20x₄ àmax

Запишем полученную математическую модель задачи в канонической форме:

f¹ (x) = -24x₁ -14x₂ - 36x₃ - 20x₄ àmin

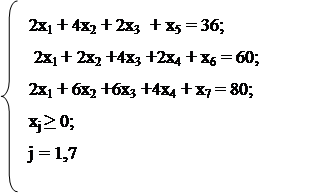Пример 2.

Решить задачу линейного программирования графическим методом.

f (x) = x₁ +3x₂ àmax

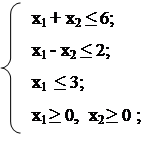Заменим в ограничениях знаки неравенств на знаки равенств и на основе полученных уравнений построим прямые.

1. x₁ + x₂ = 6 x₂

т. А₁ (0,6); т.А₂ (6,0).

2. x₁ - x₂ = 2

т. В₁ (0,-2); т.В₂ (2,0).

3. x₁ = 3

4. x₁ = 0, x₂ = 0. x₁

На графике показано, что каждое неравенство определяет некоторую полуплоскость. Соответствующие области для каждого ограничения отмечены штрихами. Пересечение D данных полуплоскостей (т.е. множество точек, которые одновременно принадлежат каждой из них) является областью допустимых планов задачи. Построим вектор С и прямую f (x) = x₁ +3x₂, проходящую через начало координат и перпендикулярную вектору С. Передвигая прямую f (x) в направлении вектора С, найдем точку в которой функция принимает максимальное значение.

Максимальное значение функция принимает в угловой точке x^* (0,6). Вычислим значение функции в этой точке: f (x^*) = 0 +3*6 = 18.

Пример 3.

Решить задачу симплекс методом на основе данных примера1.

Получить вариант оптимального плана производства для получения максимальной прибыли.

f(x) = 24x₁ +14x₂+ 36x₃ +20x₄ àmax

Канонический вид:

f¹ (x) = -24x₁ -14x₂ - 36x₃ - 20x₄ àmin

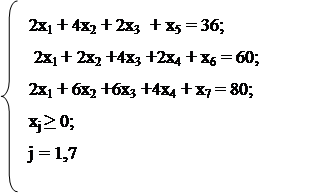Определим базисные и свободные переменные.

x₅, x₆, x₇ – базисные переменные;

x₁, x₂, x₃, x₄ – свободные переменные.

Составим симплекс-таблицу.

Чтобы определить разрешающий столбец необходимо выбрать наименьший элемент в последней строке симплекс-таблице. Далее необходимо определить разрешающий элемент, составив симплекс-отношения:

36/4=9, 60/2=30, 80/6=13,3.

Наименьшим является первое симплекс-отношение, следовательно разрешающий элемент находится на пересечении 3-й строки и 4-го столбца.

Симплекс - Метод
БП	СЧ	Х1	Х2	Х3	Х4	x5	x6	x7
Х5
Х6
x7
F(X)

Переходим к следующей симплекс-таблице.

Делим разрешающую строку на 4 и выполняем преобразования симплекс-таблицы так, чтобы в разрешающем столбце получить нули (кроме разрешающего элемента). Подобные действия выполняются до тех пор пока в последней строке все6 элементы не станут отрицательными. Неизвестные переменные, соответствующие разрешающей строке и столбцу меняют местами при переходе к новой симплекс-таблице.

БП	СЧ	Х1	Х2	Х3	Х4	x5	x6	x7
Х5		0,5		0,5		0,25
Х6						-0,5
x7		-1				-1,5
F(X)	-126					-3,5

БП	СЧ	Х1	Х5	Х3	Х4	x5	x6	x7
Х2						0,5
Х6			-2			-1
x7						-1
F(X)	-432		-34			-12
БП	СЧ	Х2	Х2	Х3	Х4	x5	x6	x7
Х1			1,5		-1	0,75		-0,25
Х6			-3			-0,5		-0,5
x7			0,5			-0,25		0,25
F(X)	-564		-40			-9		-3
БП	СЧ	Х1	Х2	Х7	Х4	x5	x6	x7
Х5						0,5
Х6			-3			-0,5		-0,5
x3			0,5			-0,25		0,25
F(X)	-88		-4	-8	-8			-2
БП	СЧ	Х1	Х2	Х3	Х3	x5	x6	x7
Х5
Х6			-1					-0,5
x4		0,5	1,5	1,5				0,25
F(X)	-160	-4	-12	-12	-8			-2

В последней строке нет положительных, следовательно, оптимальное решение найдено:

Fmin(x) = -160, x^* (0,0,0,20,36,20,0).

Fmax = - Fmin= 160.

Пример 4.

Построить математическую модель задачи и решить ЗЛП графическим способом.

Предприятие располагает 3 видами сырья и может выпускать одну и туже продукцию 2-мя способами. При этом за один час работы первым способом выпускается 30 единиц продукции, а вторым 45 единиц продукции. Количество сырья (кг) трех видов, расходуемое за один час работы при различных способах производства и запасы сырья приведены в таблице. Требуется найти план производства, при котором будет выпущено наибольшее количество продукции.

Способ производства	Сырье
			22,5
			22,5
Запасы сырья

Пусть x₁, x₂ – время использования первого и второго способа.

Тогда математическая модель задачи будет иметь вид:

f(x) = 30x₁ +45x₂ àmax

x₂

1. 15x₁ + 30x₂ = 150

т. А₁ (0,5); т.А₂ (10,0).

2. 30x₁ + 15x₂ ≤ 150

т. В₁ (0,10); т.В₂ (5,0).

3. 22,5x₁ + 22,5x₂ = 135

т. С₁ (0,6); т.С₂ (6,0). x₁

4. x₁ = 0, x₂ = 0.

Максимальное значение функция принимает в ^* (2,4). Вычислим значение функции в этой точке: f (x^*) = 2*30+45*4 = 240.

Для производства наибольшего количества продукции при имеющихся запасах сырья необходимо два часа применять первый способ и четыре часа - второй способ. При этом будет изготовлено 240 единиц продукции.

Пример 5.

Решить задачу линейного программирования симплекс-методом.

f(x) = 2x₁ +x₂ - x₃ +x₄ – x₅àmax

Решение:

f ¹(x) =-2x₁ -x₂ + x₃ -x₄ + x₅àmin

x_3, x_4, x₅ – базисные переменные;

x_1, x₂ - свободные переменные.

x₃ = 5- x₁ - x₂

x₄ = 9 - 2x₁ - x₂

x₅ = 7+ x₁ -2x₂

Тогда f (x) =-2x₁ -x₂ +5 - x₁ - x₂ - 9 + 2x₁ + x₂ + 7+ x₁ -2x₂ = 3-3x₂

Составим симплекс-таблицу, определим разрешающий столбец, разрешающий элемент.

Наименьшим является первое симплекс-отношение, следовательно разрешающий элемент находится на пересечении 5-й строки и 4-го столбца.

Симплекс - Метод
БП	СЧ	Х1	Х2	Х3	Х4	x5
Х3
Х4
x5		-1
F(X)

Выполним необходимые преобразования для получения в последней строке отрицательных элементов.

Симплекс - Метод
БП	СЧ	Х1	Х2	Х3	Х4	x5
Х3	1,5	1,5				-0,5
Х4	5,5	2,5				-0,5
x5	3,5	-0,5				0,5
F(X)	-7,5	1,5				-1,5
Симплекс - Метод
БП	СЧ	Х3	Х5	Х3	Х4	x5
Х1				0,6		-0,3
Х4				-1,5		0,25
x2				0,3		0,35
F(X)	-9			-0,9		-1,05

В последней строке нет положительных элементов, следовательно, оптимальное решение найдено:

Fmin(x) = -9, x^* (1,4,0,3,0).

f ¹(x) =-2 -4 + 0 -3 + 0 = -9.

Пример 6.

Из трех продуктов - I, II, II составляется смесь. В состав смеси должно входить не менее 24 ед. химического вещества А, 32 ед.- вещества В и не менее 48 ед. вещества С. Структура химических веществ приведена в следующей таблице:

Продукт	Содержание химического вещества в 1 ед. продукции	Стоимость 1 ед. продукции
А	В	С
I
II
III

Необходимо составить наиболее дешевую смесь.

Решение:

Пусть x_j – количество продукта, j=1,3.

Математическая модель:

f(x) = 8x₁ +12x₂ + 10x₃ àmin

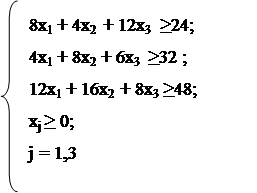Канонический вид:

f¹(x) = -8x₁ - 12x₂ - 10x₃ àmax

Составим симплекс-таблицу.

Симплекс - Метод
БП	СЧ	Х1	Х2	Х3	Х4	x5	x6
Х4					-1
Х5						-1
x6							-1
F(X)
Симплекс - Метод
БП	СЧ	Х1	Х2	Х3	Х4	x5	x6
Х4			0,5	1,5	-0,125
Х5					0,5	-1
x6				-10	1,5		-1
F(X)	-24			-2
Симплекс - Метод
БП	СЧ	Х4	Х2	Х3	Х4	x5	x6
Х1			1,33	0,67			-0,08
Х5			2,67	3,33		-1	0,33
x6			6,67	-6,67			-0,67
F(X)	-32		1,33	4,67			0,67
Симплекс - Метод
БП	СЧ	Х4	Х2	Х3	Х6	x5	x6
Х1	7,88		1,98	1,48		-0,24
Х5			2,67	3,33		-1	0,33
x4	40,48		12,09	0,09		-2,03
F(X)	-64,48		-4,09	-2,09		2,03
Симплекс - Метод
БП	СЧ	Х4	Х2	Х3	Х6	x5	x5
Х1	7,88		1,98	1,48		-0,24
Х6			2,67	3,33		-1	0,33
x4	40,48		12,09	0,09		-2,03
F(X)	-64,48		-4,09	-2,09		2,03

Выбор разрешающего элемента невозможен, так как все элементы разрешающего столбца отрицательны по знаку. Следовательно задача не имеет решений.

Пример 7.

Решить задачу графическим методом.

f(x) = 2x₁ +5x₂ àэкстремум

x₂

1. 2x₁ + 5x₂ = 25

т. А₁ (0,5); т.А₂ (12,5;0).

2. x₁ - x₂ = 2

т. В₁ (0,-2); т.В₂ (2,0).

3. x₁ = 0, x₂ = 0.

x₁

Ответ: x_min^* (0,0); x_max^** (5,3); f (x_min^*) = 25; f(x_max^**) = 0.

Пример 8.

Требуется перевезти груз из трех пунктов отправления в пять пунктов назначения.

Z(x) = 2x₁₁ + 4x₁₂ + 5x₁₃ +7x₁₄ + 9x₁₅ +x₂₁ + x₂₂ + 3x₂₃ +5x₂₄ + 4x₂₅ + 6x₃₁ + 3x₃₂ + 2x₃₃ +x₃₄ + 10x₃₅àmin

x₁₁ + x₁₂ + x₁₃ +x₁₄ + x₁₅ = 300; x₂₁ + x₂₂ + x₂₃ +x₂₄ + x₂₅ = 400; x₃₁ + x₃₂ + x₃₃ +x₃₄ + x₃₅ = 900;   x₁₁ + x₂₁ + x₃₁ = 250; x₁₂ + x₂₂ + x₃₂ = 300; x₁₃ + x₂₃ + x₃₃ = 350; x₁₄ + x₂₄ + x₃₄ = 500; x₁₅ + x₂₅ + x₃₅ = 200; x_j ≥ 0; i=1,2,3; j=1,…,5.  

Решение:

Исходные данные задачи удобно представить в виде таблицы.

	В1	В2	В3	В4	В5	Наличие
А1
А2
А3
Потребность

Опорный план, представленный в таблице, получен с использованием метода северо-западного угла.

Необходимо рассчитать стоимость перевозок для данного плана:

Z = 2*250 + 4*50 + 1*250 + 3*150 + 2*200 + 1*500 + 10*200 = 4300

Используя систему потенциалов, каждому поставщику присвоим потенциал u_i, а каждому столбцу-потребителю присвоим потенциал v_j.

Расчет потенциалов производится по формуле 11.

	В1	В2	В3	В4	В5	Наличие	Ui
А1
А2			3 _		4 +
А3			2 +		10 _
Потребность
Vj

Например: U₁ = 0; 2 = V₁ - U₁

2 = V₁ – 0

V₁ = 2.

Проверим решение на оптимальность путем составления матрицы оценок (формула 12).

0 0 -1 2 -5 2 0 0 3 -7 8 3 0 0 0

d =

В матрице есть отрицательные элементы, следовательно решение не оптимально. Согласно правилу переноса выбирается прямоугольник, расставляются знаки и проверяется условие ∑ с⁺ < ∑ с^-. 6 < 13, следовательно план перевозок улучшится. Свободная вершина отмечается знаком «-», вторая вершина (движение по часовой стрелке) знаком минус, третья – знаком плюс и четвертая – знаком минус. В клетки, отмеченные знаком «+» добавляется минимальное количество груза, из клеток со знаком «-» вычитается это же количество груза.

	В1	В2	В3	В4	В5	Наличие	Ui
А1
А2
А3							-3
Потребность
Vj			-1	-2

Z = 250*2+50*4+250*1+150*4+350*2+500*1+50*10 = 3250

3250 < 4300, значит решение улучшено. Но решение не является оптимальным, т.к. матрица d содержит отрицательные элементы.

d=

В матрице d выбирается прямоугольник, так чтобы угловая вершина имела знак «-», а три другие были заполненные.

	В1	В2	В3	В4	В5	Наличие	Ui
А1
А2		1 _			4 +
А3		3 +			10 _		-3
Потребность
			-1	-2

В клетки, отмеченные знаком «+» добавляется минимальное количество груза (50), из клеток со знаком «-» вычитается это же количество груза.

	В1	В2	В3	В4	В5	Наличие	Ui
А1
А2
А3
Потребность
Vj

Стоимость данного плана перевозок: Z = 250*1+50*4+200*1+200*4+50*3 = 3050.

0 0 2 5 2 2 0 3 6 0 5 0 0 0 4  

d =

В матрице нет отрицательных элементов, следовательно решение оптимальное и наименьшая стоимость перевозок равна 3050.

Пример 9.

Решить транспортную задачу: перевезти груз из трех пунктов отправления в пять пунктов назначения.

Z(x) = 21x₁₁ + 18x₁₂ + 14x₁₃ +3x₁₄ + 6x₁₅ +7x₂₁ + 11x₂₂ + 10x₂₃ +5x₂₄ + 12x₂₅ + 4x₃₁ + 8x₃₂ + 12x₃₃ +8x₃₄ + 13x₃₅àmin

x₁₁ + x₁₂ + x₁₃ +x₁₄ + x₁₅ = 370; x₂₁ + x₂₂ + x₂₃ +x₂₄ + x₂₅ = 450; x₃₁ + x₃₂ + x₃₃ +x₃₄ + x₃₅ = 430;   x₁₁ + x₂₁ + x₃₁ = 300; x₁₂ + x₂₂ + x₃₂ = 230; x₁₃ + x₂₃ + x₃₃ = 330; x₁₄ + x₂₄ + x₃₄ = 290; x₁₅ + x₂₅ + x₃₅ = 100; x_j ≥ 0; i=1,2,3; j=1,…,5.  

Решение:

МЕТОД СЕВЕРО-ЗАПАДНОГО УГЛА

В1

В2

В3

В4

В5

Наличие

А1

А2

А3

Потр-ть

Z

МЕТОД НАИМЕНЬШЕГО ЭЛЕМЕНТА

В1

В2

В3

В4

В5

Наличие

А1

А2

+

-6

А3

-3

Потр-ть

Z

МАТРИЦА I

d

-4

УЛУЧШЕНИЕ ВТОРОГО ВАРИАНТА

В1

В2

В3

В4

В5

Наличие

А1

А2

-2

А3

Потр-ть

Z

МАТРИЦА II

d

Решение оптимально, т.к. матрица не содержит отрицательных элементов.

Наименьшая стоимость перевозок равна 8150.

Пример 10.

Имеются три сорта бумаги в количестве 10, 8 и 5 тонн, которую можно использовать на издание четырех книг тиражом 8000, 6000, 15000, 10000 экземпляров. Расход бумаги на одну книгу составляет: 0,6; 0,8; 0,4; 0,5 кг., а себестоимость тиража книги при использовании i-го сорта бумаги задается следующей матрицей (д.е.):

C_ij =

Определить оптимальное распределение бумажных ресурсов.

Решение:

Задача по своему экономическому смыслу не является транспортной, в то же время можно построить математическую модель, аналогичную транспортной задаче.

Потребности в бумаге легко определить, зная тираж и расход на одну книгу:

8000*0,6=4,8 т;

15000*0,4=6 т;

6000*0,8=4,8 т;

10000*0,5=5 т.

Общие запасы бумаги составляют 23 т, а общие потребности – 20,5 т, поэтому необходимо в таблицу ввести фиктивный тираж В₅ ^* с нулевыми затратами. В связи с тем что модель составляется относительно бумаги, а матрица C_ij характеризует себестоимость печатания книги, необходимо исходную матрицу преобразовать относительно единицы бумаги (каждый столбец матрицы C_ij необходимо разделить на количество бумаги, приходящейся на одну книгу).

Согласно изложенному составляется первая таблица.

Потребители   Поставщики	В1	В2	В3	В4	В5^*	Запасы, т
А1
А2
А3
Потребность,т	4,8	4,8			2,4

Используя метод потенциалов, получим оптимальное решение.

Потребители   Поставщики	В1	В2	В3	В4	В5^*	Запасы, т
А1		4,8		502,8
А2	4,8			2,2
А3
Потребность,т	4,8	4,8			2,4

Анализ решения.

Бумаги первого сорта в количестве 4,8 т затрачено на издание второй книги; 2,8 т – на издание четвертой книги; 2,4 т – не использовано.бумаги второго сорта затрачено: на первую книгу – 4,8 т; на издание третьей книги 1,0 т; на издание четвертой книги – 2,2 т; бумага третьего сорта использована на издание третьей книги в количестве 5 т.

Дата добавления: 2014-01-15