
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Для систем с конечным числом степеней свободы, например, при расчете методом перемещений
|
|
|
|

Энергетический метод основан на исследовании полной потенциальной энергии  , накапливаемой системой при ее переходе из заданного состояния равновесия в деформированное критическое равновесное состояние.
, накапливаемой системой при ее переходе из заданного состояния равновесия в деформированное критическое равновесное состояние.
Критерием, устойчивости является теорема Дирихле: при равновесии приращение полной потенциальной энергии системы  при любом возможном отклонении равно нулю, т.е. полная потенциальная энергия системы имеет экстремальное значение. При этом исследуется переход от начального равновесного состояния к близкому ему - изогнутому. Приращение полной потенциальной энергии системы находится по формуле
при любом возможном отклонении равно нулю, т.е. полная потенциальная энергия системы имеет экстремальное значение. При этом исследуется переход от начального равновесного состояния к близкому ему - изогнутому. Приращение полной потенциальной энергии системы находится по формуле
 .
.


При возможном отклонении стержня от равновесного положения первая вариация от полной энергии должна быть равна нулю:
 .
.
Об устойчивости равновесного положения можно судить по знаку второй вариации от полной энергии: если исходное положение устойчиво, то вторая вариация положительна (потенциальная энергия системы минимальна по сравнению с энергией для отклоненных положений):
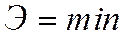 ,
,  .
.
Если вторая вариация отрицательна, то рассматриваемая равновесная форма будет неустойчивой (потенциальная энергия системы имеет максимум):
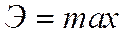 ,
, 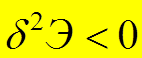 .
.
Безразличному равновесному состоянию соответствует равенство нулю второй вариации, т.е. потенциальная энергия при всех отклонениях от исследуемого положения постоянна:
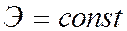 ,
, 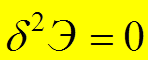 .
.
Величины критических нагрузок определяются из следующего условия: критическому состоянию соответствует состояние безразличного равновесия, т.е., составив выражение полной потенциальной энергии системы, при ее переходе из заданного состояния равновесия в деформированное состояние как функции параметров 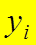 , число которых равно степени свободы системы.
, число которых равно степени свободы системы.
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 526; Нарушение авторских прав?; Мы поможем в написании вашей работы!