
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЛЕКЦИЯ 6. Случайный процесс как модель сигнала
|
|
|
|
Случайный процесс как модель сигнала.
Единственная то что определяемая во времени функция не может служить математической моделью сигнала при получении, передачи и преобразовании информации. Поскольку получение информации связано с устранением априорной неопределенности исходных состояний, однозначная функция времени только тогда будет нести информацию, когда она с определенной вероятностью выбрана из множества возможных функций. Поэтому в качестве моделей сигнала используется служебный процесс. Каждая выбранная детерминированная функция рассматривается как реализация этого случайного процесса.
Необходимо учитывать воздействие на полезный сигнал помех, которые по своей природе случайны. Математическая модель помехи представляется также в виде случайного процесса, параметры которого определяются экспериментально. Вероятностные свойства помехи, как правило, отличны от свойств полезного сигнала, что и лежит в основе методов их разделения.
Справка. Под случайным процессом (стохастическим) подразумевают такую случайную функцию времени U(t), значение которой в каждый момент времени случайны. Конкретный вид U(t) называют реализацией случайного процесса. Точно ее предсказать невозможно. Можно лишь определить статистические данные, характеризующие все множество конкретных реализаций, называемое ансамблем.
Основными признаками, по которым классифицируются случайные процессы, являются: пространство состояний, временной параметр и статистические зависимости между случайными величинами U(ti) в разные моменты времени ti.
Пространство состояний называют множество возможных значений случайной величины U(ti). Случайный процесс, у которого множество состояний составляет континуум, а изменение состояний возможны в любые моменты времени, называют непрерывным случайным процессом.
|
|
|
Если же изменения состояний допускаются лишь в конечном или счетном числе моментов времени, то говорят о непрерывной случайной последовательности.
Случайный процесс с конечным множеством состояний, которые могут изменяться в произвольные моменты времени, называют дискретным случайным процессом. Если же изменения состояний возможны только в конечном или счетном числе моментов времени, то говорят о дискретных случайных последовательностях.
Примеры реализации указанных случайных процессов представлены на рис. 3.
В настоящее время чаще имеют дело с дискретными случайными последовательностями.
Среди случайных процессов с дискретным множеством состояний нас будут интересовать такие, у которых статистические зависимости распространяются на ограниченное число k следующих друг за другом значений. Они называются обобщенными Марковскими процессами k-го порядка.
Вероятностные характеристики случайного процесса.
В соответствии с определением случайный процесс U(t) может быть описан системой N обычно зависимых случайных величин U1 = U(t1), …, Ui = U(ti), …, UN=U(tN), взятых в различные моменты времени t1, …, ti, …, tN. При N®¥ такая система эквивалентна рассматриваемому случайному процессу U(t).
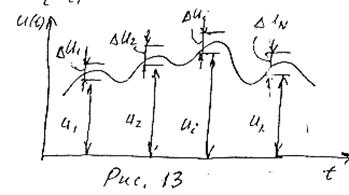
 Исчерпывающей характеристикой доказанной системы является N – мерная плотность вероятности PN(U1, …, Ui, …, UN, t1, …, ti, …, tN). Она позволяет вычислить вероятность PN реализации, значения которой в моменты времени t1, ti, tN будут находиться соответственно в интервалах (u1, u1 + Du1),…, (ui, ui + Dui), …,(uN, uN +DuN), где ui(i=1, N)– значение, принимаемое случайной величиной Ui (рис. 13).
Исчерпывающей характеристикой доказанной системы является N – мерная плотность вероятности PN(U1, …, Ui, …, UN, t1, …, ti, …, tN). Она позволяет вычислить вероятность PN реализации, значения которой в моменты времени t1, ti, tN будут находиться соответственно в интервалах (u1, u1 + Du1),…, (ui, ui + Dui), …,(uN, uN +DuN), где ui(i=1, N)– значение, принимаемое случайной величиной Ui (рис. 13).
Если Dui выбираем достаточно малыми, то справедливо соотношение
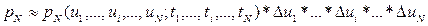
Экспериментальное получение величины 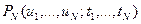 крайне сложно, а последующее использование результатов наталкивается на существенные математические трудности.
крайне сложно, а последующее использование результатов наталкивается на существенные математические трудности.
|
|
|
На практике обычно ограничиваются одно- или двумерной плотностью вероятности.
Одномерная плотность вероятности 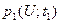 случайного процесса U(t) характеризует распределение одной случайной величины U1 взятой в произвольный момент времени t1. В ней не находит отражения зависимость случайных величин в различные моменты времени.
случайного процесса U(t) характеризует распределение одной случайной величины U1 взятой в произвольный момент времени t1. В ней не находит отражения зависимость случайных величин в различные моменты времени.
Двумерная плотность вероятности 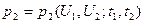 позволяет определить вероятность совместной реализации любых двух значений случайных величин
позволяет определить вероятность совместной реализации любых двух значений случайных величин 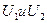 в произвольные моменты времени t 1 и t 2 и, следовательно, оценить динамику развития процесса. Одномерную плотность вероятности случайного процесса U (t) можно получить из двумерной плотности, воспользовавшись соотношением:
в произвольные моменты времени t 1 и t 2 и, следовательно, оценить динамику развития процесса. Одномерную плотность вероятности случайного процесса U (t) можно получить из двумерной плотности, воспользовавшись соотношением:
 (67)
(67)
Использование плотности вероятности даже низших порядков часто приводит к неоправданным трудностям. В большинстве случаев достаточно знать простейшие характеристики случайного процесса, аналогичные числовым характеристикам случайных величин. Наиболее распространены моменты функции первых двух порядков: математическое ожидание, дисперсия и корреляционная функция.
Математическим ожиданием случайного процесса U (t) называют неслучайную функцию времени m u(t 1), которая при любом аргументе ti равна среднему значению случайной величины U (t 1) по всему множеству возможных реализаций:
 (68)
(68)
Степень разброса случайных значений процесса U (t 1) от своего среднего значения m u(t 1) для каждого t 1 характеризуется дисперсией D U(t 1):
|
 (69)
(69)
где U (t 1)= U (t 1) - m u(t 1) – центрированная случайная величина
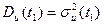 (70)
(70)
где  - среднеквадратическое отклонение.
- среднеквадратическое отклонение.
Случайные процессы могут иметь одинаковые математические ожидания и дисперсии (рис. 14, а, б), однако резко различаться по быстроте изменения своих значений во времени.
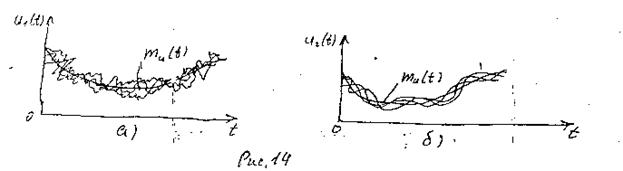
Для оценки статистической зависимости мгновенных значений процесса u (t) в произвольные моменты времени t 1 и t 2 R u(t 1, t 2), называемая автокорреляционной или просто корреляционной функцией.
При конкретных аргументах t 1 и t 2 она равна корреляционному моменту значений процесса U (t 1)и U (t 2):
 (71)
(71)
Через двумерную плотность вероятности выражение (71) представляется в виде
|
|
|
 (72)
(72)
В силу симметричности этой формулы относительно аргументов справедливо равенство
 (73)
(73)
Для сравнения различных случайных процессов вместо корреляционной функции удобно пользоваться нормированной функцией автокорреляции:
 (74)
(74)
При произвольном t 1 = t 2 автокорреляционная функция вырождается в дисперсию
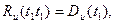 (75)
(75)
а нормированная функция автокорреляции равна единице
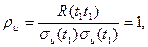 (76)
(76)
т.е. дисперсия случайного процесса является частным значением автокорреляционной функции.
Аналогично устанавливается мера связи между двумя случайными процессами u (t) и U (t). Она оказывается функцией взаимной корреляции
 (77)
(77)
Стационарные и эргодические случайные процессы.
 |
Справка. Случайные процессы различаются по степени однородности протекания их во времени. В общем случае процесс может иметь определенную тенденцию развития и характеристики, зависящие от начала отсчета времени. Такие случайные процессы называются нестационарными. Для описания сигнала математическая модель в виде нестационарного случайного процесса подходит наилучшим образом, но неконструктивна в силу своей чрезмерной сложности.
Поэтому очень часто вводят предположение о стационарности случайного процесса, что позволяет существенно упростить математический аппарат исследований.
Случайный процесс называют стационарным в узком смысле, если выражения для плотностей вероятности не зависят от начала отсчета времени, т.е. справедливо соотношение
 (78)
(78)
где  - случайная величина, отражающая значение процесса в момент времени t = t i + t (t - произвольное число).
- случайная величина, отражающая значение процесса в момент времени t = t i + t (t - произвольное число).
Иначе говоря, стационарность процесса предполагает его существование и статистическую однородность во всем диапазоне времени от -¥ до +¥.
_______________________________________________________________________
Справка. Такое предположение противоречит физически и свойства реальных сигналов, в частности тому, что всякий реальный сигнал существует только в течение конечного отрезка времени. Однако аналогично установившимся детерминированным процессам случайные процессы, протекающие в установившемся режиме работы системы при неприятных внешних условиях на определенных отрезках времени, с известным приближением можно рассматривать как стационарные.
|
|
|
_______________________________________________________________________
При решении многих задач идут на дальнейшее упрощение модели, рассматривая случайный процесс стационарным в широком смысле.
Процесс U(t) принято называть стационарным в широком смысле, если выполняется условие постоянства математического ожидания и дисперсии, а, корреляционная функция не зависит от начала отсчета времени и является функцией только одного аргумента t = t2 - t 1,т.е.
 (79)
(79)
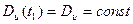 (80)
(80)
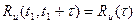 (81)
(81)
Т.к. условие постоянства дисперсии является частным случаем требования к корреляционной функции при t = 0:
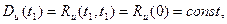
то выполнение соотношений (79) и (81) достаточно, чтобы рассматривать случайный процесс U(t) как стационарный.
Всякий стационарный случайный процесс является стационарным в широком смысле.
Случайные процессы, наблюдаемые в устойчиво работающих реальных системах, имеют конечное время корреляции. Поэтому для стационарных процессов, представляющих практический интерес, справедливо соотношение
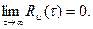 (82)
(82)
Если для случайного процесса равенства (79), (81) не выдерживаются, но на интересующем нас интервале времени изменением указанных параметров можно пренебречь, его называют квазистационарным.
Среди стационарных случайных процессов многие удовлетворяют свойству эргодичности. Оно проявляется в том, что каждая реализация случайного процесса достаточной продолжительности несет практически полную информацию о свойствах всего ансамбля реализаций, что позволяет существенно упростить процедуру определения статистических характеристик, заменяя усреднение значений по ансамблю реализаций усреднением значений одной реализации за длительный интервал времени.
Следовательно, для стационарных эргодических процессов справедливы соотношения
 (83)
(83)
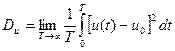 (84)
(84)
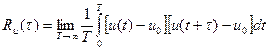 (85)
(85)
где u(t) – конкретная реализация случайного процесса U(t).
Результаты исследования случайных процессов в их временном представлении, т.е. с использованием формул (83), (84), (85), лежат в основе корреляционной теории сигналов.
_______________________________________________________________________
Для облегчения практического определения корреляционной функции в соответствии с (85) серийно выпускаются специальные вычислительные устройства – коррелометры (корреляторы).
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 1703; Нарушение авторских прав?; Мы поможем в написании вашей работы!