
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Відповідь
|
|
|
|
Якщо квадратна нерівність (1) виконується при великих значеннях, то вона виконується поза відрізком, обмеженим коренями рівняння. Якщо нерівність (1) не виконується при великих значеннях, то вона виконується на відрізку, обмеженому коренями рівняння (1).
Приклад. Розв’язати нерівність 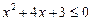 .
.
Ø Оскільки нерівність не виконується при великих значеннях 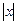 , то вона виконується між коренями рівняння
, то вона виконується між коренями рівняння  ,
,  , тобто при
, тобто при  .
.
Приклад. Розв’язати нерівність  .
.
Ø Дана нерівність виконується при великих значеннях 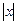 , тому вона виконується поза інтервалом, обмеженим коренями рівняння
, тому вона виконується поза інтервалом, обмеженим коренями рівняння 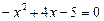 , тобто при
, тобто при 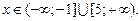
Часто доводиться розв’язувати нерівність виду
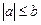 , (2)
, (2)
рівносильну системі нерівностей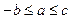 .
.
Приклад. Розв’язати нерівність
 .
.
Ø За формулою (2) дістаємо систему нерівностей:
 , звідки
, звідки 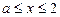 .
.
9.4. Метод інтервалів
Метод інтервалів застосовується при розв’язуванні будь-яких нерівностей, але найчастіше до нього вдаються, розв’язуючи раціональні нерівності виду
 , (1)
, (1)
де  — натуральні показники степеня. Щоб розв’язати таку нерівність, знаходимо корені многочлена в лівій її частині і позначають їх на числовій осі. Далі проводимо криву (орієнтовний графік цього многочлена) так, щоб вона проходила над віссю, коли многочлен (1) додатний і під віссю, коли цей многочлен від’ємний. Якщо многочлен не має квадратних коренів
— натуральні показники степеня. Щоб розв’язати таку нерівність, знаходимо корені многочлена в лівій її частині і позначають їх на числовій осі. Далі проводимо криву (орієнтовний графік цього многочлена) так, щоб вона проходила над віссю, коли многочлен (1) додатний і під віссю, коли цей многочлен від’ємний. Якщо многочлен не має квадратних коренів  то зазначена крива ніде не дотикається до осі, а лише перетинає її в точках, які відповідають кореням многочлена. Тому достатньо визначити знак многочлена в якомусь одному інтервалі, на які поділяють числову вісь корені многочлена, щоб дізнатися, в яких інтервалах графік розглядуваного многочлена міститься вище від осі, а в яких — нижче, тобто при яких значеннях x даний многочлен додатний, а при яких від’ємний. При переході через кратний корінь
то зазначена крива ніде не дотикається до осі, а лише перетинає її в точках, які відповідають кореням многочлена. Тому достатньо визначити знак многочлена в якомусь одному інтервалі, на які поділяють числову вісь корені многочлена, щоб дізнатися, в яких інтервалах графік розглядуваного многочлена міститься вище від осі, а в яких — нижче, тобто при яких значеннях x даний многочлен додатний, а при яких від’ємний. При переході через кратний корінь 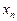 крива залишається з того самого боку від осі х бік, якщо показник
крива залишається з того самого боку від осі х бік, якщо показник 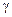 парний, і переходить на інший відносно осі х бік, якщо показник
парний, і переходить на інший відносно осі х бік, якщо показник 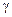 непарний.
непарний.
|
|
|
Приклад. Розв’язати нерівність
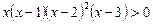 .
.
Ø Позначаємо корені  на осі х і зображуємо криву, що визначає знаки лівої частини нерівності (рис. 1).
на осі х і зображуємо криву, що визначає знаки лівої частини нерівності (рис. 1).
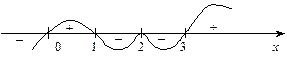
Рис. 1.
Нерівність має розв’язок 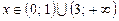 .
.
Приклад. Розв’язати нерівність
 .
.
Ø Розкладемо ліву частину нерівності на множники:
 .
.
Поділивши обидві частини нерівності на множники  і
і  які завжди додатні, дістанемо:
які завжди додатні, дістанемо:
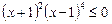 .
.
Відкладаємо на числовій осі точки 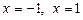 (рис. 2).
(рис. 2).

Рис. 2.
Отже, даний многочлен скрізь додатний, крім двох точок  , які є розв’язками нерівності.
, які є розв’язками нерівності.
Приклад. Розв’язати раціональну нерівність
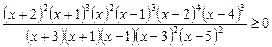 .
.
Ø Відкладаємо на числовій осі точки 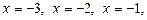
 , в яких ліва частина нерівності може змінити свій знак (рис. 3).
, в яких ліва частина нерівності може змінити свій знак (рис. 3).

Рис. 3.
Точки  , в яких нерівність не виконується, позначаємо порожнім кружечком. Отже, маємо такий розв’язок нерівності:
, в яких нерівність не виконується, позначаємо порожнім кружечком. Отже, маємо такий розв’язок нерівності:

9.5. Ірраціональні нерівності
Ірраціональні нерівності зводяться, як правило, до однієї з двох таких нерівностей:
 ; (1)
; (1)
 . (2)
. (2)
Нерівність (1) виконується в одному з двох випадків:

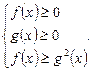
Нерівність (2) виконується, якщо виконуються нерівності:
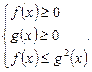
Приклад. Розв’язати нерівність
 .
.
Ø Маємо нерівність виду (1). Розв’яжемо системи нерів-
ностей:


Остаточно знаходимо розв’язок 
Приклад. Розв’язати ірраціональну нерівність
 .
.
Ø Маємо нерівність виду (2), розв’язання якої таке:
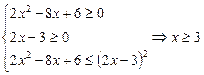 .
.
Приклад. Розв’язати нерівність
 .
.
Розв’язуємо окрему нерівність і рівняння:
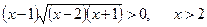 ;
;
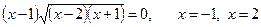 .
.
Остаточно дістаємо розв’язок 
Приклад. Розв’язати нерівність
 .
.
Ø Розв’язуючи окремо нерівність і рівняння, дістаємо:
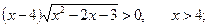
 .
.
Остаточно маємо розв’язок 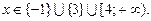
Кожну ірраціональну нерівність можна розв’язати методом інтервалів. Для цього знаходять її ОДЗ, а далі замінюють нерівність рівністю і розв’язують рівняння. Точки, що відповідають розв’язкам, розбивають ОДЗ на інтервали. Якщо в одній точці деякого інтервалу нерівність виконується, то вона виконується в усіх точках цього інтервалу. І навпаки: якщо в будь-якій одній точці інтервалу нерівність не виконується, то вона не виконується в усіх його точках.
|
|
|
Приклад. Розв’язати методом інтервалів нерівність
 . (3)
. (3)
Ø З нерівності  знаходимо ОДЗ:
знаходимо ОДЗ:
 Далі замість нерівності (3) розв’язуємо рівняння
Далі замість нерівності (3) розв’язуємо рівняння 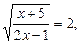 або
або 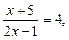 звідки
звідки 
Наносимо відповідні точки на числову вісь (див. рисунок).

Розглядаємо кожний з утворених інтервалів окремо.
1. Підставляємо значення  з інтервалу
з інтервалу 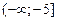 у нерівність (3). Дістаємо нерівність
у нерівність (3). Дістаємо нерівність 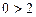 , яка не виконується. Тому нерівність (3) не виконується в усіх точках інтервалу
, яка не виконується. Тому нерівність (3) не виконується в усіх точках інтервалу 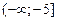 .
.
2. Підставляючи в нерівність (3) значення  з інтервалу
з інтервалу 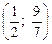 , дістаємо правильну нерівність
, дістаємо правильну нерівність  . Отже, нерівність (3) виконується на інтервалі
. Отже, нерівність (3) виконується на інтервалі 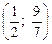 .
.
3. Підставляючи в (3) значення  з інтервалу
з інтервалу 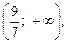 дістаємо неправильну нерівність
дістаємо неправильну нерівність  . Це означає, що нерівність (3) не виконується ні в одній точці інтервалу
. Це означає, що нерівність (3) не виконується ні в одній точці інтервалу  .
.
Остаточно маємо розв’язок нерівності (3)  .
.
9.6. Показникові нерівності
Розв’язування показникових нерівностей зводиться до розв’язування нерівності виду

Якщо 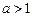 , то
, то 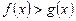 .
.
Якщо 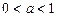 , то
, то 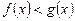 .
.
Приклад. Розв’язати показникову нерівність

Ø Переходячи до основи 3, дістаємо:
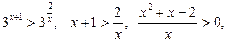
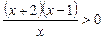 .
.
Розв’язавши останню нерівність методом інтервалів, знайдемо розв’язок 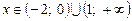 .
.
Приклад. Розв’язати показникову нерівність
 .
.
Ø Запишемо нерівність у вигляді
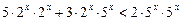 .
.
Поділивши обидві частини нерівності на 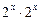 , дістаємо:
, дістаємо:
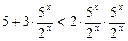 .
.
Позначивши  , дістанемо:
, дістанемо:
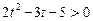 ,
, 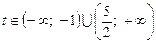 .
.
Розглядаємо два випадки:
1) 
2) 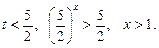
Остаточно маємо 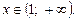
9.7. Логарифмічні нерівності
Розв’язання логарифмічних нерівностей зводиться до розв’язування нерівності виду
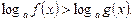 (1)
(1)
При цьому можливі два випадки:
1) якщо 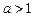 , то
, то 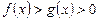 ;
;
2) якщо 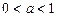 , то
, то 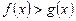 .
.
Приклад. Розв’язати нерівність
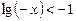 .
.
Ø Запишемо цю нерівність у вигляді (1):

звідки знайдемо розв’язок  або
або 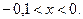
Приклад. Розв’язати нерівність
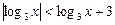 .
.
Ø Запишемо нерівність у вигляді
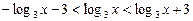 .
.
Звідси дістаємо:
 ,
,
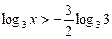 ,
, 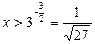 .
.
Найскладнішими є такі логарифмічні нерівності, в яких основи логарифмів залежать від х:
 (9)
(9)
Дістаємо дві системи нерівностей:
1)  2)
2) 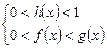 .
.
Об’єднання розв’язків цих систем і буде розв’язком нерівності (2).
|
|
|
Приклад. Розв’язати нерівність
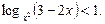
Ø Скориставшись співвідношенням 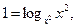 розв’яжемо дві системи нерівностей:
розв’яжемо дві системи нерівностей:
1)  2)
2) 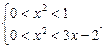
Шуканий розв’язок: 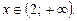
Приклад. Розв’язати логарифмічну нерівність
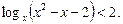
Ø Запишемо дану нерівність у вигляді (2):

Звідси дістаємо дві системи:
1)  2)
2) 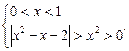
Побудуємо графік функції  .
.
При  маємо:
маємо:
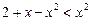 ,
, 
При  маємо:
маємо:
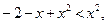
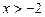 ,
, 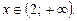
При  маємо:
маємо:
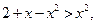
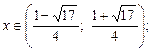
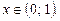
Розв’язок даної нерівності:  .
.
9.8. Деякі типові задачі вищої математики,
що зводяться до розв’язування системи нерівностей
Приклад. Знайти область існування функції
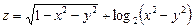 .
.
Ø Функція 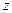 існує, якщо виконується система нерівностей:
існує, якщо виконується система нерівностей:

Нерівність вигляду 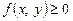 розв’язують, будуючи графік функції
розв’язують, будуючи графік функції 
Отже, будуємо графіки функцій 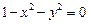 ,
,  і знаходимо область, де одночасно виконуються обидві нерівності (рис. 1). Коли йдеться про строгу нерівність, то відповідну межу позначаємо пунктиром. Шукану область заштриховуємо.
і знаходимо область, де одночасно виконуються обидві нерівності (рис. 1). Коли йдеться про строгу нерівність, то відповідну межу позначаємо пунктиром. Шукану область заштриховуємо.

Рис. 1.
Приклад. Знайти область існування функції
 .
.
Ø Функція існує, якщо виконується нерівність

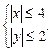
Шукану область зображено на рис. 2.
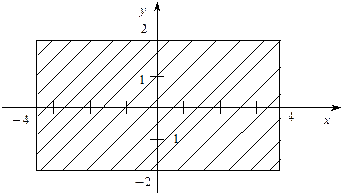
Рис. 2.
9.9. Тригонометричні
нерівності
Розв’язування будь-якої тригонометричної нерівності зводиться до розв’язування однієї з наведених далі шести нерівностей.
1. 
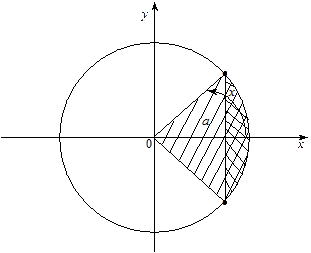
Рис. 1.
Із рис. 1 знаходимо розв’язок даної нерівності:
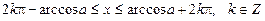 . (1)
. (1)
Приклад. Розв’язати нерівність

Ø Позначивши 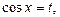 дістанемо квадратну нерівність:
дістанемо квадратну нерівність:
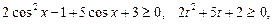

Повертаючись до початкових позначень, маємо:
 ;
;
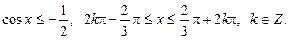
2. 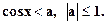
Із рис. 1 знаходимо розв’язок:
 . (2)
. (2)
Приклад. Розв’язати нерівність

Ø Позначивши  , дістанемо квадратну нерівність:
, дістанемо квадратну нерівність:
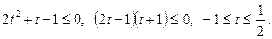
Повернувшись до початкових позначень, розв’яжемо нерівності:
1)  ;
;
2) 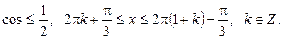
3. 
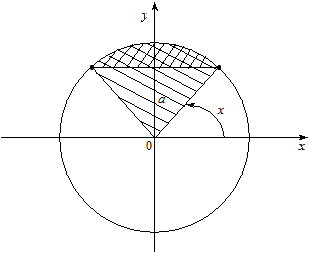
Рис. 2.
Із рис. 2 знаходимо розв’язок даної нерівності:
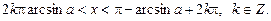 (3)
(3)
Приклад. Розв’язати нерівність
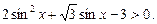
Ø Позначивши  розв’яжемо нерівність
розв’яжемо нерівність

Переходячи до початкових позначень, маємо:
1) 
2) 
4. 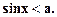
Із рис. 2 знаходимо розв’язок даної нерівності:
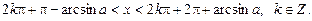 (4)
(4)
Приклад. Розв’язати нерівність
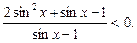
Ø Позначивши  розв’яжемо нерівність
розв’яжемо нерівність

Повертаюсь до початкових позначень, маємо:
|
|
|
1) 
2) 
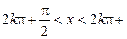
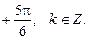
5. 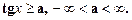

Рис. 3.
Із рис. 3 знаходимо розв’язок даної нерівності:
 (5)
(5)
Аналогічно розв’язується нерівність 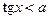 :
:
 . (6)
. (6)
Приклад. Розв’язати нерівність
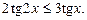
Виконавши заміну дістанемо
дістанемо
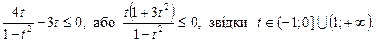
Повертаючись до початкових позначень, маємо:

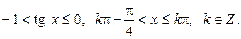
6. 

Рис. 4.
Із рис. 4 знаходимо розв’язок даної нерівності
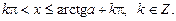 (7)
(7)
Аналогічно розв’язується нерівність 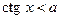 :
:
 . (8)
. (8)
Приклад. Розв’язати нерівність
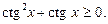
Ø Позначивши 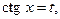 дістаємо
дістаємо 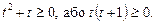
Повертаючись до початкових позначень, маємо:

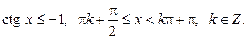
Приклад. Розв’язати нерівність

Ø Позначивши 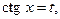 дістаємо нерівність:
дістаємо нерівність:
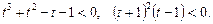
Повертаючись до початкових позначень, маємо:
1) 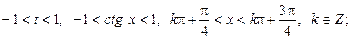
2) 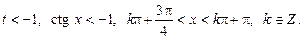
9.10. Алгебраїчні нерівності
Наведемо деякі відомі нерівності, часто використовувані під час розв’язування різних задач.
1. Нерівність Коші:
 (1)
(1)
2. Нерівність Гельдера
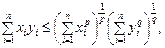 (2)
(2)
якщо 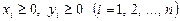 ;
; 
3.  якщо
якщо 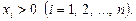 (3)
(3)
Приклад. Довести нерівність

Ø Якщо  , то нерівність, очевидно, виконується.
, то нерівність, очевидно, виконується.
Якщо  , підносимо обидві частини нерівності до квадрата:
, підносимо обидві частини нерівності до квадрата:

 . Нерівність доведено.
. Нерівність доведено.
Приклад. Довести, що для будь-якого трикутника зі сторонами  виконується нерівність
виконується нерівність
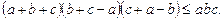
Ø Оскільки обидві частини нерівності додатні, то підносимо їх до квадрата:
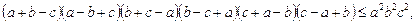

Оскільки  то нерівність доведено.
то нерівність доведено.
Приклад. Довести нерівність
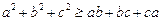 .
.
Ø Помноживши обидві частини нерівності на 2, дістанемо:
 звідки
звідки 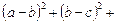
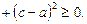
Остання нерівність, очевидно, виконується, що й доводить дану нерівність.
Приклад. Довести, що при будь-яких додатних значеннях а і b виконується нерівність

Ø Підносимо обидві частини нерівності до квадрата:


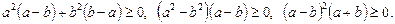
У результаті тотожних перетворень дістали правильну нерівність, що й доводить дану нерівність.
Приклад. Довести, що 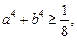 коли
коли 
Ø Узявши  розглянемо функцію
розглянемо функцію 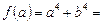
 Щоб відшукати мінімум функції
Щоб відшукати мінімум функції 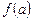 , знайдемо її похідну:
, знайдемо її похідну:
 .
.
З рівняння 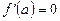 випливає:
випливає:
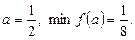
Отже, 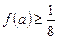 ,
, 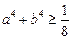 ,
, 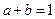 .
.
Якщо 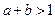 , то
, то 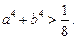
Приклад. Довести нерівність
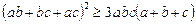 .
.
Ø Розкриваючи дужки, дістаємо:
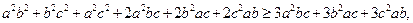
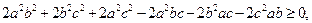
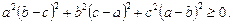
У результаті тотожних перетворень дістаємо нерівність, яка, очевидно, виконується, що й доводить дану нерівність.

1. Сформулюйте властивості нерівностей.
2. Як розв’язуються квадратні нерівності?
3. У чому полягає метод інтервалів?
4. Як розв’язуються ірраціональні нерівності?
5. Розв’язування показникових нерівностей.
6. Розв’язування логарифмічних нерівностей.
7. Розв’язування тригонометричних нерівностей.
Розв’язати нерівність (1—49).
1. 

2. 

3. 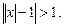
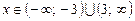
4. 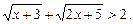
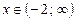
5. 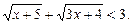
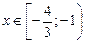
6. 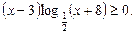

7. 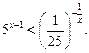
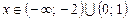
8. 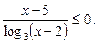

9. 

10. 
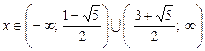
11. 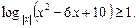
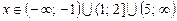
12. 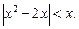

13. 
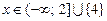
14. 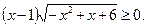
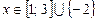
15. 
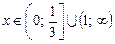
16. 

17. 

18. 

19. 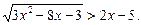

20. 
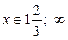
21. 
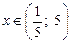
22. 

23. 

24. 

25. 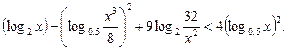

26. 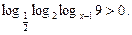

27. 

28. 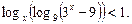

29. 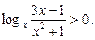

30. 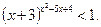
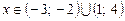
31. 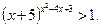
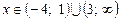
32. 

33. 

34. 

35. 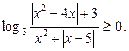
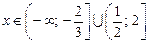
36. 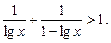

37. 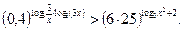
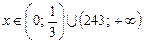
38. 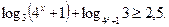

39. 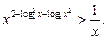
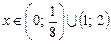
40. 

41. 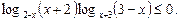

42. 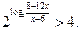
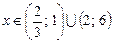
43. 

44. 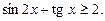

45. 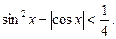
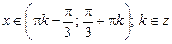
46. 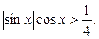

47. 

48. 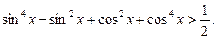
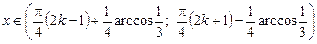
49. 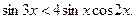
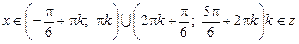
Довести нерівність (50—57).
50. 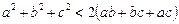 , якщо
, якщо  — сторони трикутника.
— сторони трикутника.
51. 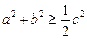 , якщо
, якщо  — сторони трикутника.
— сторони трикутника.
52.  , де
, де  — площа трикутника зі сторонами
— площа трикутника зі сторонами  .
.
53.  , де
, де  — площа трикутника зі сторонами
— площа трикутника зі сторонами  .
.
54. 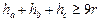 , де
, де  — висоти, опущені відповідно на сторони
— висоти, опущені відповідно на сторони  ;
; 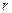 — радіус уписаного в трикутник кола.
— радіус уписаного в трикутник кола.
55.  , де
, де  ;
; 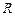 — радіус кола, описаного навколо трикутника;
— радіус кола, описаного навколо трикутника; 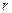 — радіус уписаного в нього кола.
— радіус уписаного в нього кола.
56. 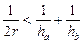 , де
, де 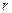 — радіус уписаного кола;
— радіус уписаного кола; 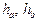 — висоти, проведені до сторін
— висоти, проведені до сторін  .
.
57. 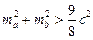 , де
, де  — медіани, проведені до сторін
— медіани, проведені до сторін  .
.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 459; Нарушение авторских прав?; Мы поможем в написании вашей работы!