Геометрические сплайны

С момента своего возникновения сплайны рассматривались как удобный инструмент в теории и практике приближения функций, в численных методах. С появлением компьютерной графики они получили широкое распространение и в этой области.

Термин "сплайн" происходит от английского spline гибкая полоска стали для проведения плавных кривых через заданные точки. В компьютерной графике сплайны используются для задания поверхности обтекаемого тела. В основе этого подхода к описанию поверхностей лежит использование сравнительно несложных формул, позволяющих восстанавливать облик изделия с необходимой точностью.

Достаточно типичной является следующая задача: по заданному массиву точек на плоскости (2D) или в пространстве (3D) построить кривую либо проходящую через все эти точки (задача интерполяции), либо проходящую вблизи от этих точек (задача сглаживания). При этом ограничимся лишь сплайнами, в построении которых используются кубические (в случае одномерных сплайнов - сплайновых кривых) и бикубические (в случае двумерных сплайнов - сплайновых поверхностей) многочлены. В компьютерной графике подобные сплайны применяются наиболее часто. Рассмотрим, прежде всего, что такое интерполяционный бикубический сплайн. Пусть на плоскости задан набор из (m+1)(n+1) точек (рис. 2)

Рис.2. Набор точек на плоскости

Добавим к каждой паре (xi, yj) третью координату zij (xi, yi, zij), т.е. получаем массив (xi, yi, zij), i=0,1,2,…,m; j=0,1,2,…,n. Прежде чем стоить поверхность, проходящую через все точки заданного массива, определим функцию, графиком которой будет эта поверхность.

Интерполяционным бикубическим сплайном называется функция двух переменных S(x, у), обладающая следующими свойствами:

1) график этой функции проходит через каждую точку заданного массива,
S(xi,yj) = zjj, i=0,l,...,m; j= 0,1,..., n;

2) на каждом частичном прямоугольнике
[xi, xi+l ] [yj. yj+1], i = 0, l,…,m-l, j = 0, l,...,n-l,

функция представляет собой многочлен третьей степени по каждой из переменных,

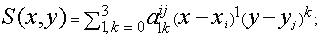
на всем прямоугольнике задания [x0, xm] [y0, yn] функция S(x, у) имеет по каждой переменной непрерывную вторую производную.

Для того чтобы построить по заданному массиву {(xi, yi, zij)} интерполяционный бикубический сплайн, достаточно определить все 16mn коэффициентов. Отыскание коэффициентов сплайн-функции сводится к построению решения системы линейных уравнений, связывающих искомые коэффициенты .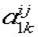

Последняя возникает из первого и третьего условий после добавления к ним недостающих соотношений путем задания значений производной искомой функции в граничных узлах прямоугольника [x0, xm] [y0, yn] (или иных соображений).

Достоинства преложенного способа для решения линейных систем, возникающих в ходе построения сплайн-функций, существует много эффективных методов, к тому же эти системы достаточно просты; графики построенных сплайн-функций проходят через все заданные точки, полностью сохраняя первоначально заданную информацию.
Вместе с тем изменение лишь одной точки (случай на практике довольно типичный) при описанном подходе заставляет пересчитывать заново, как правило, все коэффициенты.

К тому же во многих задачах исходный набор точек задается приближенно и, значит, требование неукоснительного прохождения графика искомой функции через каждую точку этого набора оказывается излишним.
От этих недостатков свободны некоторые из методов сглаживания.
Определим некоторые понятия, которые будут использованы в дальнейших рассуждениях.

Регулярной поверхностью называется множество точек M(x, y, z) пространства, координаты x, y, z которых определяются из параметрических уравнений поверхности

x = x(u, v), y = y(u, v), z = z(u, v), (u, v) D,
где x(u, v), y(u, v), z(u, v) гладкие функции своих аргументов, причем выполнено соотношение

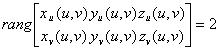
D некоторая область параметров на плоскости u и v.
Последнее равенство означает, что в каждой точке регулярной поверхности существует касательная плоскость и эта плоскость при непрерывном перемещении по поверхности текущей точки изменяется непрерывно.
Параметрические уравнения поверхности можно также записать в векторной форме:

r = r(u, v), (u, v) D,
где r(u, v) = (x(u, v), y(u, v), z(u, v)).
Для простоты будем считать, что область на плоскости параметров представляет собой стандартный единичный квадрат.
Ограничимся рассмотрением наборов точек вида Vij, i=0,l,...,m; j= 0,1,..., n. Соединяя соответствующие вершины прямолинейными отрезками, получаем контрольный (или опорный) граф заданного массива V (рис.2).

Сглаживающая поверхность строится относительно просто, в виде так называемого тензорного произведения. Так принято называть поверхности, описываемые параметрическими уравнениями вида

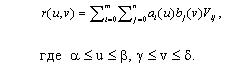
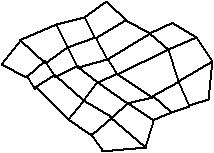
Рис.2. Контрольный граф

Построение сглаживающих поверхностей удобно начать с описания уравнений элементарных фрагментов.
Ограничившись бикубическим случаем (наиболее часто используемым в компьютерной графике), когда функциональные коэффициенты ai(u) и bj(v) представляют собой многочлены третьей степени относительно соответствующих переменных (кубические многочлены), запишем для заданного набора из 16 точек Vij, i= 0, l, 2, 3; j = 0, 1, 2, 3 параметрические уравнения элементарных фрагментов некоторых поверхностей, считая для простоты, что область изменения параметров u и v представляет собой единичный квадрат.
В зависимости от типа имеющихся исходных данных, от геометрии проектирующей поверхности применяют представления в виде форм:

• Эрмита;
• Безье;
• Бета-сплайнов (В-сплайнов).

Первый способ предполагает построение бикубического участка в виде изогнутого четырехугольника, к углам которого могут пристыковываться такие же участки и по Эрмиту имеющие вид:

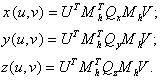
Здесь Mh матрица размерностью 4х4 имеет вид:

Матрицы Q размером 4х4 строятся на основе информации координат угловых точек по частным производным в этих точках:

Аналогично можно записать матрицы Qy и Qz.

При переходе с одного куска поверхности к другому обеспечивается совпадение координат всех точек граничащих кривых и совпадение первых производных в этих точках. Недостаток метода заключается в сложности получения значений частных производных в угловых точках.
Параметрические уравнения фрагмента элементарной бикубической поверхности Безье имеет вид:

В матричной форме выражение примет вид:

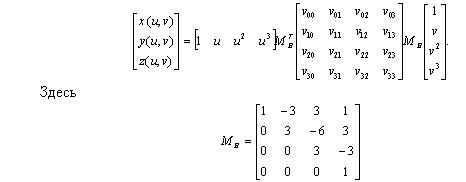
базисная матрица Безье.

Элементарная бикубическая поверхность Безье обладает следующими свойствами:
лежит в выпуклой оболочке порождающих ее точек;
является гладкой поверхностью;
опираясь в точки v00, v03, v30, v33, касается исходящих из них отрезков контрольного графа (рис.3).

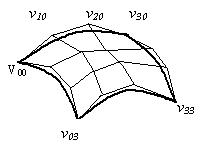
Рис.3. Пример поверхности Безье

Для гладкого перехода от одного элементарного бикубического элемента Безье к другому необходимо совпадение четырех смежных управляющих точек и отсутствие изломов в стыке соприкасающихся полей.
Существенным недостатком метода является то, что изменение местоположения хотя бы одной точки приводит к значительным изменениям вида всей кривой.
Матричное представление элементарного фрагмента бикубической В-сплайновой поверхности имеет вид:

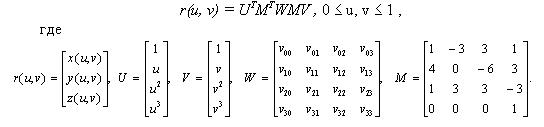
Элементарная бикубическая В-сплайновая поверхность имеет много положительных свойств:

является гладкой;

лежит в выпуклой оболочке порождающих ее 16 вершин;

повторяет контрольную многогранную поверхность;

обладает непрерывностью первой и второй производной, поэтому ее применяют для поверхностей со сложной топографией.

Дата добавления: 2014-01-15