Поведение гировертикали в режиме прямолинейного полета без маневрирования

Имеем следующую систему линеаризованных прецессионных уравнений движения ГВ для случая горизонтального полета с маневрированием по скорости и курсу

(1)

(2)

В режиме прямолинейного полета самолета без маневрирования имеем:

,

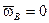
В силу этого в уравнениях (1) и (2) . Тогда (1) и (2) примут вид:

(3)

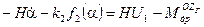(4)

Рассмотрим случай радиальной пропорциональной коррекции, то есть:

Тогда уравнения движения ГВ в режиме прямолинейного полета без маневрирования примут вид:

(5)

(6)

Решим данную систему линейных неоднородных дифференциальных уравнений первого порядка при следующих начальных условиях:

(7)

Введем обозначения:

, (8)

Здесь , - постоянные времени цепей коррекции.

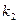Перепишем выражения (5) и (6) с учетом обозначений (8), поделив обе части уравнений (5) и (6) на и соответственно:

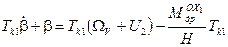(9)

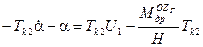(10)

Обозначим ;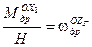

,- угловые скорости дрейфа ГВ относительно соответствующих осей. Подставим их в (9), (10):

(11)

(12)

Данные уравнения являются окончательно линеаризованными уравнениями движения ГВ в режиме прямолинейного полета без маневрирования. Их правая часть - очень медленно меняющаяся функция времени. Примем ее постоянной величиной. Ищем решение линейных неоднородных дифференциальных уравнений (11), (12) в виде:

,

где , - общие решения однородных дифференциальных уравнений, соответствующих данным неоднородным;

, - частные решения исходных неоднородных уравнений.

Ищем и в виде (в соответствии с корнями характеристического уравнения ):

,

Частные решения , подбираем по виду правой части:

;

Таким образом, решения системы дифференциальных уравнений (11), (12) имеют вид:

(13)

(14)

Найдем константы интегрирования в (13), (14), используя начальные условия (7):

, значит

, значит ;

Подставив , в уравнения (13), (14), получим окончательный вид решения системы дифференциальных уравнений, заданных (11) и (12):

(13)

(14)

Анализ полученного решения:

1) исследуем задачу статики, то есть поведение гировертикали при .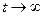

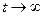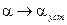
При , (- установившиеся значения углов и - статические погрешности). Наличие этих отклонений обеспечивает слежение вектора кинетического момента за вращающейся местной вертикалью.

,

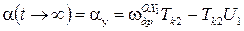Таким образом, уравнения (13), (14) можно переписать в виде:

(15)

(16)

Представим в виде составляющих:

, ;

где , 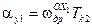- парциальные составляющие от действия моментов дрейфа;

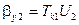, - парциальные составляющие, обусловленные вращением Земли (скоростные девиации -погрешности);

- скоростная девиация, обусловленная облетом Земли.

Данные статические погрешности являются основой для выбора крутизны коррекции. В этом случае считаем значение модуля вектора заданным, значение можно оценить конструктивно, остается определить, чему равны значения коэффициентов и 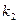. Для этого используется следующие условия:

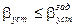, где 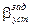- предельно допустимое значение погрешности по углу ;

, - предельно допустимое значение погрешности по углу .

Таким образом

и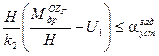

Из этих неравенств находим, чему равны коэффициенты , .

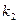При проектировании любой системы расчет может вестись:

а) на наихудший случай – погрешности максимальны, все их составляющие одного знака. Этот случай маловероятен

и

б) на среднестатистический случай. В таком случае выбор знаков погрешностей зависит от специфики работы ГВ в каждом отдельном случае.

Рассмотрим, чему могут быть равны 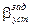, . Если в качестве МЧЭ используется ДЖМ, то заданные значения погрешности должны быть равны половине зоны пропорциональности ДЖМ (рабочей зоны) - .

;

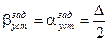В среднем у ДЖМ 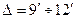, поэтому

Кривые восстановления ГВ:

Кривые восстановления показывают поведение ГВ на картинной плоскости. Для их составления необходимо исключить время из уравнений (15), (16):

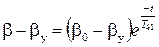(17)

(18)

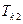Возведем левую и правую части уравнений (17), (18) в степени и соответственно:

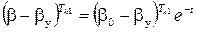(19)

(20)

Из уравнений (19), (20) следует:

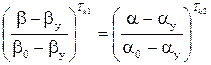(21)

Очевидно, что

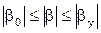, . (22)

Кривые восстановления могут различаться в зависимости от начальных условий. Рассмотрим случай равноэффективной коррекции, то есть когда . Значит, выполняется равенство . Тогда (21) можно переписать в виде:

(23)

С учетом неравенств (22) для различных соотношений знаков , кривые восстановления, описываемые уравнением (23), будут иметь вид:

На рис.1:

1 – кривая восстановления при , ;

2 – кривая восстановления при , ;

3 – кривая восстановления при , ;

4 – кривая восстановления при , ;

Дата добавления: 2014-01-15