Математические основы циклических кодов

Примеры кодов Хэмминга, обнаруживающих две ошибки и исправляющих одну ошибку

Десятичный эквивалент	Позиции, разряды и обозначения кода Хэмминга	mдоп
		2^3		2^2	2^1	2^0
т 1	m 2	k 4	m 3	k 3	k 2	k 1
							I
			I

2. Имеется единичная ошибка. В таком случае проверка на чётность расширенной кодовой комбинации показывает наличие ошибки (сумма единиц по модулю 2, входящих в кодовую комбинацию, не дает нуль). Декодирование по проверочной таблице без разряда m_доп указывает на номер искаженного символа, который нужно заменить на противоположный.

3. Имеются две ошибки. Проверка на чётность расширенной кодовой комбинации указывает на отсутствие ошибок, а декодирование по проверочной таблице – на наличие ошибки. В результате декодирования указывается номер позиции, где якобы возникла ошибка, однако её не следует исправлять, а лишь констатировать наличие двух ошибок).

Добавление дополнительного контрольного символа m_доп к закодированной для исправления одиночной ошибки кодовой комбинации увеличивает кодовое расстояние с d =3до d =4, так как r = 2, s = 1, а d = 2 + 1 + 1=4.

4.7.2. Циклические коды

Эти коды широко применяются в аппаратуре передачи данных и системах телемеханики благодаря высокой эффективности [9]. Простота аппаратной реализации на регистрах сдвига и ячейках сумматора по модулю два в своё время обеспечила им широкое применение, а сравнительно небольшая избыточность делает их эффективными в настоящее время.

Кодовая комбинация имеет информационные и контрольные разряды, последние помещаются в конце комбинации, т.е. коды являются систематическими, равномерными, обозначаются (n, k), где n – полное число разрядов, k – число информационных разрядов. Информационной частью служит натуральный двоичный код.

Кодовая комбинация представляется в виде многочлена (полинома) с фиктивной переменной x.

G (x) = a_{n -1} x^{n -1} + a_{n -2} x^{n -2} +... + a ₁ x + a ₀ x ⁰,

где коэффициенты а_i, i =0, 1, 2, … n -1 принимает значения 0 или 1.

Если а_i = 0, то этот член опускается.

Многочлен G (x) легко переводится в двоичный код. Например,

G (x) = x ⁷ + x ⁵ + x ³ + x ² + 1→10101101.

Если многочлен G (x)имеет старшую степень 7, то он называется многочленом 7-й степени.

Над многочленами можно выполнять математические действия по определенным правилам.

Сложение и вычитание равносильны и выполняются по mod 2.

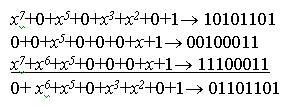
Умножение многочлена на x повышает степень каждого слагаемого многочлена на 1, умножение на хⁿ повышает степень каждого слагаемого на n. Это соответствует передвижению кодовых комбинаций на одну или «n» позиций в сторону старшего разряда.

Например, (х ³+ х +1) х ³= х ⁶+ х ⁴+ х ³ → 1011000.

В двоичном коде произведение получается из умножаемого двоичного числа приписыванием к нему справа количества нулей, равного величине степени «n».

Умножение многочлена на многочлен выполняется по правилам алгебры, при этом операция сложения выполняется по mod 2.

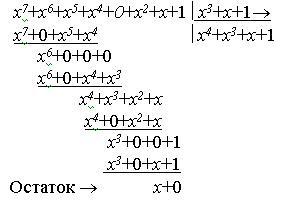
Деление многочлена на многочлен выполняется по правилам алгебры, при этом операция вычитания равносильна сложению по mod 2. Деление производится до тех пор, пока степень остатка не станет меньше степени делителя (число разрядов остатка меньше числа разрядов делителя).

Среди множества многочленов существуют неприводимые, которые не могут быть представлены в виде произведения многочленов низших степеней. Они аналогичны простым числам, которые делятся без остатка лишь сами на себя и на 1.

Для построения многочлена F (x) циклического кода производят следующие преобразования и операции:

1. Многочлен G (x) информационной части умножают на x^n-k; при этом степень многочлена G (x) повышается на величину «n - k».

2. К произведению (x^n-k)*(G (x)) добавляют остаток R (x) от деления x^n-k * G(x) на образующий многочлен P (x).

Это вытекает из следующих преобразований:

, (4.7)

где Q (x)– частное от деления без учета остатка, R (x) – остаток от деления, степень которого меньше степени P (x).

Умножая равенство (4.7) на P (x) получим:

x^n-K * G (x)= Q (x) * P (x) +R (x).(4.8)

Здесь Q (x) *P (x) =F (x) – искомый многочлен циклического кода, поэтому

F (x)= x^n-K * G (x)+ R (x), (4.9)

знак (-) заменен на (+), так как сложение выполняется по mod 2.

Дата добавления: 2014-01-20