Плоские волны и теория их распространения

Лекция №13

Различают плоские, цилиндрические и сферические волны. Наиболее распространенными являются сферические волны, распространяющиеся от источника, который условно можно считать точечным, если расстояние до него является значительно большим его размеров. Цилиндрические волны возбуждаются линейным проводом (теоретически бесконечным). Плоские волны являются некоторой идеализацией. Плоской волной можно приближенно считать и участок сферической и участок цилиндрической волны, если размеры этого участка значительно меньше расстояния до источника излучения. Обычно принимаемые поля регистрируются в сравнительно небольших областях пространства и в этих областях фронт любой волны, пришедший со сравнительно большой дальности, можно считать плоским. Плоские волны являются наиболее простыми и для их описания удобно пользоваться декартовой системой координат.

Так как вектор Умова-Пойтинга определяется как векторное произведение векторов и

,

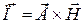и характеризует направление распространения волн, то векторы и колеблются в плоскостях, перпендикулярных направлению распространения.

Примем за направление распространения волн ось 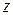. У плоской волны фронт ее распределения перпендикулярен направлению распространения и в плоскости этого фронта расположены векторы и . Такие волны называют поперечными. Очевидно, что в каждое мгновение значения и в плоскости фронта, т.е. в плоскости 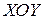постоянны и производные от них .

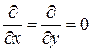Пусть среда является не проводящей, не имеет зарядов и ток проводимости в ней отсутствует. Тогда система уравнений Максвела практически симметрична относительно и и имеет вид

Запишем в координатной форме с учетом того, что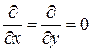

.

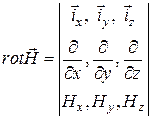
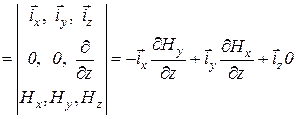Тогда первое уравнение Максвела в проекциях запишется так

, , .

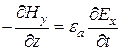Аналогично запишем и второе уравнение Максвела

, , .

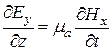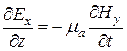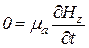Так как поле переменное во времени, то оно является переменным и в пространстве. А производная по времени от поля, изменяющегося во времени, равна нулю тогда, когда само поле равно нулю. Тогда из третьих уравнений в (13.3) и (13.4) следует, что 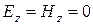. Т.е. поле имеет поперечный характер и вектора и изменяются лишь в плоскости перпендикулярной оси 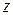. Из оставшихся уравнений (13.3) и (13.4) рассмотрим такие комбинации:

Из этих двух систем видно, что между собой попарно связаны независимыми системами уравнений (13.5) и (13.6) составляющие полей и 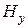, а также 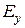и . Идентичные компоненты в них ортогональны друг другу и описывают независимые между собой волновые поля.

a)	б)

Рис. 13.1. Независимые волновые поля ортогональных поляризаций

Такие поля являются поляризованными. Направление поляризации обычно задают вектором . Первое из полей (рис. 13.1, а), поляризовано горизонтально, второе (рис. 13.1, б) имеет вертикальную поляризацию. Волны, соответствующие этим полям, имеют поперечный характер. В них вектора и взаимно перпендикулярны и колеблются в плоскости, перпендикулярной направлению распространения.

В дальнейшем достаточно рассмотреть одну из систем, например, систему а) (13.5).

Продифференцируем первое уравнение в (13.5) по времени

,

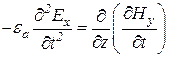и подставим в это уравнение выражение из второго уравнения (13.5).

Тогда получим

,

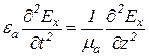или

,

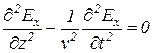где величина 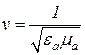имеет размерность скорости. Уравнения вида (13.8) называют волновыми.

Последнее уравнение можно записать так

,

или

,

где .

Решением этого уравнения в общем виде будет произвольные функции такого вида:

и ,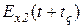

Именно для таких функций вторые производные по и будут равны между собой. Действительно, введя обозначение , найдем, например, вторые производные от функции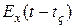

, ,

, .

Уравнению (13.9) будет удовлетворять не только функции (13.10), но и в более общем случае их сумма

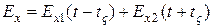
Такие функции называют волновыми, т.к. они описывают движущуюся волну (не обязательно гармоническую).

Время запаздывания в функции соответствует задержке во времени волны до появления ее в точке 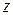. Скорость этой волны равна

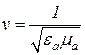
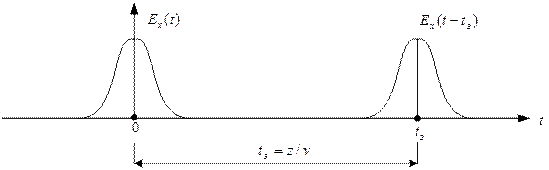
Рис. 13.2. Движущиеся волны как функции
пространственной координаты z и времени t

Функция 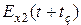описывает волну движущуюся в обратном направлении.

Рассчитаем скорость движения электромагнитной волны в "пустом" пространстве, т.е. в вакууме,

.

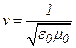Подставляя значения и , равные , , 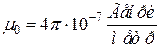в формулу (13.12), получим

Т.е. скорость распространения электромагнитных волн в вакууме равна скорости света.

Теперь решим систему уравнений (13.5), относительно поля 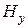. Продифференцируем второе уравнение (13.5) из этой системы по времени

,

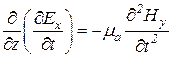и подставим в него выражение для из первого уравнения (13.5). В результате получим

,

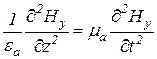или

,

где .

Решением будет сумма волн

,

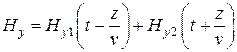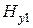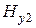где и - произвольные функции с запаздывающим аргументом .

Функции (13.11) и (13.14) связаны между собой уравнениями Максвела (13.5) и (13.6).

Чтобы найти эту связь подставим (13.11) и (13.14) в (13.5). Для простоты возьмем лишь первые слагаемые

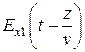и .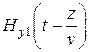

Обозначим 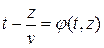. После подставки в уравнение (13.5) имеем:

,

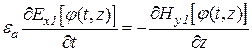или

,

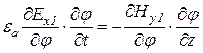где

, .

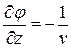Тогда

.

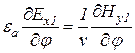Равенство (13.15) можно записать в виде

.

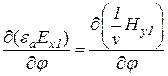Так как поле является переменным, то

,

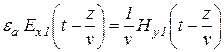или

Величину

называют волновым сопротивлением.

Суммарное решение для прямой и обратной волн равно

,

.

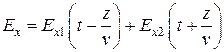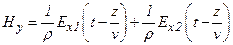Таким образом:

1. Плоские волны, являющиеся решениями уравнений Максвела, имеют поперечный характер. В них вектора и взаимно перпендикулярны и колеблются в плоскости, перпендикулярной направлению распространения.

2. Решение уравнения Максвела состоит из двух волн, прямой и обратной. В свободном пространстве обычно присутствует лишь прямая волна. Обратные волны появляются при наличии отражающих сред.

3. Скорость распространения волн 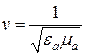. В вакууме .

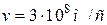4. Отношения , где - волновое сопротивление среды. Для вакуума. .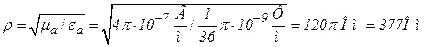

5. Количество энергии в электрическом и магнитном полях равны. Действительно 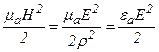. В сумме объемная плотность энергии

.

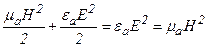За единицу времени через площадь проходит энергия сосредоточенная в объеме .

.

Эту же мощность можно подсчитать вычислив поток вектора Умова - Пойтинга.

,

где .

В частном случае волна имеет гармонический, т.е. синусоидальный или косинусоидальный характер.

,

.

В комплексной форме

.

Величину называют волновым числом.

С одной стороны

,

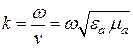с другой

,

где T - период колебаний, 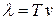- длина волны, рис. 13.3.

Рис. 13.3. Параметры гармонических волн

Вектора и 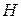колеблются во взаимно-перпендикулярных плоскостях.

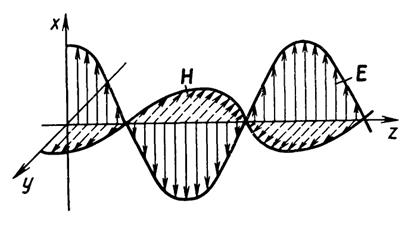
Рис. 13.4. Характер колебаний векторов и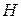

Дата добавления: 2014-01-20