
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема Гаусса-Маркова
|
|
|
|
Интервалы прогноза по линейному уравнению регрессии.
Качество уравнения регрессии. Коэффициент детерминации.
Анализ точности определения оценок коэффициентов регрессии.
Теорема Гаусса-Маркова.
Оценка качества уравнения регрессии.
Вопросы:
Вернемся к рассмотрению регрессионного уравнения 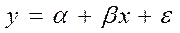 . Сделаем некоторые предположения.
. Сделаем некоторые предположения.
1) 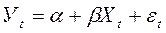 - спецификация модели, отражающая наше представление о механизме зависимости.
- спецификация модели, отражающая наше представление о механизме зависимости.
1) Хt – детерминированная экзогенная переменная. Случайный член должен быть распределен независимо от объясняющей переменной.
3) М(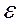 ) = 0, то есть случайный член не должен иметь систематического смещения. Это условие всегда можно выполнить, если модель включает свободный член, который будет учитывать любую систематическую тенденцию. Можно считать это условие выполняющимся автоматически.
) = 0, то есть случайный член не должен иметь систематического смещения. Это условие всегда можно выполнить, если модель включает свободный член, который будет учитывать любую систематическую тенденцию. Можно считать это условие выполняющимся автоматически.
D(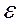 ) = M(
) = M(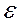 2) – M2(
2) – M2(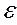 ) = M(
) = M(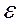 2) =
2) = 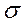 2 = Const для всех наблюдений. Условие независимости дисперсии от номера наблюдений называют гомоскедастичностью. Случай не выполнения условия гомоскедастичности называют гетероскедастичностью – M(
2 = Const для всех наблюдений. Условие независимости дисперсии от номера наблюдений называют гомоскедастичностью. Случай не выполнения условия гомоскедастичности называют гетероскедастичностью – M(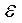 2) =
2) = 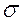 2
2 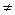 Const,
Const,
4) cov(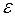 i,
i, 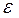 j) = M(
j) = M(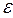 i
i 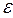 j) –M(
j) –M(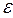 i)M(
i)M(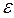 j) = M(
j) = M(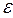 i
i 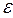 j) = 0. Предполагается отсутствие систематической связи между значениями
j) = 0. Предполагается отсутствие систематической связи между значениями 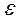 для разных наблюдений. Случайные члены должны быть независимыми. В случае, когда это свойство нарушается (временные ряды), говорят об автокорреляции остатков -
для разных наблюдений. Случайные члены должны быть независимыми. В случае, когда это свойство нарушается (временные ряды), говорят об автокорреляции остатков -
M(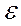 i
i 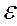 j)
j) 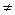 0.
0.
Часто добавляется условие 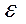 ~ N(0,
~ N(0, 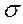 ). В этом случае модель называют нормальной линейной регрессионной моделью. Таки образом, задача состоит в оценке параметров
). В этом случае модель называют нормальной линейной регрессионной моделью. Таки образом, задача состоит в оценке параметров 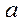 и
и 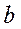 по данным наблюдений.
по данным наблюдений.
Теорема Гаусса-Маркова:
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 355; Нарушение авторских прав?; Мы поможем в написании вашей работы!