Свойства степенных рядов

Рассмотрим степенной ряд

имеющий радиус сходимости (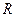может равняться 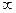). Тогда каждому значению 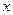из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от 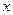на интервале сходимости. Обозначим ее через 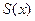. Тогда можно записать равенство

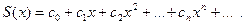
понимая его в том смысле, что сумма ряда в каждой точке 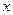из интервала сходимости равна значению функции 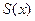в этой точке. В этом же смысле будем говорить, что ряд сходится к функции 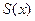на интервале сходимости. Вне интервала сходимости равенство не имеет смысла.

Пример 44 Найтисумму степенного ряда

Решение:

Это ряд составленный из членов геометрической прогрессии, у которой 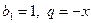. Следовательно, его сумма есть функция 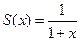. Ряд сходится, если 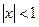. Поэтому равенство

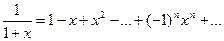
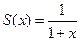справедливо лишь для значений , хотя функция определена для всех значений 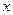кроме

Можно доказать, что сумма степенного ряда 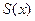непрерывна и дифференцируема на любом отроке 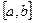внутри интервала сходимости.

Равенство справедливое в интервале сходимости степенного ряда называют разложением 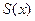в степенной ряд.

Для степенных рядов справедливы следующие утверждения:

1) Степенной ряд в интервале его сходимости можно почленно дифференцировать неограниченное число раз причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд а суммы их соответственно равны .

2) Степенной ряд можно неограниченное число раз почленно интегрировать в пределах от 0 до 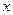, если 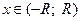, причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны

Дата добавления: 2014-01-11