Метод Эйлера решения задачи Коши для ОДУ 1-го порядка

В общем случае задача Коши решения в аналитическом виде не имеет, поэтому ее решают численными методами, простейшим из которых является метод Эйлера.

Для этого зададимся на оси 0x достаточно малыми шагами 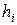. Будем рассматривать решение в точках с координатами (рис. 3.4.2):

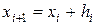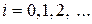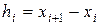, , . (3.4.3)

Введем обозначения:

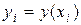; (3.4.4)

Из начального условия нам известно значение функции 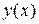в точке 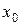: 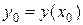. Для определения значения 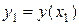в точке 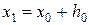запишем следующее равенство:

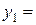
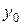
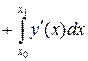(3.4.5)

Для проверки подставляем значение интеграла .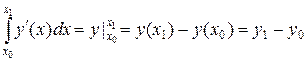

Рис. 3.4.2. Схема разбиения.

Далее, воспользуемся уравнением (3.4.1) и заменим под знаком интеграла на :

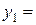
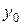
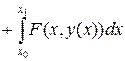(3.4.6)

Поскольку значение подынтегральной функции на интервале 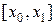нам известно только в точке 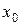, воспользуемся численным интегрированием по формуле левых прямоугольников:

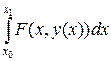
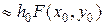(3.4.7)

Таким образом, приближенное значение 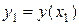можно получить по формуле

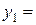
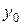
Аналогично можно получить приближенные значения:

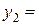
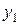
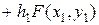
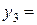
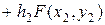
и т.д.

Пользуясь таким алгоритмом, последовательно получим решение для любого количества точек разбиения. Вышеизложенный подход для решения задачи Коши называется методом Эйлера. Общий вид метода Эйлера:

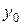– задано

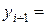
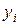
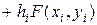(3.4.8)

Заметим, что в сложных практических случаях для решения применяются различные модифицированные алгоритмы, связанные с уточнением шага разбиения на каждом шаге пересчета. Среди такого рода модификаций наиболее употребляемыми являются методы типа Рунге-Кутта, излагаемые в соответствующей специализированной литературе. Приведем простейший вариант уточнения метода Эйлера.

Пусть значение 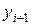, вычисленное по формуле (3.4.8) будет неокончательным (промежуточным). Обозначим его 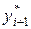, т.е.

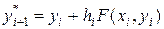(4.3.9)

Тогда для определения значения интеграла

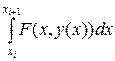
нам на интервале интегрирования 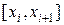известны значения подынтегральной функции в двух точках: 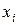и 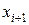. Поэтому можно воспользоваться формулой трапеции, которая на порядок точнее формулы левых прямоугольников:

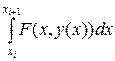
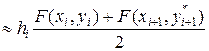(3.4.10)

Таким образом, общий вид уточненного алгоритма метода Эйлера имеет вид

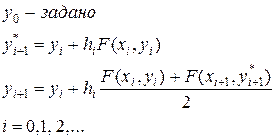(3.4.11)

Дата добавления: 2014-01-20